В случаях, когда применение оценок погрешностей в методах простых итераций и Зейделя невозможно из-за отсутствия констант 
или 
, ограничивающих сверху какие-либо нормы матрицы итерирования соответствующего метода (см. теоремы 6.2 и 6.6), эти методы неэффективны и, более того, как будет показано в параграфе 6.7, малонадежны ввиду медленной сходимости. Рассмотрим одно обобщение метода Зейделя, позволяющее иногда в несколько раз ускорить сходимость итерационной последовательности.
Пусть 
– обозначение 
-й компоненты 
-го приближения к решению системы (6.1) по методу Зейделя, а обозначение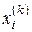 
будем использовать для -й компоненты -го приближения, получаемого новым методом. Этот метод определим равенством
(6.21)
где 
; 
, 
– задаваемые начальные значения; ω – числовой параметр, который называют параметром релаксации. Очевидно, при 
метод (6.21), называемый методом релаксации (ослабления), совпадает с методом Зейделя.
Конкретизируем метод релаксации для случая, когда исходная система (6.1) представляется в виде (6.7) и, следовательно, метод Зейделя имеет вид (6.13).
Пользуясь введенными здесь обозначениями, запишем на основании (6.13) дополнительное к (6.21) равенство для выражения компонент векторов 
через компоненты векторов 
(6.22)
Таким образом, метод релаксации можно понимать как поочередное применение формул (6.22) и (6.21) при каждом . Действительно, задав начальные значения 
и параметр 
, при 
, полагая вычислим
при 
, так же полагая , находим
и т.д. Но можно избавиться от вспомогательной последовательности 
, подставив (6.22) в (6.21). Для будем иметь:
(6.23)
От формулы (6.23), объединяющей формулы (6.22) и (6.21) и пригодной для проведения покоординатных вычислений, мало отличающихся от вычислений по методу Зейделя, легко перейти к векторно-матричной записи процесса релаксации. с этой целью перепишем (6.23) в виде
и далее, учитывая аддитивное представление матрицы 
, получаем векторно-матричный итерационный процесс в неявной форме
Умножив последнее равенство слева на матрицу 
, приходим к эквивалентному (6.23) методу простых итераций
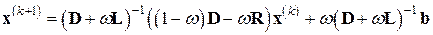(6.24)
(подстановка сюда значения превращает (6.24) в МПИ (6.14), эквивалентный методу Зейделя (6.13)).
Представление метода релаксации (6.23) в виде (6.24) позволяет сделать для него некоторые утверждения о сходимости, на основании соответствующих теорем о сходимости МПИ. Например можно применить теоремы 6.1 и 6.2, полагая в них 
, правда, получаемые при этом результаты вряд ли будут вызывать интерес. Более глубокие результаты на этом пути получают, изучая спектральные свойства таких матриц 
. Так, установлено, что сходимости процесса (6.23) необходимо, чтобы 
. Для некоторых классов СЛАУ (6.1) это требование к параметру релаксации является и достаточным. Справедлива следующая теорема, обобщающая теорему 6.8.
Теорема 6.12 (Островского-Рейча). Для нормальной системы 
метод релаксации (6.23) сходится при любом 
и любом .
Поскольку итерационный процесс (6.23) содержит параметр, естественно распорядиться им так, чтобы сходимость последовательности 
была наиболее быстрой. Очевидно, это достигается в том случае, когда спектральный радиус матрицы будет минимальным. В общем случае задача нахождения оптимального значения 
не решена, и в практических расчетах применяют метод проб и ошибок. Однако для отдельных важных классов задач такие значения удается выразить через собственные числа матрицы ( т.е. корни уравнения, фигурирующего в теореме 6.4 ) и даже оценить ускорение, достигаемое введением в процесс Зейделя оптимального параметра релаксации. Существенно отметить, что это оптимальное значение 
.При значениях 
метод (6.23) называют методом последовательной верхней релаксации (сокращенно ПВР- или SOR- методом*). Ввиду низкой эффективности метода (6.23) при 
, называемого в этом случае методом нижней релаксации, название «метод ПВР» в последнее время относят ко всему семейству методов (6.23), т.е. для любых . При этом случай 
называют сверхрелаксацией.
Покажем возможный выигрыш при использовании метода ПВР на простейшем примере.
Пример. Для системы
с симметричной положительно определенной матрицей 
и очевидным решением 
выполним по три итерационных шага, начиная с 
, методами Якоби, Зейделя и ПВР соответственно по формулам
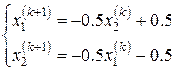
и
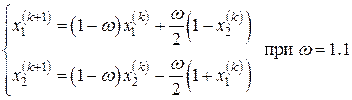
Сравнительные результаты третьего шага представлены следующей таблицей.
Таблица 6.1
| Метод Якоби | Метод Зейделя | Метод ПВР
(с  )
| |
| 0,875 | ≈0,969 | ≈1,0008 |
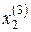
| −0,875 | ≈−0,984 | ≈−1,0009 |
| 0,125 | ≈0,031 | <0,001 |
Значение параметра релаксации ω здесь взято близким к оптимальному, которое для матриц «упорядоченных согласованно со свойством А» находится по формуле
где 
– спектральный радиус матрицы 
(в данном случае 
, 
, 
).
