Обратимся, наконец, к вопросам практической реализации итерационных методов решения линейных алгебраических задач.
Многие утверждения о сходимости итерационных процессов говорят о том, что решение поставленной задачи при определенных условиях может быть найдено этим процессом сколь угодно точно, причем погрешность каждого приближения может быть эффективно проконтролирована (см. теоремы 6.2, 6.6, 6.8, 6.12, а также теорему 6.3 и теорему 6.9). Нетрудно понять, что все это справедливо на самом деле лишь до тех пор, пока на погрешность метода (остаточную погрешность) не наложится вычислительная погрешность (погрешность округлений), неизбежная при любых реальных компьютерных расчетах. Особенно существенное и даже пагубное влияние на результат решения задачи итерационным методом могут оказать ошибки округления в тех случаях, когда утверждения о сходимости метода не содержат эффективных оценок погрешности (теоремы 6.1, 6.4, 6.5, 6.10, 6.12).
Рассмотрим различие между реальным и идеальным итерационными процессами на простейшем объекте – на методе простой итерации.
Пусть на 
-м итерационном шаге вычислений по методу (6.3) ошибки округлений составляют вектор 
. Тогда в отличие от идеального МПИ (6.3), генерирующего последовательность приближений 
к решению 
системы (6.1) такому, что
(6.41)
реальный МПИ будет иметь вид
(6.42)
Изучим поведение векторов
– ошибок приближений 
, получаемых реальным МПИ (6.42).
Вычитая (6.41) из (6.42), имеем
,
т.е.
(6.43)
Первое слагаемое в последнем выражении отвечает за погрешность идеального МПИ и может быть сделано сколь угодно малым в процессе итерирования при условии 
(см. лемму 6.1). Чтобы оценить второе слагаемое, предположим, что порог абсолютных погрешностей округлений, допускаемых на каждой итерации, есть 
, т.е.
Тогда
,
и, если 
, то второе слагаемое в (6.43), хотя и не стремится к нулю, но ограничено по норме величиной
При условии же , теоретически обеспечивающем сходимость идеального МПИ (6.3), малость этого второго слагаемого отнюдь не гарантируется, что означает допустимость ситуаций, когда в ходе реальных итераций погрешность округлений будет накапливаться вплоть до переполнения множества чисел, представляемых используемым компьютером.
Более детальный анализ влияния ошибок округления на итерационный процесс с попыткой пролить свет на природу этого влияния можно найти. Здесь же ограничимся напоминанием о том, что необходимо с осторожностью применять процессы, когда для них нет эффективных оценок погрешности, и по возможности, учитывать влияние ошибок округления, если такие оценки есть. Например, применительно к МПИ решения СЛАУ выше фактически доказана
Теорема 6.14. Пусть и приближения к решению системы (6.2) получаются посредством равенства (6.42), где – вектор ошибок округлений таких, что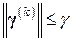 
. Тогда погрешность -го приближения при любом 
можно оценить неравенством
(6.44)
Действительно, для последовательности 
, получаемой МПИ (6.3), справедливо равенство
.
Следовательно, считая, что процессы (6.3) и (6.42) начинаются с одного начального приближения 
, в идентичном (6.43) равенстве
можно заменить 
на 
. Таким образом, погрешности 
-х приближений реального (6.42) и идеального (6.3) методов различаются лишь слагаемым, оцененным выше по норме величиной 
, т.е. и для процесса (6.42) можно воспользоваться оценкой, выведенной в теореме 6.2.
Отметим, что как непосредственно видно из оценки (6.44) (при значениях 
, приближающихся к единице), роль ошибок округлений в образовании общей погрешности тем сильнее, чем медленнее сходимость итерационного процесса.
