Метод Ньютона, его реализации и модификации

 

Пусть – некоторая последовательность невырожден­ных вещественных -матриц. Тогда, очевидно, последова­тельность задач

,

имеет те же решения, что и исходное уравнение (7.lа), и для приближенного нахождения этих решений можно формально записать итерационный процесс

, (7.5)

имеющий вид метода простых итераций (7.3) при . В случае это, как показано в конце предыдущего параграфа, – действительно МПИ с ли­нейной сходимостью последовательности . Если же различны при разных , то формула (7.5) определяет большое семейство итерационных методов с матричными параметрами . Рассмотрим некоторые из методов этого семейства.

Положим 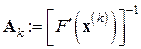, где

– матрица Якоби вектор-функции . Подставив это в (7.5), получаем явную формулу метода Ньютона

, (7.6)

обобщающего на многомерный случай скалярный метод Ньютона. Эту формулу, требующую обращения матриц на каж­дой итерации, можно переписать в неявном виде:

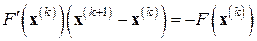. (7.7)

Применение (7.7) предполагает при каждом решение линейной алгебраической системы

относительно векторной поправки , а затем прибавление этой поправки к текущему приближению для получения следующего:

.

К решению таких линейных систем можно привлекать самые раз­ные методы как прямые, так и итерационные (см. гл. 2, 3) в зависимости от размерности решаемой задачи и специфики матриц Якоби (например, можно учитывать их симмет­рию, разреженность и т.п.).

Сравнивая (7.7) с формальным разложением в ряд Тейлора

,

видим, что последовательность в методе Ньютона получа­ется в результате подмены при каждом нелинейного уравнения 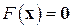или, что то же (при достаточной гладкости ), уравнения

линейным уравнением

,

т.е. пошаговой линеаризацией. Как следствие этого факта, можно рассчитывать, что при достаточной гладкости и достаточно хорошем начальном приближении сходимость порождаемой методом Ньютона последовательности к решению будет квадра­тичной.

Фактором, ос­ложняющим применение метода Ньютона к решению -мерных систем, является необходимость решения -мерных линейных задач на каждой итерации (обращения матриц в (7.6) или реше­ния СЛАУ в (7.7), вычислительные затраты на которые растут с ростом , вообще говоря, непропорционально быстро. Уменьше­ние таких затрат – одно из направлений модификации метода Ньютона.

Если матрицу Якоби вычислить и обратить лишь один раз – в начальной точке , то от метода Ньютона (7.6) придем к модифицированному методу Ньютона

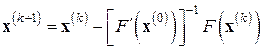. (7.8)

Этот метод требует значительно меньших вычислительных за­трат на один итерационный шаг, но итераций при этом может по­требоваться значительно больше для достижения заданной точ­ности по сравнению с основным методом Ньютона (7.6), по­скольку, являясь частным случаем МПИ (с ), он имеет лишь скорость сходимости геометрической прогрессии.

Компромиссный вариант – это вычисление и обращение матриц Якоби не на каждом итерационном шаге, а через несколько шагов (иногда такие методы называют рекурсивными).

Например, простое чередование основного (7.6) и модифи­цированного (7.8) методов Ньютона приводит к итерационной формуле

, (7.9)

где 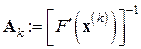, . За здесь принимается результат последовательного применения одного шага основно­го, а затем одного шага модифицированного метода, т.е. двух­ступенчатого процесса

(7.10)

Доказано, что такой процесс при определенных условиях порож­дает кубически сходящуюся последовательность .

Задачу обращения матриц Якоби на каждом -м шаге мето­да Ньютона (7.6) можно попытаться решать не точно, а прибли­женно. Для этого можно применить, например, итерационный процесс Шульца (см. § 6.6), ограничиваясь минимумом – всего одним шагом процесса второго порядка, в котором за начальную матрицу принимается матрица, полученная в результате преды­дущего -го шага. Таким образом, приходим к методу Ньютона с последовательной аппроксимацией обратных матриц:

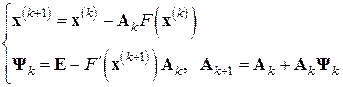, (7.11)

где , а и – начальные вектор и матрица соответственно. Этот метод (будем называть его более коротко ААМН – аппроксимационный аналог мето­да Ньютона) имеет простую схему вычислений – поочередное выполнение векторных в первой строке и матричных во второй строке его записи (7.11) операций. Скорость его сходимости поч­ти так же высока, как и у метода Ньютона. Последовательность может квадратично сходиться к решению уравнения 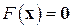(при этом матричная последова­тельность также квадратично сходится к , т.е. в нормально развивающемся итерационном процессе (7.11) должна наблюдаться достаточно быстрая сходимость к нулю).

Применение той же последовательной аппроксимации об­ратных матриц к простейшему рекурсивному методу Ньютона (7.9) или, что то же, к двухступенчатому процессу (7.10) опреде­ляет его аппроксимационный аналог

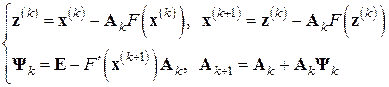, (7.12)

который, как и (7.9), также можно отнести к методам третьего порядка. Доказательство кубической сходимости этого метода требует уже более жестких ограничений на свойства и бли­зость к , к , чем в предыдущем методе. За­метим, что к улучшению сходимости здесь может привести по­вышение порядка аппроксимации обратных матриц, например, за счет добавления еще одного слагаемого в формуле для подсчета:

.

На базе метода Ньютона (7.6) можно построить близкий к нему по поведению итерационный процесс, не требующий вы­числения производных. Сделаем это, заменив частные производ­ные в матрице Якоби разностными отношениями, т.е. под­ставив в формулу (7.5) вместо матрицу , где

При удачном задании последовательности малых векторов (постоянной или сходящейся к нулю) по­лученный таким путем разностный (или иначе, дискретный) метод Ньютона

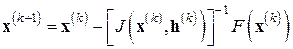(7.13)

имеет сверхлинейную, вплоть до квадратичной, скорость сходи­мости. При за­дании векторного параметра – шага дискретизации – следует учитывать точность машинных вычислений (macheps), точность вычисления значений функций , средние значения получаемых приближений.

Можно связать задание последовательности с какой­-либо сходящейся к нулю векторной последовательностью, например, с последовательностью невязок или поправок 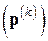. Так, полагая , где , а , приходим к простейшему методу секущих:

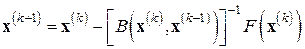(7.14)

где

,

Этот метод является двухшаговым и требует задания двух начальных точек и . При сходимость метода (7.14) имеет порядок . Можно рассчи­тывать на такую же скорость и в многомерном случае.

К методу секущих так же, как и к методу Ньютона, можно применить пошаговую аппроксимацию обратных матриц на ос­нове метода Шульца. Расчетные формулы этой модификации легко выписать, заменив в совокупности формул ААМН (7.11) матрицу на матрицу 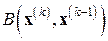из (7.14).

Замечание 7.1. Для останова процесса вычислений в быстросходя­щихся методах таких, как метод Ньютона, методы секущих и т.п., часто вполне успешно применяют простой критерий:

. (7.15)

Это можно объяснить двумя причинами. Во-первых, оценки погрешности здесь довольно «дороги». Имеется в виду как их получение (особенно для различных модификаций базовых методов), так и их реальное примене­ние. Во-вторых, в силу своей быстрой сходимости, к моменту достижения требуемой малости нормы поправки эти методы набирают такую инер­цию, что зачастую «проскакивают» установленный порог точности, т.е. выход по критерию (7.15) дает значение значительно (иногда на несколько порядков) меньшее, чем . Отслежи­вать факт сходимости в процессе итераций для того, чтобы реагировать на возможную расходимость в случаях, когда заранее не обеспечены условия сходимости применяемого метода, можно с помощью текущих проверок на уменьшение от шага к шагу поправок и невязок, т.е. выполнение нера­венств

и . (7.16)

 

МЕТОД БРАУНА

 

В отличие от пошаговой линеаризации векторной функции , приведшей к методу Ньютона (7.6), Брауном (1966 г.), предложено проводить на каждом итерационном шаге поочеред­ную линеаризацию компонент вектор-функции , т.е. линеа­ризовать в системе (7.1) сначала функцию 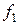затем и т.д., и последовательно решать получаемые таким образом уравнения. Чтобы не затенять эту идею громоздкими выкладками и лишни­ми индексами, рассмотрим вывод расчетных формул метода Брауна в двумерном случае.

Пусть требуется найти решение системы

, (7.17)

и пусть уже получены приближения , .

Подменим первое уравнение системы (7.17) линейным, по­лученным по формуле Тейлора для функции двух переменных:

.

Отсюда выражаем 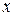(обозначим этот результат через ):

. (7.18)

При находим значение переменной :

,

которое будем считать лишь промежуточным приближением (т.е. не ), поскольку оно не учитывает второго уравнения системы (7.17).

Подставив в вместо 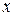переменную , придем к некоторой функции 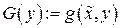только одной переменной . Это позволяет линеаризовать второе уравнение системы (7.17) с помощью формулы Тейлора для функции одной переменной:

. (7.19)

При нахождении производной нужно учесть, что есть сложная функция одной переменной , т.е. применить формулу полной производной

.

Дифференцируя по равенство (7.18), получаем выражение

,

подстановка которого в предыдущее равенство при , дает

.

При известных значениях 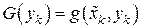и теперь можно разрешить линейное уравнение (7.19) относительно (назовем полученное значение ):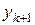

.

Заменяя в (7.18) переменную найденным значением 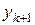при­ходим к значению :

.

Таким образом, реализация метода Брауна решения дву­мерных нелинейных систем вида (7.17) сводится к следующему.

При выбранных начальных значениях , 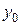каждое после­дующее приближение по методу Брауна находится при с помощью совокупности формул

,

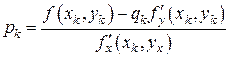
счет по которым должен выполнятся в той очередности, в кото­рой они записаны.

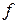Вычисления в методе Брауна естественно заканчивать, ко­гда выполнится неравенство с результатом ). В ходе вычислений следует контролировать немалость знаменателей расчетных формул. Заметим, что функции и в этом методе неравноправны, и перемена их ролями может изменить ситуацию со сходимостью.

Указывая на наличие квадратичной сходимости метода Брауна, отмечают, что рассчитывать на его большую по сравнению с методом Ньютона эффективность в смысле вычисли­тельных затрат можно лишь в случае, когда фигурирующие в нем частные производные заменяются разностными отношениями.

 

МЕТОД СЕКУЩИХ БРОЙДЕНА

 

Чтобы приблизиться к пониманию идей, лежащих в основе предлагаемого вниманию метода рассмотрим одномерный случай

В процессе построения методов Ньютона и секущих реше­ния нелинейного скалярного уравнения.

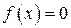(7.20)

функция в окрестности текущей точки подменяется ли­нейной функцией (аффинной моделью)

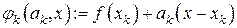(7.21)

Приравнивание к нулю последней, т.е. решение линейного уравнения

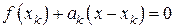
порождает итерационную формулу

(7.22)

для вычисления приближений к корню уравнения (7.20).

Если потребовать, чтобы заменяющая функцию вбли­зи точки аффинная модель имела в этой точке одинаковую с ней производную, то, дифференцируя (7.21), получаем значение коэффициента

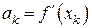
подстановка которого в (7.22) приводит к известному методу Ньютона. Если же исходить из того, что наряду с равенст­вом должно иметь место совпадение функций и в предшествующей точке т.е. из ра­венства

,

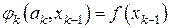или, в соответствии с (7.21),

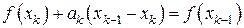, (7.23)

то получаем коэффициент

,

превращающий (7.22) в известную формулу секущих.

Равенство (7.23), переписанное в виде

,

называют соотношением секущих в . Оно легко обобща­ется на -мерный случай и лежит в основе вывода метода Брой­дена. Опишем этот вывод.

В -мерном векторном пространстве соотношение се­кущих представляется равенством

, (7.24)

где 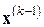, – известные -мерные векторы, – данное нелинейное отображение, а – некоторая матрица ли­нейного преобразования в . С обозначениями

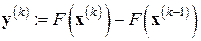, , (7.25)

соотношение секущих в обретает более короткую запись:

. (7.24а)

Аналогично одномерному случаю, а именно, по аналогии с формулой (7.22), будем искать приближения к решению векторного уравнения (7.1а) по формуле

. (7.26)

Желая, чтобы эта формула обобщала метод секущих, обра­тимую -матрицу в ней нужно подобрать так, чтобы она удовлетворяла соотношению секущих (7.24). Но это соотношение не определяет однозначно матрицу : глядя на равенство (7.24а), легко понять, что при существует множество матриц , преобразующих заданный -мерный вектор в другой заданный вектор .

При формировании матрицы будем рассуждать следующим образом.

Переходя от имеющейся в точке 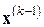аффинной модели функции

(7.27)

к такой же модели в точке

, (7.28)

мы не имеем о матрице линейного преобразования никаких сведений, кроме соотношения секущих (7.24). Поэтому исходим из того, что при этом переходе изменения в модели должны быть минимальными. Эти изменения характеризуют разность . Вычтем из равенства (7.28) определяющее ра­венство (7.27) и преобразуем результат, привлекая соотношение секущих (7.24). Имеем:

.

Представим вектор в виде линейной комбинации фиксированного вектора , определенного в (7.25), и некоторого вектора , ему ортогонального:

.

Подстановкой этого представления вектора в разность получаем другой ее вид

. (7.29)

Анализируя выражение (7.29), замечаем, что первое слагае­мое в нем не может быть изменено, поскольку

– фиксированный вектор при фиксированном . Поэтому ми­нимальному изменению аффинной модели будет отвечать случай, когда второе слагаемое в (7.29) будет нуль-вектором при всяких векторах , ортогональных векторам , т.е. следует находить из условия

. (7.30)

Непосредственной проверкой убеждаемся, что условие (7.30) бу­дет выполнено, если матричную поправку взять в виде одноранговой -матрицы

.

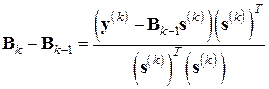Таким образом, приходим к так называемой формуле пересчета С. Бройдена (1965 г.)

, (7.31)

которая позволяет простыми вычислениями перейти от старой матрицы к новой такой, чтобы выполнялось соотноше­ние секущих (7.24а) в новой точке и при этом изменения в аф­финной модели (7.27) были минимальны (строго доказано, что такое построение отвечает минимальности поправки по норме Фробениуса на множестве матриц удов­летворяющих соотношению секущих (7.24а)).

Совокупность формул (7.26), (7.31) вместе с обозначениями (7.25) называют методом секущих Бройдена или просто методом Бройдена решения систем нелинейных числовых урав­нений.

Хотя в методах секущих обычным является задание двух начальных векторов , для метода Бройдена характер­но другое начало итерационного процесса. Здесь нужно задать один начальный вектор , начальную матрицу и далее в цикле по последовательно выполнять следующие операции:

1. решить линейную систему

(7.32)

относительно вектора (см. (7.26));

2. найти векторы и 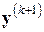(см. (7.25)):

, ; (7.33)

3. сделать проверку на останов (например, с помощью проверки на малость величин и/или ) и, если нужная точность не достигнута, вычислить новую матрицу по формуле (см. (7.31))

. (7.34)

В качестве матрицы , требуемой равенством (7.32) для запуска итерационного процесса Бройдена, чаще всего берут матрицу Якоби или какую-нибудь ее аппроксимацию. При этом, как отмечается, получаемые далее пересчетом (7.34) матрицы 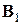, ,... не всегда можно считать близкими к соответствующим матрицам Якоби , ,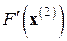... (что может иногда сыграть полезную роль при вырождении матриц ). Но, в то же время, показывается, что при определенных требованиях к матрицам Якоби матрицы обладают «свойством ограниченного ухудшения», означающим, что если и происходит увеличение с увеличением номера итерации , то достаточно медленно. С помощью этого свойства доказываются утверждения о линейной сходимости к при достаточной близости к и к , а в тех предположениях, при которых можно доказать квадратичную сходимость метода Ньютона (7.6), – о сверхлинейной сходимости последовательности приближений по методу Бройдена.

Как и в случаях применения других методов решения нели­нейных систем, проверка выполнимости каких-то условий схо­димости итерационного процесса Бройдена весьма затрудни­тельна и обычно заменяется проверками на выполнимость нера­венств типа (7.16).

Формуле пересчета (7.34) в итерационном процессе Брой­дена можно придать чуть более простой вид.

Так как, в силу (7.32) и (7.33),

,

а

,

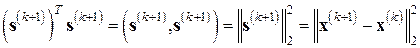то из формулы (7.34) получаем формально эквивалентную ей формулу пересчета

, (7.35)

которую можно использовать вместо (7.34) в совокупности с формулой (7.26) или с (7.32), (7.33) (без вычисления вектора 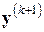). Такое преобразование итерационного процесса Бройдена несколько сокращает объем вычислений (на одно матрично­-векторное умножение на каждой итерации). Не следует, правда, забывать, что при замене формулы (7.34) формулой (7.35) может измениться ситуация с вычислительной устойчивостью метода; к счастью, это случается здесь крайне редко, а именно, в тех слу­чаях, когда для получения решения с нужной точностью требует­ся много итераций по методу Бройдена, т.е. когда и применять его не стоит.