Мы получили два эквивалентных определения определителя третьего порядка (формулы (4) и (5)). С помощью (4) определитель 3-го порядка вводится с помощью определителей второго порядка (разложение по столбцу). При этом легко проверяется, что все столбцы равноправны. Аналогично рекуррентным образом можно определить определитель n-го порядка (определитель квадратной матрицы n-го порядка), т.е.
=
= 
(7)
Но в этом случае уже не так просто, как для определителя третьего порядка, проверить, что разложения по остальным столбцам или строкам дают тот же самый результат. Поэтому чаще всего используют в качестве исходного другой подход к определению определителя n-го порядка. Но при этом используются в качестве вспомогательного материала перестановки и подстановки.
Пусть дан упорядоченный набор из n элементов. Элементы этого набора занумеруем числами 1, 2, 3, …, n. Очевидно, вместо того, чтобы говорить об элементах, можно говорить об их номерах.
Определение 4. Перестановкой из n чисел (или n символов) называется расположение этих чисел (или символов) в любом определённом порядке (без повторений).
Теорема 1. Число перестановок из n символов равно n!
Доказательство. Составляя перестановку, в качестве первого её элемента можно выбрать точно n символов. Если первый элемент выбран, то в качестве второго элемента можно выбрать любой из оставшихся (n – 1) символов. Следовательно, первые два места можно заполнить n×(n – 1) способами. Если два места в перестановке уже заполнены, то на третье место можно поставить любой из оставшихся (n – 2) символов. Следовательно, первые три места можно заполнить n×(n – 1)×(n – 2) способами. Продолжая этот процесс, получим, что все n мест в перестановке можно заполнить n×(n – 1)×(n – 2)×…×3×2×1 = n! способами.
Говорят, что числа к и р образуют в перестановке (… к…р…) инверсию, если к > р, но в перестановке к стоит раньше р. Перестановка называется чётной, если она содержит чётное число инверсий. Перестановка называется нечётной, если она содержит нечётное число инверсий.
Пример. 1) Перестановка (9, 7, 1, 3, 4, 8, 5, 2, 6) чётная. В ней число 9 образует инверсии со всеми стоящими за ней числами, их 8. Число 7 образует новые инверсии со всеми стоящими за ней числами, кроме числа 8, их 6. Число 1 не образует ни одной новой инверсии. Числа 3 и 4 образуют по одной новой инверсии с числом 2. Число 8 образует ещё инверсии с 5, 2 и 6, их 3. Число 5 образует инверсию с числом 2. Итак, получается 8 + 6 + 1 + 1 + 3 + 1 = 20 инверсий.
2) Перестановка (2, 1, 3, 5, 4, 6, 9, 8, 7) нечётная. В ней инверсии образуют пары чисел 2 и 1, 5 и 4, 9 и 8, 9 и 7, 8 и 7. Получилось 5 инверсий.
Если в перестановке два символа поменять местами, а все остальные символы оставить на старых местах, то получим новую перестановку. Это преобразование перестановки называется транспозицией.
Теорема 2. Всякая транспозиция меняет чётность перестановки.
Доказательство. Пусть в перестановке символы к и р меняются местами. При этом возможны два случая.
1) Символы к и р в данной перестановке стоят рядом, т.е. (… к, р …). После транспозиции получится перестановка (…. р, к …). Если к и р составляли инверсию в данной перестановке, то после инверсии они уже не будут составлять инверсию и наоборот. Число инверсий, которые к и р составляли в данной перестановке с остальными символами, не изменится. Следовательно, число инверсий изменится на 1, т.е. чётность перестановки изменится.
2) Символы к и р в данной перестановке стоят не рядом, т.е. (…. к,…,р…). После транспозиции получится перестановка (… р,…,к…). Число инверсий, которые к и р составляли в данной перестановке с символами, стоящими перед к и после р, не изменится. Если между к и р стоят m символов, то переставить к и р можно следующим образом: переставить к последовательно с каждым из этих m символов, затем переставить к и р, затем в обратном порядке переставить р с каждым из этих m символов. Получим 2m + 1 транспозиций соседних символов. По доказанному каждая из них меняет чётность перестановки. Итак, чётность перестановки изменилась.
Следствие. При n > 1 число чётных перестановок равно числе нечётных перестановок и равно 0,5×n!.
Определение 5. Подстановкой из n символов (или подстановкой n-ой степени) называется любое взаимнооднозначное отображение множества этих символов на себя.
Элементы данного множества будем обозначать 1, 2, …, n. Подстановка А может быть записана так: если число к переходит в число a к, то А = 
. Если в записи подстановки А некоторые столбцы поменять местами, то получится то же самое отображение данного множества, т.е. та же подстановка. Например,
А = = 
.
Запись подстановки А = будем называть стандартной. Всякую подстановку можно записать в стандартном виде. Верхнюю и нижнюю строки подстановки можно рассматривать как перестановки. Подстановка А называется чётной, если её верхняя и нижняя строки есть перестановки одинаковой чётности, т.е. общее число инверсий в них – чётное. В противном случае А называется нечётной. Так как перестановка столбцов равносильна транспозиции как в верхней так и в нижней строке, то при перестановке столбцов чётность подстановки не изменится, поэтому чётность подстановки можно вычислять по её стандартному виду и в этом случае она совпадает с чётностью нижней строки.
Подстановка Е = 
называется тождественной или единичной.
Произведением двух подстановок одного и того же порядка называется результат последовательного выполнения тех отображений, которые задают эти подстановки. Например, если А =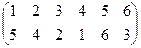 
, В = 
, то
А×В = 
. Действительно, первая подстановка переводит 1 в 5, вторая переводит 5 в 4, следовательно, окончательно 1 перейдёт в 4. Аналогично, 
, 
, следовательно, 
; 
, 
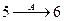, следовательно, 
; 
, 
, следовательно, 
; 
, 
, следовательно, 
; 
, 
, следовательно, 
.
Аналогично получаем, что В×А = 
. Отсюда следует, что умножение подстановок не подчиняется коммутативному закону. Но можно проверить, что (А×В) ×С = А× (В×С) для любых подстановок А, В, С одного и того же порядка. Очевидно, А×Е = Е×А для любой подстановки А, если А и Е одного порядка. Для подстановок А = и В = 
очевидно А×В = В×А = Е. Следовательно, А-1 = В, т.е. каждая подстановка имеет обратную.
Определители n-го порядка
Пусть А =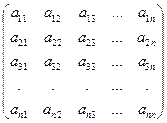 
произвольная квадратная матрица n-го порядка с действительными (или комплексными) элементами.
Определение 6. Определителем матрицы А (определителем n-го порядка) называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца. При этом произведение берётся со знаком «+», если подстановка из индексов входящих в него элементов чётная, и со знаком «-» в противном случае.
Обозначение определителя: | А | = 
.
Например, при n = 6 произведение а21а13а62а34а46а55 является членом определителя, так как в него входит точно по одному элементу из каждой строки и из каждого столбца. Подстановка, составленная из его индексов будет 
. В ней 4-е инверсии в верхней строке и 2-е инверсии – в нижней. Общее число инверсий равно 6, т.е. подстановка чётная. Следовательно, данное произведение входит в разложение определителя со знаком «+».
Произведение а21а13а62а34а46а15 не является членом определителя, так как в него входят два элемента из первой строки.
Свойства определителей.
10. При транспонировании определитель не меняется (напомним, что транспонирование матрицы и определителя означает перемену строк и столбцов местами).
Действительно, если (-1)к 
является членом определителя, то все a1, a2, …, an различны и к – число инверсий в перестановке (a1, a2, …, an). При транспонировании номера строк станут номерами столбцов и наоборот. Следовательно, в произведении все множители будут из разных столбцов и строк, т.е. это произведение будет входить в транспонированный определитель. Знак его будет определяться числом инверсий в подстановке . Но это число, очевидно равно к. Итак, (-1)к будет членом транспонированного определителя. Так как мы брали любой член данного определителя, а число членов в данном и транспонированном определителях одинаково, то отсюда и следует их равенство. Из доказанного свойства следует, что всё, что будет доказано для строк определителя, будет верно и для его столбцов.
20. Если все элементы строки (или столбца) определителя равны нулю, то определитель равен нулю.
Это следует из того, что по одному элементу указанной строки (или столбца) будет входить в каждый член определителя.
30. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя.
Действительно, если все элементы к-ой строки имеют общий множитель l, то их можно записать в виде 
. Любой член определителя будет иметь вид (-1)s 
. Следовательно, из всех членов определителя можно вынести множитель l.
40. Если две строки определителя поменять местами, то определитель сменит знак.
Действительно, если (-1)к 
любой член данного определителя, то в новом определителе номера строк р и q поменяются местами, а номера столбцов останутся прежними. Следовательно, в новом определителе это же самое произведение будет входить в виде (-1)s 
. Так как в номерах строк произошла одна транспозиция, а номера столбцов не изменились, то к и s имеют противоположные чётности. Итак, все члены данного определителя изменили знак, следовательно, и сам определитель изменил знак.
50. Если две строки определителя пропорциональны, то определитель равен нулю.
Действительно, пусть все элементы к-ой строки равны соответствующим элементам р-ой строки, умноженным на l, т.е. | А | = 
= 
= 0.
60. Если в определителе все элементы к-ой строки есть суммы двух слагаемых, то определитель равен сумме двух определителей, в которых все строки, кроме к-ой, такие же как и в данном определителе. На месте элементов к-ой строки одного из них стоят первые слагаемые элементов к-ой строки данного определителя, а на месте элементов к-ой строки второго – вторые их слагаемые.
Пусть элементы к-ой строки будут 
+ ск1, 
+ ск2, …., 
+ скn. Тогда любой член определителя будет иметь вид
(-1)s 
= (-1)s 
+ (-1)s 
.
Собрав все первые слагаемые, мы получим определитель, отличающийся от данного только к-ой строкой. На месте к-ой строки будут стоять , , …., . Собрав все вторые слагаемые, получим определитель тоже отличающийся от данного только к-ой строкой. В к-ой строке будут стоять ск1, ск2, …., скn.
70. Если к одной строке определителя прибавить другую его строку, все элементы которой умножены на одно и то же число, то определитель не изменится.
Это свойство является следствием двух предыдущих.
Если в определителе | А | вычеркнуть к-ую строку и р-ый столбец, то останется определитель (n–1)-го порядка. Он называется минором, дополнительным для элемента 
и обозначается Мкр. Число (-1)к+р×М кр называется алгебраическим дополнением для элемента и обозначается Акр.
80. Дополнительный минор и алгебраическое дополнение не зависит от того, какой элемент стоит в к-ой строке и р-ом столбце определителя.
Лемма 1 D = 
. (8)
Доказательство. Если а11 = 0, то равенство (8) очевидно. Пусть а11 ¹ 0. Так как в каждый член определителя входит точно один элемент из первой строки, то ненулевыми членами определителя могут быть только те, в которые входит а11. Все они имеют вид 
, где gк и к пробегают значения от 2 до n. Знак этого члена в определителе D определяется чётностью подстановки s = 
.Таким образом D есть алгебраическая сумма слагаемых вида со знаками, определяемыми подстановкой s. Если в этой сумме вынести за скобки а11, то получим, что D = а11× S, где S есть алгебраическая сумма слагаемых вида 
, знак которых определяется подстановкой s. Этих слагаемых, очевидно, (n – 1)!. Но подстановка s и подстановка 
имеют одинаковую чётность. Следовательно, S = М 11. Так как А11 = (-1)1+1× М 11 = М 11, то D = а11×А11.
Лемма 2. D = 
(9)
Доказательство. В определителе D переставим р-ую строку последовательно с каждой предыдущей. При этом р-ая строка займёт место первой строки, но минор, дополнительный к элементу арк не изменится. Всего будет сделано (р – 1) перестановка строк. Если новый определитель обозначить D1, то D = (-1)р-1×D. В определителе D1 переставим к -ый столбец последовательно с каждым предыдущим столбцом, при этом будет сделано (к – 1) перестановка столбцов и минор, дополнительный к арк, не изменится. Получится определитель
D2 =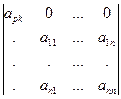 
. Очевидно, D2 = (-1)р-1×D1 = (-1)р+к-2×D = (-1)р+к×D. По лемме 1, D2 = арк×М рк. Отсюда D = арк× (-1)р+к × М рк = арк×Арк.
Теорема 3. Определитель равен сумме произведений элементов некоторой строки на их алгебраические дополнения, т.е. D = ак1Ак1 + ак2×Ак2 +…+аkn×Аkn (10).
Доказательство. Пусть D = 
. Элементы к-ой строки запишем в виде ак1 =ал1 + 0 + …+ 0, ак2 = 0 + ак2 + 0 + … + 0, …, а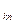 
= 0 + 0 + …+ 0 + а 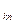. Используя свойство 60, получим, что D = 
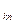= = ак1Ак1 + ак2Ак2 + … + а А 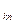(использовали лемму 2).
Теорема 4. Сумма произведений элементов одной строкиопределителя на алгебраические дополнения соответствующих элементов другой строки равна нулю.
Доказательство. Пусть D = 
. По предыдущей теореме
D = 
. Если взять 
, то в определителе Dбудет две одинаковые строки, т.е. D будет равен нулю. Следовательно, 0 = 
, если р ¹ к.
Замечание. Теоремы 3 и 4 будут верны, если в их формулировках слово «строка» заменить на слово «столбец».
Способ вычисления определителя n-го порядка.
Для вычисления определителя n -го порядка достаточно в какой-нибудь строке (или столбце) получить как можно больше нулей, используя свойство 70, а потом использовать теорему 3. При этом вычисление определителя n-го порядка сведётся к вычислению определителя (n – 1)-го порядка.
Пример. Вычислите определитель D = 
.
Решение. Получим нули во второй строке. Для этого второй столбец 1) умножим на (-2) и прибавим к первому столбцу; 2) прибавим к третьему столбцу; 3) умножим на (-4) и прибавим к четвёртому столбцу. Получим, что D = 
. Разложим полученный определитель по элементам второй строки. При этом произведения всех элементов этой строки на их алгебраические дополнения, кроме элемента 1, равны нулю. Для того, чтобы получить алгебраическое дополнение для элемента 1, нужно вычеркнуть те строку и столбец, где этот элемент стоит, т.е. вторую строку и второй столбец. Знак алгебраического дополнения определяет (-1)2+2 = (-1)4 = +1. Итак, D = + 
. Получили определитель 3-го порядка. Этот определитель можно вычислить, используя диагонали и треугольники, но можно свести к определителю второго порядка. Умножим первый столбец 1) на (-4) и прибавим ко второму столбцу, 2) умножим его на 2 и прибавим к третьему столбцу. Получим, что
D = 
. Следовательно, D = (-1)2+1 
. Используя свойство 70, прибавим к первому столбцу второй, получим D = - 
= -3×(23 – 40) = 51.
Некоторые определители (например, такие, в которых стоят «большие» миноры, целиком состоящие из нулей) удобно разлагать по нескольким строкам. Это позволяет делать теорема Лапласа. Пусть в определителе D выделен минор М s-го порядка, элементы которого стоят на строках с номерами к1,к2,…,кs и на столбцах с номерами р1,р2,…,рs. Вычеркнем строки и столбцы с указанными номерами. После этого останется определитель (n – s)-го порядка. Его называют минором М1, дополнительным к минору М. Если s = к1+…+ кs + р1+…+рs, то
алгебраическим дополнением к минору М называется А = ( -1)s× М1.
Теорема 5 (теорема Лапласа). Пусть в определителе n -го порядка выделены к строк (или столбцов). Определитель равен сумме произведений всех миноров, стоящих на выделенных строках, на их алгебраические дополнения.
Доказательство этой теоремы опустим.
Пример. 
= -(1 – 20)(28 + 6) = 19×34 = 661.
Теорема 6 (теорема Крамера). Если в системе линейных уравнений число неизвестных равно числу уравнений и определитель D системы отличен от нуля, то система имеет решение и только одно. Это решение получается по формулам 
, где каждое Dк получается из D заменой к-го столбца столбцом свободных членов.
Доказательство. Пусть дана система 
и D ¹ 0. Умножим первое уравнение на А1к, второе – на А2к, …,n- ое уравнение – на Аnк и все уравнения сложим. Получим 
+…... + 
+ … + 
= 
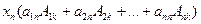Используя теоремы 3 и 4, получим х1 ×0 + … + хк ×D + … + хn ×0 = D к, где D к = 
(к-ый столбец в определителе D заменён столбцом свободных членов уравнений данной системы). Отсюда 
= 
для всех к = 1, 2, …, n.
III. МАТРИЦЫ
