Логическая формула – запись сложного высказывания в виде простых высказываний, соединенных операциями отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции и скобок.
В случае, если в логической формуле присутствуют несколько операций, не разделенных скобками, то порядок выполнения операций следующий:
1) отрицание;
2) конъюнкция;
3) дизъюнкция;
4) импликация;
5) эквиваленция.
Формула называется тавтологией, если она истинна при любых значениях истинности, входящих в нее высказываний.
Например, рассмотрим возможные значения истинности формулы 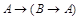 . Построим таблицу истинности для данной формулы.
. Построим таблицу истинности для данной формулы.
| А | В | 
| 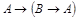
|
Формула всегда только истинна, значит является тавтологией.
Формула называется противоречием, если она ложна при любых значениях истинности, входящих в нее высказываний.
Например, рассмотрим возможные значения истинности формулы 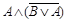 . Построим таблицу истинности для данной формулы.
. Построим таблицу истинности для данной формулы.
| А | В | 
| 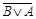
| 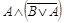
|
Формула всегда только ложна, значит является противоречием.
Формулы называются равносильными, если при любых значениях истинности высказываний, в них входящих, значения истинности формул совпадают.
Для обозначения равносильности формул используют знак  . Для выяснения равносильности формул для них строят таблицы истинности.
. Для выяснения равносильности формул для них строят таблицы истинности.
Например, доказать равносильность формул 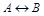 и
и 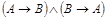 .
.
Отразим в таблице истинности значения истинности каждой формулы.
| А | В | 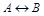
| 
| 
| 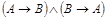
|
Значения истинности формул при одинаковых значениях истинности высказываний А и В совпадают (выделенные столбцы), что дает право утверждать равносильность формул, значит 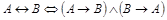 .
.
Аналогично можно показать, что имеют место следующие равносильности, которые называют законами логики:
1.  (закон двойного отрицания);
(закон двойного отрицания);
2. 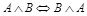 (закон коммутативности конъюнкции);
(закон коммутативности конъюнкции);
3. 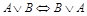 (закон коммутативности дизъюнкции);
(закон коммутативности дизъюнкции);
4. 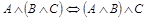 (закон ассоциативности конъюнкции);
(закон ассоциативности конъюнкции);
5. 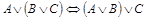 (закон ассоциативности дизъюнкции);
(закон ассоциативности дизъюнкции);
6.  (закон дистрибутивности конъюнкции относительно дизъюнкции);
(закон дистрибутивности конъюнкции относительно дизъюнкции);
7.  (закон дистрибутивности дизъюнкции относительно конъюнкции);
(закон дистрибутивности дизъюнкции относительно конъюнкции);
8.  (закон де Моргана);
(закон де Моргана);
9. 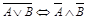 (закон де Моргана);
(закон де Моргана);
10. 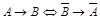 (закон контрапозиции);
(закон контрапозиции);
11. 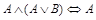 (закон поглощения);
(закон поглощения);
12. 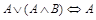 (закон поглощения);
(закон поглощения);
13. 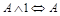 ;
;
14.  ;
;
15. 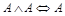 ;
;
16. 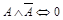 (закон противоречия);
(закон противоречия);
17.  ;
;
18. 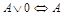 ;
;
19.  ;
;
20. 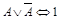 (закон исключенного третьего);
(закон исключенного третьего);
Предикаты и кванторы
Предикат – это предложение с переменными, которое после замены переменных определенными их значениями превращается в высказывание.
Если предикат содержит одну переменную х, то его обозначают  , если предикат содержит две переменные х и у, то его обозначают
, если предикат содержит две переменные х и у, то его обозначают 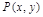 и т.д.
и т.д.
Например:
а)  : «х – четное число» является предикатом;
: «х – четное число» является предикатом;
б) любое уравнение или неравенство является предикатом.
Для предикатов аналогично определены те же операции, что и для высказываний.
Например:
а) система уравнений или неравенств – конъюнкция предикатов;
б) совокупность уравнений или неравенств – дизъюнкция предикатов.
Существуют 2 вида кванторов:
1) Квантор всеобщности. Обозначается 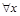 . Запись
. Запись 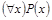 читается как «Для любого х выполняется Р(х)» или «Для всех х верно Р(х)» или «Для каждого х Р(х)».
читается как «Для любого х выполняется Р(х)» или «Для всех х верно Р(х)» или «Для каждого х Р(х)».
2) Квантор существования. Обозначается 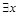 . Запись
. Запись 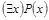 «Существует х, такое что
«Существует х, такое что 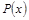 » или «Для некоторых х верно
» или «Для некоторых х верно 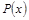 » или «Хотя бы один х
» или «Хотя бы один х 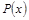 ».
».
Например:
Пусть 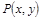 : «Официант х обслуживает стол у». Тогда
: «Официант х обслуживает стол у». Тогда
 означает«У любого официанта есть стол, который он обслуживает».
означает«У любого официанта есть стол, который он обслуживает».
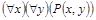 означает«Каждый официант обслуживает все столы».
означает«Каждый официант обслуживает все столы».
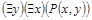 означает«Существует стол, который обслуживается некоторым официантом».
означает«Существует стол, который обслуживается некоторым официантом».
Для любого предиката 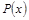 имеют место следующие равносильности:
имеют место следующие равносильности:
· 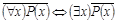 ;
;
·  .
.
Эти правила используются для построения отрицаний предложений.
Например:
Постройте отрицание предложения «Некоторые студенты нашего факультета не сдали сессию».
Решение: Р (х): «Студент х нашего факультета не сдал сессию». Тогда исходное предложение запишется как 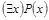 , а его отрицание как
, а его отрицание как  , что читается как «Все студенты нашего факультета сдали сессию».
, что читается как «Все студенты нашего факультета сдали сессию».
Упражнения
1. Какие из следующих предложений являются высказываниями:
а) Москва – столица России;
б) студент института физико-математического образования;
в) 5+3 – 6;
г) 12 – 6 + 1 = 100;
д) Джинсы удобнее брюк;
е) а>0;
ж) Кризис пошел на пользу РФ;
з) Да здравствует солнце, да скроется тьма!
и) В 2017 году будет 2017 дней;
к) Студент х сегодня опоздал на занятия;
л) Барнаул – центр Алтайского края?
м) В АлтГПА учатся 2013 студентов;
н) Желаю Вам удачи!
о) Здесь сейчас душно;
п) Луна есть спутник Марса;
р) Россия – великая держава.
2. Приведите примеры предложений, а) являющихся высказываниями; б) не являющихся высказываниями.
3. Прочтите формулу 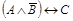 , если А – «У студентов сессия»; В – «Студенты ходят на занятия»; С – «Наступило лето».
, если А – «У студентов сессия»; В – «Студенты ходят на занятия»; С – «Наступило лето».
4. Установите, истинно или ложно высказывание:
а) «Если мама – это родитель, то папа – это логарифм»;
б) «Сегодня 21 октября, да и завтра – четверг»;
в) «Я студент или живу в РФ»;
г) «7 – простое число и не делится на 5»;
д) «В нашей группе есть студентка по имени Ольга тогда и только тогда, когда завтра выходной»;
е) «Если сегодня шел дождь, то я пришел на занятия»;
ж) «Число 212 делится на 3 и 4»;
з) «Завтра Новый год тогда и только тогда, когда сегодня - май»;
и) «45 кратно 3 или 12 не кратно 3»;
к) «Неверно, что я не студент».
5. Среди пар высказываний выберите те, которые являются отрицаниями друг друга:
а) «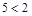 » и «
» и « »;
»;
б) «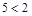 » и «
» и « »;
»;
в) «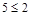 » и «
» и « »;
»;
г) «3 – положительное число» и «3 – отрицательное число»;
д) «3 – четное число» и «3 – нечетное число»;
е) «3 – положительное число» и «3 – неотрицательное число»;
ж) «3 – отрицательное число» и «3 – неотрицательное число»;
з) «Сегодня я пойду в кино» и «Сегодня я пойду в театр».
6. Определите значение истинности высказывания А, если следующие высказывания истинны:
а) 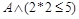 ;
;
б) 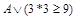 ;
;
в) Если А, то 4 – нечетное число;
г) А тогда и только тогда, когда 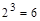 .
.
7. Определите значение истинности высказывания А, если следующие высказывания ложны:
а)  ;
;
б) 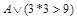 ;
;
в) Если 4 – четное число, то А;
г) 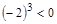 тогда и только тогда, когда не А.
тогда и только тогда, когда не А.
8. Будут ли справедливой равносильность:
а)  ;
;
б) 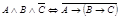 ;
;
в) 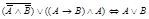 ;
;
г). 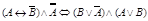 .
.
9. Родители сказали детям: «Если мы поедем летом в дом отдыха, то вы поедете в лагерь». На вопрос «Какие планы на лето?» в школе дети ответили: Петя: «Если мы поедем в лагерь, то родители поедут в дом отдыха». Галя: «Если мама с папой не поедут в дом отдыха, то мы не съездим в лагерь». Коля: «Если мы не поедем в лагерь, то и родители не поедут в дом отдыха». Чей ответ равносилен тому, что сказали родители?
10. Запишите предложения в виде предикатов с кванторами и постройте их отрицания:
а) Некоторые реки впадают в море;
б) Все люди знают, что земля круглая;
в) По крайней мере одно целое число делится на 8;
г) Не все птицы умеют летать;
д) Ни одна собака не умеет мяукать;
е) Хотя бы один студент хочет хорошо учиться;
ж) Никто из студентов не хочет быть отчисленным;
з) Все люди – братья.
и) Кто хочет, тот добьется.
11. На острове Фи живут рыцари, которые всегда говорят правду и лжецы, которые всегда лгут. Иногда там появляются обычные люди, которые могут и солгать, и сказать правду. Вам встретился человек и сказал: «Я лжец». Кто он? Житель острова или нет?
12. Островитянин Фей говорит в присутствии другого островитянина Фая: «По крайней мере один из нас Лжец!» Кто такой Фей и кто Фай?
13. Про трех человек Ай, Би и Си известно, что один из них рыцарь, другой – лжец, а третий приезжий, который может и правду сказать и солгать. Ай говорит: «Я приезжий». Би говорит: «Ай и Си иногда говорят правду». Си говорит: «Би приезжий». Кто из них кто?
14. Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытно, что один из нас русый, другой – брюнет, а третий – рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос имеет каждый из беседующих?
ТЕОРИЯ МНОЖЕСТВ
«Каждый сам знает, что он
понимает под множеством»
Е.Борель
Основные понятия
Математика утверждает, что теория множества появилась на свет 7.12.1873 г. В этот день Г. Кантор (1845 – 1918 профессор математики и философии в Галле) написал письмо Дедекинду (1831 – 1918 немецкий математик), в котором утверждал, что ему удалось посредством множеств доказать, что действительных чисел больше, чем натуральных.
Множество – основное математическое понятие. Его смысл выражается словами совокупность, набор и т. д. однотипных элементов, воспринимаемых как единое целое.
Множества обозначают большими латинскими буквами. Например, А = {Коля, Петя, Маша, Ира}, В = {1, 2, 7}, С = {1, 2, 3, 4, …, n, …}.
Все предметы, составляющие множества, называются элементами множества. Элементы множества обозначают маленькими латинскими буквами. Например, если элемент х принадлежит множеству К, то пишут х 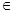 К, если элемент х не принадлежит множеству К, то пишут х
К, если элемент х не принадлежит множеству К, то пишут х 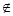 К.
К.
Есть множество, в котором нет ни одного элемента. Его называют пустым множеством и обозначают Ø.
Множество может быть конечным, если оно состоит из конечного числа элементов, и бесконечным, если оно содержит бесконечно много элементов. Примером конечного множества может служить множество дней недели, примером бесконечного множества – множество натуральных чисел.
Из школьного курса вам известны примеры бесконечных числовых множеств – множеств натуральных, целых, рациональных и действительных чисел.
Множество может быть задано:
· перечислением. Например, К = {2, 4, 20, 40};
· характеристическим свойством, т.е. свойством, характерным только для элементов этого множества. Например, 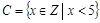 .
.
Из элементов множества А = {Коля, Петя, Маша, Ира}, например, можно составить новое множество М = {Петя, Маша}. Оно характеризуется тем, что все элементы М принадлежат множеству А. Говорят, что М – подмножество множества А и пишут М 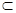 А.
А.
Множество М является подмножеством множества А, если всякий элемент множества М является элементом множества А и обозначают М 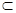 А.
А.
Например, множество всех первокурсников является подмножеством множества всех студентов.
Для любого множества А справедливо:
1) Само множество является своим подмножеством, т.е. А 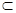 А.
А.
2) Пустое множество является подмножеством любого множества, т.е. Ø 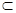 А.
А.
Пример:
Сколько можно составить подмножеств множества В?
1. В = {0, 1}, тогда {0} 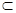 В, {1}
В, {1} 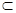 В, Ø
В, Ø 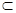 В, {0, 1}
В, {0, 1} 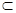 В – четыре.
В – четыре.
2. В = {1, 2, 3}, тогда {1} 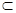 В, {2}
В, {2} 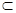 В, {3}
В, {3} 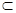 В, {1, 2}
В, {1, 2} 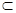 В, {1, 3}
В, {1, 3} 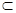 В, {2, 3}
В, {2, 3} 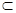 В, Ø
В, Ø 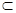 В, {1, 2, 3}
В, {1, 2, 3} 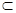 В – восемь.
В – восемь.
Можно доказать, что если в множестве n элементов, то оно имеет 2 n подмножеств.
Множества считаются равными, если они состоят из одних и тех же элементов. А также множества А и В равны, если А 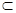 В и В
В и В 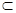 А.
А.
Пусть А= {2, 1, 3}, a В = {1, 2, 3} тогда А= В.
Операции над множествами
Над множествами производятся операции: пересечение, объединение, разность, дополнение.
Пересечением множеств А и В называется новое множество 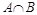 , которое состоит из всех элементов, принадлежащих одновременно множествам А и В, т.е.
, которое состоит из всех элементов, принадлежащих одновременно множествам А и В, т.е.  .
.
Объединением множеств А и В называется новое множество 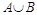 , которое состоит из всех элементов, принадлежащих хотя бы одному из множеств А или В, т.е.
, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств А или В, т.е. 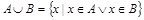 .
.
Разностью множеств А и В называется новое множество 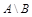 , которое состоит из всех элементов множества А, не принадлежащих множеству В, т.е.
, которое состоит из всех элементов множества А, не принадлежащих множеству В, т.е.  .
.
Дополнением множества А до множества В называется новое множество 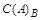 , которое состоит из всех элементов из
, которое состоит из всех элементов из 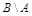 , т.е.
, т.е. 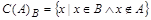 .
.
Выполнение операций с множествами удобно иллюстрировать на кругах Эйлера.
 | |||||||
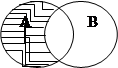 | |||||||
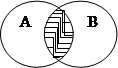 |  | ||||||
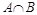
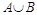
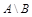
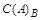
Пример:
Пусть Х = { a, б }, а Y = { a, в, с }, тогда 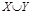 = { a, б, в, с },
= { a, б, в, с }, 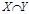 = { a },
= { a }, 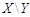 = { б },
= { б },  ,
, 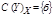 .
.
С помощью кругов Эйлера можно доказать следующие свойства множеств, справедливые для произвольных множеств А, В, С и D:
1) 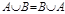 (коммутативность объединения);
(коммутативность объединения);
2) 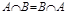 (коммутативность пересечения);
(коммутативность пересечения);
3)  (ассоциативность объединения);
(ассоциативность объединения);
4) 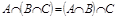 (ассоциативность пересечения);
(ассоциативность пересечения);
5)  (дистрибутивность объединения);
(дистрибутивность объединения);
6)  (дистрибутивность пересечения);
(дистрибутивность пересечения);
7) 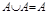 ;
;
8) 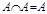 ;
;
9) 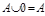 ;
;
10) 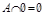 ;
;
11) 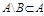 ;
;
12) 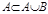 и
и  ;
;
13) 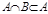 и
и 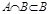 .
.
Пример:
В бригаде 25 человек. Среди них 20 моложе 30 лет, 15 старше 20 лет. Может ли так быть?
Решение: Может! Пусть А –множество членов бригады моложе 30 лет. В –множество членов бригады старше 20 лет. С –множество всех членов бригады. С = А 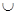 В. Так как 20+15 >25, то А
В. Так как 20+15 >25, то А 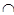 В ≠ Ø.
В ≠ Ø.
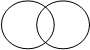 Из рисунка видно, что А
Из рисунка видно, что А 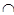 В составляет
В составляет
15 10 20 (15+20) – 25 =10 человек.
Тогда А состоит из 15 – 10 =5 членов,
В состоит из 20 – 10 = 10 членов.
Декартовым произведением множеств А и В называется новое множество 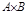 , элементами которого являются всевозможные пары
, элементами которого являются всевозможные пары  , где
, где  и
и 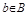 , т.е.
, т.е. 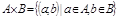 .
.
Упражнения
1. Изобразите с помощью кругов Эйлера множества: А – множество всех женщин, В – множество всех пенсионеров, С – множество людей, D – множество студенток АлтГПА, E – множество кошек, F – множество бездомных кошек. Выделите штриховкой женщин, не являющихся пенсионерами.
2. Изобразите с помощью кругов Эйлера следующие числовые множества: N – множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество действительных чисел.
3. Выберите верные утверждения: а) 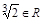 ; б)
; б) 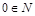 ; в)
; в) 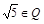 ; г)
; г)  ; д)
; д)  ; е)
; е) 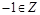 ; ж)
; ж) 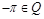 ; з)
; з) 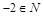 .
.
4. С помощью кругов Эйлера докажите равенства:
а) 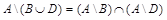 ; б)
; б) 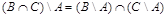 ;
;
в) 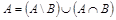 ; г)
; г) 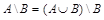 ;
;
д) 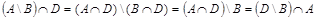 .
.
5. Расположите множества в порядке их включаемости друг в друга:
а) 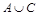 ,
, 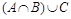 ,
, 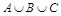 ,
, 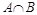 ;
;
б) 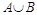 ,
, 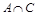 , А,
, А, 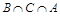 ,
, 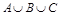 ;
;
в)  ,
, 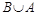 ,
, 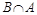 ,
, 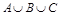 ;
;  ;
;
г)  , С,
, С, 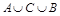 ,
, 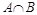 ,
, 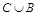 .
.
6. Найдите 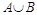 ;
; 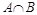 ;
;  ;
;  ;
;  , если:
, если:
а)  ;
; 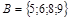 ; б)
; б)  ;
; 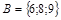 .
.
7. Найдите 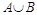 ;
; 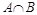 ;
;  ;
;  если:
если:
а) 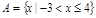 ,
,  ; б)
; б)  ,
,  .
.
8. Выпишите все подмножества множества 
9. Задайте множества перечислением:
а)  ; б)
; б) 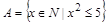 ;
;
в)  г)
г) 
10. В деревне 44 дома. В каждом доме живет одна семья. 25 семей держат коров, 28 – овец, 26 свиней, 15 – коров и овец, 13 – овец и свиней, 5 - коров, овец и свиней. Сколько семей держат коров и свиней?
11. В одной семье было много детей. 7 из них любили капусту, 6 – морковь, 5 – горох, 4 – капусту и морковь, 3 – капусту и горох, 2 – морковь и горох, один – и капусту, и морковь, и горох. Сколько детей было в семье?
12. Староста курса представил отчет преподавателю физкультуры: Всего студентов 45. Из них в футбольной секции – 25, баскетбольной – 30, шахматной – 28, футбольной и баскетбольной – 16, футбольной и шахматной – 18, баскетбольной и шахматной – 17, во всех трех секциях – 15. Отчет был забракован. Почему?
13. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком?
14. В сентябре было 12 дождливых дней, 8 ветреных, 4 холодных, 5 дождливых и ветреных, 3 дождливых и холодных, 2 ветреных и холодных, 1 дождливый, ветреный и холодный. Сколько было ясных дней?
3.КОМБИНАТОРИКА






