Числовые характеристики случайной величины

Рассмотри числовые характеристики только дискретной случайной величины. С числовыми характеристиками непрерывных случайных величин вы познакомитесь в курсе «Теории вероятностей и математической статистики».

1. Среднее арифметическое. Средним арифметическим значением случайной величины Х называется сумма произведений всех значений x_i этой величины на соответствующие им частости, обозначается 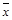и вычисляется по формуле: 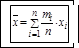, где n – общее значение случайной величины, m _i – частоты значения х _i.

2. Математическое ожидание. Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех её значений на соответствующие вероятности р_i:

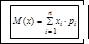, где р_i - вероятности значений случайной величины.

Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.

Математическое ожидание, как и среднее арифметическое, характеризует средний уровень значений случайной величины. При решении практических задач часто вместо математического ожидания выступает среднее арифметическое.

Пример:

Определить математическое ожидание числа очков, выпадающих при бросании игральной кости.

Решение: При бросании игральной кости случайная величина Х может принимать значения: 1, 2, 3, 4, 5, 6. Вероятность каждого из этих значений равна . Таким образом, закон распределения случайной величины запишем в таблицу:

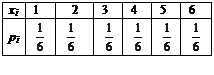
М (х) = 1· +2· +3· +4· +5· +6· = .

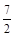Математическое ожидание частоты и частости события в серии независимых испытаний:

М (m) = np – математическое ожидание частоты события;

М (m/n) = p – математическое ожидание частоcти события равна вероятности осуществления этого события при единичном испытании, где

n – число испытаний, m – частота наступления события А есть случайная величина, m/n – частость, также случайная величина, p – вероятность события А при единичном испытании.

Пример: Даны две случайные величины их распределением:

xi	-8				уi	-4/3
рi	0,5	0,5			рi	0,3	0,7

Найдём их математические ожидания:

М (х) = -8·0,5+10· 0,5 = 1; М (у) = - 4/3·0,3 + 2· 0,7= 1.

Поясним геометрически:

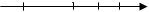- 8 0 1 10 х - 4/3 0 1 2 у

(первое распределение) (второе распределение)

Как видно случайные величины, имеющие одно и тоже математическое ожидание, могут вести себя по разному. У одной из них значения оказались более рассеянными по отношению к математическому ожиданию, у второй из них рассеивание значительно меньше. Отсюда следует, что необходимо иметь числовую характеристику, которая служила бы мерой рассеивания, разброса значений случайной величины. Такой числовой характеристикой является дисперсия.

3. Дисперсия. Степень отклонения (разброса) случайной величины от ее математического ожидания (от ожидаемого среднего значения) называется дисперсией и обозначается D (x) или D_x.

Для дискретных случайных величин используются формулы:

1) 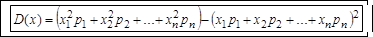или D (x) = М (х ²) – (М (х))² , дисперсия случайной величины равна математическому ожиданию квадрата случайной величины минус квадрат её математического ожидания.

2) 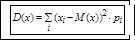- дисперсия случайной величины равна сумме квадратов отклонений отдельных значений случайной величины от её математического ожидания, умноженных на вероятность этих значений.

Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.

Пример: Случайная величина Х подчинена закону распределения

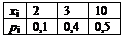Найти дисперсию.

Решение: Будем находить дисперсию по формуле D (x) = М (х ²) – (М (х))².

Сначала найдём математическое ожидание.

М (х)) = 2·0,1+ 3·0,4 + 10·0,5 = 6,4.

Далее найдём математическое ожидание квадрата случайной величины. М (х ²) = 2²·0,1+ 3²·0,4 + 10²·0,5 = 54;

D (x) = М (х ²) – (М (х))² = 54-6,4² = 13,04.

Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.

4. Среднее квадратическое отклонение (стандартное отклонение). Корень квадратный из дисперсии называется средним квадратическим отклонением или стандартным отклонением и обозначается σ (х).

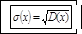
Дисперсия и стандартное отклонение характеризуют изменчивость (вариативность) случайной величины. Чем сильнее случайная величина отклоняется от своего математического ожидания, тем больше величины D (x) и σ (х).

Пример: Ряд распределения случайной величины Х имеет вид:

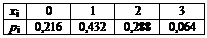Найти дисперсию и стандартное отклонение.

 

Решение: М (х) = 0·0,216+1·0,432+2·0,288+3·0,064=1,2;

М (х ²) = 0·0,216 +1²·0,432 + 2²·0,288 + 3²·0,064 = 2,16;

D (x) = М (х ²) – (М (х))² = 2,16 – 1,2² = 0,72;

σ (х) = 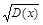= = 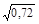0,84.

 

Упражнения

1. В коробке 7 карандашей, из которых 4 карандаша красные. Наугад взяли 4 карандаша. Найти закон распределения числа вынутых красных карандашей, математическое ожидание, дисперсию и среднее квадратическое отклонение.

2. По одному и тому же маршруту в один и тот же день совершают полет 3 самолета. Каждый из них с вероятностью 0,7 может произвести посадку по расписанию. Составить таблицу распределения числа самолетов, отклонившихся от расписания, найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

3. Производится n независимых выстрелов с вероятностью попадания р при каждом выстреле. Найти распределение числа попаданий в мишень. Составить функцию распределения и построить её график. Найти математическое ожидание, дисперсию и стандартное отклонение.

1) n = 4, p = 0,6; 2) n = 4, p = 0,5; 3) n = 3, p = 0,6;

4) n = 4, p = 0,7; 5) n =5, p = 0,8; 6) n = 3, p = 0,5.

4. Набрасываются кольца на колышек либо до первого попадания, либо до полного израсходования всех колец, число которых равно n. Составить таблицы распределения вероятностей случайного числа брошенных колец, если вероятность набрасывания кольца на колышек при каждом испытании постоянна и равна p.

1) n = 5, p = 0,8; 2) n = 4, p = 0,8; 3) n = 3, p = 0,6;

4) n = 6, p = 0,9; 5) n = 3, p = 0,8; 6) n = 7, p = 0,5.

5.Участник игры в лапту k раз бьёт по мячу. Вероятность попадания в мяч лаптой при каждом ударе одинакова и равна p. Составить таблицы распределения вероятностей случайного числа попадания в мяч.

1) n = 4, p = 0,3; 2) n = 4, p = 0,2; 3) n = 3, p = 0,4;

4) n = 6, p = 0,4; 5) n = 3, p = 0,1; 6) n = 7, p = 0,3.

6. У охотника 4 патрона. Он стреляет по зайцу пока не попадет или пока не кончатся патроны. Составить таблицу распределения числа израсходованных патронов. Вероятность его попадания при одном выстреле равна 0,6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.