Как правило, необработанные экспериментальные данные представлены в виде неупорядоченного набора чисел. Необходима обработка.
1. Группировка. Группировка представляет собой процесс систематизации и выполняется различными методами. Основная цель группировки - представление данных в компактной форме, наглядной и удобной для анализа. Рассмотрим группировку на конкретном примере.
В таблице 1приведены данные (бег 5 км, лыжи, девушки 1-го курса ФФК).
Таблица 1
| 25,7 27,0 28,1 27,1 26,4 | 28,2 26,7 29,5 27,3 28,4 | 27,2 30,0 27,1 28,2 27,4 | 25,5 29,6 26,7 25,3 26,4. | 27,2 27,8 29,4 27,5 29,2 | 27,3 28,4 26,1 29,3 27,4 | 26,4 29,3 27,2 29,1 30,5 | 27,1 27,5 25,6 28,1 28,3 | 28,3 27,3 28,1 27,1 27,0 | 27,4 27,0 27,5 26,0 27,1 |
Объем выборки в данном случае равен 50 т. е. n = 50.
Группировка заключается в распределении вариант выборки по группам или интервалам группировки. Каждый интервал содержит определенное количество значений изучаемого признака. Число интервалов группировки ищется либо по Формуле Стерджеса: к =1+3.33*lg(n), либо с помощью таблицы 2. Ширина каждого интервала определяется по формуле: 
где h - ширина интервала, x max, x min - максимальная и минимальная варианты выборки.
Таблица 2
Для нашего примера при n = 50 число интервалов группировки к = 7.
. Округлим ширину интервала h в сторону увеличения и примем h = 0,8.
Найдём границы интервалов группировки по формулам:
х н1 = x min -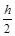 
; х н2 = x н1+h; х н2 = х в1 ; х н3 = х в2 и т.д., где
х н1- нижняя граница первого интервала.
х н2- нижняя граница второго интервала.
х в1- верхняя граница первого интервала и т. д.
Найдём нижние и верхние границы интервалов, причем верхнюю границу первого интервала будем записывать на 0,1 меньше нижней границы второго интервала и т.п.
х н1= 25,3 -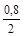 
= 24,9; х н2 = 24,9 + 0,8 = 25,7, тогда х в1 = 25,8.
После того как найдены границы всех интервалов, распределим по этим интервалам выборочные варианты, но для удобства последующей обработки вычислим срединные значения интервалов группировки х сi по формуле х сi= х нi+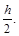 
Результаты внесем в таблицу 3.
Но прежде рассмотрим ряд определений.
Накопленная частота интервала – это число, полученное последовательным суммированием частот в направлении от 1 интервала и до того интервала включительно,для которого определяется накопленная частота.
Частостью называется отношение частоты к объему выборки и обозначается f i, т.е. f i =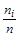 
. Сумма всех частостей всегда ровна 1
Накопленной частостью называется отношение накопленной частоты к объему выборки и обозначается F i, т.е. F i =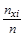 
.
Таблица 3
1 столбец: номера интервалов;
2 столбец: границы интервалов;
3 столбец: срединные значения интервалов группировки;
4 столбец: повторяемость вариант в каждом интервале;
5 столбец: частота – это количество, встречающихся в выборке вариантов. Общая сумма всех частот равна объёму выборки, т.е. n = 
.
6 столбец: накопленная частота;
7 столбeц: частность;
8 столбец: накопленная частность.
