Математическая логика – это раздел математики, основной вопрос которой «Как определить справедливость суждения?».
Одни повествовательные предложения выражают истину, другие – ложь, а третьи – ни то, ни другое. Те предложения, которые выражают истину или ложь, называют высказываниями.
Высказывание – это повествовательное предложение, о котором можно однозначно сказать – истинно оно или ложно.
Например: а) «8 – нечетное число», «Барнаул – столица России», «В АлтГПА нет столовой» - это высказывания, при чем ложные;
б) « », «А.С. Пушкин – автор произведения «Евгений Онегин»», «АлтГПА основана в 1933 г.» - это высказывания, при чем истинные;
», «А.С. Пушкин – автор произведения «Евгений Онегин»», «АлтГПА основана в 1933 г.» - это высказывания, при чем истинные;
в) «АлтГПА – самый лучший вуз в России», «Сегодня на улице тепло», «Математика интереснее психологии», «Охранник работает хорошо» - не являются высказываниями, т.к. однозначно нельзя определить их истинность;
г) «Который сейчас час?», «Будь здоров!», «Стой!», «Кто идет?», «С днем рождения!», «Как дела?» - это не высказывания, т.к. не являются повествовательными предложениями.
Высказывания обозначают большими латинскими буквами.
Запись  означает «Высказывание А истинно», а запись
означает «Высказывание А истинно», а запись  - «Высказывание А - ложно».
- «Высказывание А - ложно».
Из одних высказываний можно получить другие с помощью частицы «не», союзов «и» и «или», слов «если, то», «тогда и только тогда, когда» и «неверно, что». Таким образом, над высказываниями выполняют следующие операции: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Отрицанием высказывания А называется новое высказывание  (читают «не А» или «неверно, что А»), которое истинно, когда А ложно и ложно, когда А истинно.
(читают «не А» или «неверно, что А»), которое истинно, когда А ложно и ложно, когда А истинно.
Конъюнкцией высказываний А и В называется новое высказывание  (читают «А и В»), которое истинно только в том случае, когда оба высказывания А и В истинны; в остальных случаях – ложно.
(читают «А и В»), которое истинно только в том случае, когда оба высказывания А и В истинны; в остальных случаях – ложно.
Дизъюнкцией высказываний А и В называется новое высказывание 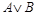 (читают «А или В»), которое истинно в том случае, если хотя бы одно из высказываний А или В истинно; и ложно, если оба высказывания А и В ложны.
(читают «А или В»), которое истинно в том случае, если хотя бы одно из высказываний А или В истинно; и ложно, если оба высказывания А и В ложны.
Импликацией высказываний А и В называется новое высказывание  (читают «если А, то В» или «из А следует В»), которое ложно только в том случае, когда высказывание А истинно, а В - ложно; в остальных случаях истинно.
(читают «если А, то В» или «из А следует В»), которое ложно только в том случае, когда высказывание А истинно, а В - ложно; в остальных случаях истинно.
В таком случае высказывание А называют посылкой или условием, а В – заключением или следствием.
Эквиваленцией высказываний А и В называется новое высказывание 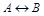 (читают «А тогда и только тогда, когда В»), которое истинно в том случае, когда высказывания А и В принимают значения одинаковой истинности (оба истинны или оба ложны); в остальных случаях – ложно.
(читают «А тогда и только тогда, когда В»), которое истинно в том случае, когда высказывания А и В принимают значения одинаковой истинности (оба истинны или оба ложны); в остальных случаях – ложно.
С помощью введенных операций можно строить сложные высказывания. Значения истинности сложных высказываний удобно представлять в виде таблиц истинности. При этом, если таблица истинности строится для n высказываний (которые всегда занимают первые столбцы), то в ней будет 2n строк (кроме строки заголовка).
| А | В | 
| 
| 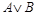
| 
| 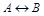
|
Например: Истинно или ложно предложение:
а) «Геометрия – часть математики или ботаники».
Решение: Пусть высказывание А: «Геометрия – часть математики», В: «Геометрия – часть ботаники». Тогда имеем дизъюнкцию 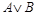 , которая является истинной в силу того, что
, которая является истинной в силу того, что  , а
, а  . Значит данное предложение – истина.
. Значит данное предложение – истина.
б) «Если Париж – столица Англии, то карась – не рыба».
Решение: Пусть высказывание А: «Париж – столица Англии», В: «Карась – не рыба». Тогда имеем импликацию  , которая является истинной в силу того, что
, которая является истинной в силу того, что  и
и  . Значит данное предложение – истина.
. Значит данное предложение – истина.
в) «2*2=5 тогда и только тогда, когда 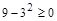 ».
».
Решение: Пусть высказывание А: «2*2=5», В: «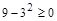 ». Тогда имеем эквиваленцию
». Тогда имеем эквиваленцию 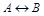 , которая является ложной в силу того, что
, которая является ложной в силу того, что  , а
, а 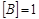 . Значит данное предложение – ложь.
. Значит данное предложение – ложь.






