а у²+ b у¢+ c у=R(x), где а, b, c – некоторые постоянные.
Его общее решение имеет вид:  , где
, где
 - общее решение ЛОДУ II а у²+ b у¢+ c у=0;
- общее решение ЛОДУ II а у²+ b у¢+ c у=0;
 - частное решение ЛНДУ II а у²+ b у¢+ c у=R(x), которое ищется, в зависимости от правой части по одному из правил.
- частное решение ЛНДУ II а у²+ b у¢+ c у=R(x), которое ищется, в зависимости от правой части по одному из правил.
Правило 1: если правая часть R(x)=Р(х)еkx, где Р(х) – какой-либо многочлен степени m, и если:
· k – не является корнем характеристического уравнения а k2+ b k+ c =0, то у*=Q(х)еkx, где Q(х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.
· k – является однократным корнем характеристического уравнения (то есть один из неравных корней D>0) а k2+ b k+ c =0, то у*=хQ(х)еkx, где Q(х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.
· k – является двукратным корнем характеристического уравнения (то есть один из равных корней D=0) а k2+ b k+ c =0, то у*=х2Q(х)еkx, где Q(х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.
Замечание 1: Если множитель Р(х) – есть постоянная величина (многочлен нулевой степени), то Q(x) – тоже постоянная величина (многочлен нулевой степени).
Замечание 2: Если множитель R(х) –многочлен, то есть k=0, то y* тоже многочлен.
Правило 2: если правая часть R(x)=еax(P1(x)cosbx+P2(x)sinbx) где P1(x) и P2(x) –многочлены соответственно степеней m1 и m2, и если:
· комплексные числа a±bi – не является корнями характеристического уравнения а k2+ b k+ c =0, то у*=еax(Q1(x)cosbx+Q2(x)sinbx), где Q1(x) и Q2(x) –многочлены, степени которых не превышают старшей из степеней m1 и m2.
· комплексные числа a±bi – является корнями характеристического уравнения а k2+ b k+ c =0, то у*=хеax(Q1(x)cosbx+Q2(x)sinbx), где Q1(x) и Q2(x) –многочлены, степени которых не превышают старшей из степеней m1 и m2.
.
| Греческий алфавит | ||||
| Aa | альфа | Nn | ню (ни) | |
| Bb | бэта (бета) | Xx | кси | |
| Gg | гамма | Oo | омикрон | |
| Dd | дельта | Pp | пи | |
| Ee | эпсилон (ипсилон) | Rr | ро | |
| Zz | дзета | Ss | сигма | |
| Hh | эта | Tt | тау | |
| QqJ | тэта | Ffj | фи | |
| Ii | йота | Cc | хи | |
| Kk | каппа | Uu | юпсилон (ипсилон) | |
| Ll | ламбда (лямбда) | Yy | пси | |
| Mm | мю (ми) | Ww | омега |
Опр: Пусть дана числовая последовательность а1, а 2, а 3,..., аn,... Выражение вида

называется числовым рядом или просто рядом. Числа а 1, а 2, а 3,..., а n... называются членами ряда, член аn с произвольным номером — общим членом ряда. Суммы конечного числа членов ряда S 1= а 1, S 2= а 1+ а 2, S 3= а 1+ а 2+ а 3,…, S n= а 1+ а 2+ а 3+…+ аn,
называются частичными суммами ряда.
Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм S 1, S 2, S 3,..., S n,...
Опр: Ряд называется сходящимся, если последовательность его частичных сумм сходится к какому-нибудь числу S, которое в этом случае называется суммой ряда. Это записывается так:

Опр: Ряд называется расходящимся, если последовательность его частичных сумм расходится.
Геометрическая прогрессия: bn = b 1· qn -1;  ;
;
Частичная сумма Sn, при q¹1 имеет вид:

Если |q|<1, то 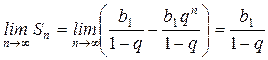 , то ряд сходится; , то ряд сходится;
|
Если |q|³1, то  , то ряд расходится. , то ряд расходится.
|






