Если 
и 
- дифференцируемые функции своих аргументов, то производная сложной функции 
существует и равна произведению производной данной функции y по промежуточному аргументу z на производную промежуточного аргумента z по независимой переменной x:
.
Пример 1. Найти производную функции 
.
Решение. 
.
Пример 2. Найти производную функции 
.
Решение. 
.
Пример 3. Найти производную функции 
.
Решение.
Понятие производной находит многочисленные приложения. С помощью производной можно найти касательную к кривой в данной точке, определить скорость и ускорение неравномерного движения в данный момент времени. Производная широко применяется при исследовании функций.
Исследование функции можно проводить по следующей схеме:
1. Найти область существования функции.
2. Исследовать функцию на четность нечетность, определить симметрию графика.
3. Исследовать поведение функции в граничных точках области определения.
4. Найти промежутки возрастания и убывания функции, точки экстремума.
5. Вычислить значения экстремума.
6. Определить интервалы выпуклости и вогнутости графика, найти точки перегиба.
7. Найти точки пересечения графика функции с координатными осями.
8. Найти асимптоты графика функции.
Если исследуемая функция четная или нечетная, достаточно исследовать функцию и построить её график для положительных значений аргумента из области определения.
Иногда порядок исследования целесообразно выбирать, исходя из конкретных особенностей данной функции.
Дифференциалом функции y=f(x) называется произведение ее производной на дифференциал независимой переменной dy=f¢(x)dx. Дифференциал функции является главной частью ее приращения, линейной относительно приращения независимой переменной: dy=Dy+e, dy» Dy. Эта формула используется в приближенных вычислениях с помощью дифференциала: f(x0+Dx)» f(x0)+f¢(x0)Dx.
Пример 4. Построить график функции 
.
Решение. Функция определена и непрерывна при всех х. Первая производная
существует всюду, за исключением точек х1 =0, х2 =6.
Исследуем предельные значения производной при х, стремящемся к нулю слева и справа:
; 
,
при х < 0 у' <0, при х > 0 у' > 0, следовательно функция имеет минимум в точке х = 0, причем уmin = 0.
Рассмотрим критическую точку х2 = 6. При х → 6 – 0 у' → – ∞, при х → 6 + 0 также
у' → – ∞, т.е. производная отрицательна слева и справа от точки х2 = 6, поэтому в данной точке экстремума нет. В этой точке функция убывает, касательная к кривой в точке х2 = 6 вертикальна.
При х = 4 производная обращается в нуль. Так как при х < 4 у' > 0, при х > 4 у' < 0, то х = 4 – точка максимума, причём уmax = 
.
Таким образом, в промежутке (– ∞, 0) функция убывает, в промежутке (0, 4) – возрастает,в промежутке (4, +∞) – убывает.
Определяем точки перегиба и интервалы выпуклости и вогнутости кривой. Вторая производная 
в нуль не обращается ни в одной точке,
в точках х = 0 и х = 6 она не определена.
Исследуем знак второй производной вблизи этих точек. Так как у''< 0 при х < 0 и при х >0, то кривая выпукла вверх слева и справа от точки с абсциссой х = 0 и, следовательно, точка О (0,0) не является точкой перегиба; с другой стороны, О – точка минимума (такая точка называется точкой возврата).
При х < 6 у'' <0,при х > 6 у'' > 0, поэтому точка (6, 0) является точкой перегиба.
Определим асимптоты кривой:
;
.
Следовательно, прямая у = – х +2 является асимптотой кривой .
Упражнения. 
2.5.1. Найти производные функций
a) y = 2x + 8, y = 3x2 + x + 7, y =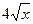 
+ x2 - 5,
y = x4+ 
, y = 2x4 + x2 + 
+ 9, y = 3 - 7x + 8x3.
b) y = (x-3)(x+5 ), y = x3(x - ), y = 3x(x2 - 
),
y = (x3 – 2x +1)(1-5x-8x2), y = (t3 – 3 
)(1- ).
c) y = 
, y = 
, y = 
,
y = 
, y = 
,
y = 
d) y = (21-15x2+x3)2, y = (x3-7)4, y = 
,
y = 
.
e) y = (x +4)ex, 
, 
, 
, 
.
f) 
, 
, 
, 
.
g) 
, 
, 
, 
.
h) 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
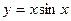i) 
, 
, 
, 
, 
, 
.
j) 
, 
, 
, 
.
k) y = 
, 
, 
, 
.
l) 
, 
, 
, 
.
m) 
; 
; 
; 
.
n) 
; 
; 
; 
.
о) 
.
2.2. Вычислить приближенно значение 
, заменив в точке х=х0 приращение функции 
дифференциалом:
а = 502; х0 = 512
а = 267; х0 = 256
а = 234; х0 = 243.
2.3. С помощью дифференциала вычислить приближенное значение:
a) ln1,2; b) сos 290; c) 
; d) sin 310; e) (1,12)3; f) 
;
g)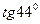 
; h) 
; I) 
.
2.4. Найти точки экстремума функций:
a) 
; b) 
; c) 
;
d) 
; e) 
; f) 
.
2.5. Найти точки перегиба функций 
2.6. Найти асимптоты кривых
а) 
b) 
c) 
d) 
e) 
2.7. Исследовать функции и построить график:
a) 
; b) 
;
c) 
; d) 
e) 
; f) 
;
g) 
; h) 
;
I) 
;
j) 
; k) 
;
l) 
; m) 
;
n) 
; o) 
;
p) 
; q) 
.
2.8 Найти наибольшее и наименьшее значение функции:
a) y = 3x2 – 6 на [0; 3]
b) y = 
на(1; е ]
c) y = 
на [0; 4]
d) y = 
на [-2; 2]
e) y = 
на [1; 3]
f) y = 
на [0; 
]
g) y = 
на [1; e ]
h) y = 
на [-2; 2]
