1. Предел числовой последовательности и предел функции.
2. Виды неопределенностей. Раскрытие неопределенностей.
3. Первый и второй замечательные пределы.
4. Производные и дифференциалы высших порядков. Экономический смысл производной.
5. Дифференцирование сложной функции, заданной неявно, логарифмическое дифференцирование.
6. Касательная и нормаль к плоской кривой.
7. Основные свойства дифференцируемых функций. Теоремы Ферма, Роля, Лагранжа.
8. Правило Лопиталя.
9. Признаки возрастания и убывания функции. Необходимое и достаточное условия существования экстремума.
10. 7.. Выпуклость, вогнутость, точки перегиба.
11. Асимптоты графика функции.
12. Дифференциал, его свойства и приложения.
13. Определение функции нескольких переменных. Непрерывность функции.
14. Частное и полное приращение функции нескольких переменных. Частные производные.
15. Полный дифференциал функции нескольких переменных, его использование в приближенных вычислениях.
16. Частные производные высших порядков.
17. Производная по направлению. Градиент.
18. Экстремум функции двух переменных. Необходимое и достаточное условия.
19. Понятие об эмпирических формулах и методе наименьших квадратов.
20.. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов.
21. Основные методы интегрирования: метод разложения, замены переменной и интегрирования по частям.
22. Интегрирование рациональных дробей.
23. Определенный интеграл как предел интегральной суммы.
24. Формула Ньютона-Лейбница.
25. Метод подстановки и интегрирование по частям в определенном интеграле.
26. Несобственные интегралы.
27. Вычисление площадей плоских фигур.
28. Вычисление объемов тел вращения.
29. Вычисление поверхности тела вращения
30. Определение комплексного числа. Способы задания.
31. Алгебраические операции над комплексными числами.
32. Числовые ряды. Сходимость ряда. Необходимый признак сходимости.
33. Достаточные признаки сходимости знакоположительных рядов: признак сравнения, Даламбера, радиакальный и интегральный признак Коши.
34. Знакочередующиеся ряды. Теорема Лейбница.
35. Абсолютная и условная сходимость ряда.
36. Степенные ряды. Радиус, интервал и область сходимости.
37. Ряды Тейлора и Маклорена. Разложение функции в степенной ряд.
38. Вычисление значений функций с помощью степенного ряда.
39. Вычисление определенных интегралов с помощью степенных рядов.
- Предмет и основные понятия теории вероятностей
- События и их классификация.
- Классическое определение вероятности.
- Элементы комбинаторики.
- Алгебра событий
- Теорема сложения совместных событий.
- Теорема сложения несовместных событий.
- Теорема умножения независимых событий.
- Теорема умножения зависимых событий.
- Формула полной вероятности.
- Формула проверки гипотез Байеса.
- Формула Бернулли.
- Формула Пуассона.
- Локальная теорема Муавра-Лапласа. Функция Гаусса и ее свойства.
- Интегральная теорема Муавра-Лапласа. Функция Лапласа и ее свойства.
- Следствия из интегральной теоремы Муавра-Лапласа.
- Определение и виды случайных величин.
- Закон распределения дискретной случайной величины.
- Биномиальный и пуассоновский законы распределения.
- Операции над случайными величинами.
- Характеристики дискретной случайной величины и их свойства.
- Функция распределения и ее свойства.
- Плотность вероятности и ее свойства.
- Определение непрерывных случайных величин. Примеры.
- Характеристики непрерывных случайных величин и их свойства.
- Равномерный закон распределения. Характеристики.
- Показательный закон распределения. Характеристики.
- Нормальный закон распределения. Характеристики.
- Правило трех сигм.
- Принцип практической уверенности. Уровень значимости.
- Лемма Чебышева.
- Неравенство Чебышева. Частные случаи.
- Теорема Чебышева и ее следствия.
- Понятие о центральной предельной теореме Ляпунова.
- Генеральная и выборочная совокупности. Методы и цели образования выборок.
- Ошибки выборочных наблюдений.
- Вариационный ряд. Графическое представление.
- Характеристики вариационного ряда и их свойства.
- Доверительная вероятность и доверительный интервал.
- Необходимый объем выборок.
- Статистические гипотезы и статистические критерии.
- Проверка статистических гипотез о равенстве средней, дисперсий.
- Проверка гипотезы о законе распределения. Критерии Пирсона, Колмогорова.
- Функциональная, статистическая и корреляционная зависимости.
- Корреляционная таблица и ее характеристики.
- Основные задачи корреляционно-регрессионного анализа.
- Прямая регрессия.
87. Коэффициенты регрессии и их свойства. Коэффициент корреляции и его свойства.
4.4.Перечень вопросов, заданий, тестов для зачета/ экзамена:
Типовые варианты контрольных работ
Контрольная работа № 1
1. Найти предел: 
.
2. Найти производную функции: 
.
3. Найти уравнение касательной к кривой 
, которая перпендикулярна прямой 3y-x+3=0. Сделать чертеж.
4. Исследовать функцию y=x2(x-1)2 и схематично построить ее график.
Контрольная работа № 2
1. Найти неопределенный интеграл:
2. Вычислить определенный интеграл:
3. Найти площадь фигуры, ограниченной линиями: 
, 
, 
. Сделать чертеж.
4. Исследовать сходимость ряда: 
Типовые контрольные тесты
Контрольный тест по теме «Дифференциальное исчисление»
1. Функция 
на интервале (-2;0)
а) монотонно возрастает;
в) имеет минимум;
с) имеет максимум;
д) монотонно убывает.
2. Если каждому значению 
ставится в соответствие по определенному закону некоторое число 
, то множество занумерованных чисел х1, х2, …,хn называется
а) функционалом;
в) числовым рядом;
с) рядом чисел;
д) числовой последовательностью.
3. Область определения функции 
есть
а) (-1;∞) в) (0;∞) с) (-∞;2) 
(2; ∞) д)(- ∞;∞).
4. 
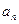- бесконечно малая последовательность. Тогда
а) 
в) 
с) предел не существует
д) 
5. Производная 
функции 
в точке Р0(1;1) в направлении, задаваемом вектором 
равна
а) 
в) 
с) 
д) 
.
6. Если х и у – две переменные величины, причем 
то 
есть
а) 
, если 
в) не определен
с)
д) не связан с а и b
7. Горизонтальная асимптота кривой 
есть
а) 
в) 
с) д) 
8. Уравнение нормали к кривой 
а) 
в) 
с) 
д) 
.
9. Вертикальная асимптота кривой 
будет
а) 
в) 
с) 
д) 
10. 
а) равен 0 в) не существует с) равен 3 д) равен 3/2
11. Область значений функции 
есть
а) 
в) [0;1)
с) 
д) [0;1]
12. Неявная функция задана уравнением 
. Тогда производная 
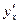равна
а) 
в) 
с) 
д) 
13. Полным дифференциалом функции 
называется выражение
а) 
в) 
с) 
д) 
14. Точкой перегиба функции 
является точка, при переходе через которую
а) 
сохраняет знак
в) меняет знак
с) 
меняет знак
д) сохраняет знак
15. Точка М(1;1) для функции 
является точкой
а) разрыва
в) минимума
с) перегиба
д) максимума
Типовой тест по математике (начальный уровень)
1. Функция 
является
а) нечетной б) содержит нечетную степень
в) четной г) ни четной, ни нечетной
2. Область определения функции 
есть
а) 
б) 
в) 
г) 
3. График четной функции симметричен относительно
а) оси абсцисс б) начала координат
в) оси ординат г) биссектрисы I координатного угла
4. Для функции 
период равен
а) 4π б) 8π в) π г) π/2
5. Для функции 
обратной является функция
а) 
б) 
в) 
г) 
6. Производная функции 
равна
а) 
б) 
в) 
г) 
7. 
равен
а) 3 б) ∞ в) 0 г) 7
8. Закон движения материальной точки имеет вид 
, где 
- координаты точки в момент времени t. Тогда скорость точки при t = 2 равна
а) 8 б) 4 в) 2 г) 1
9. 
равен
а) 8 б) –8 в) 0 г) 16
10. 
равен
а) 
б) 
в) 
г) правильный ответ не указан
11. Функция 
является убывающей на интервале, если на этом интервале
а) 
б) 
в) 
г) 
12. Стационарными точками функции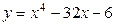 
являются точки
а) 
б) 
в) 
г) 
13. Множество первообразных функции 
имеет вид
а) 
б) 
в) 
г) 
14. Для дифференциального уравнения 
характеристическое уравнение имеет вид
а) 
б) 
в) 
г) 
