Пусть между переменными x и y предполагается функциональная зависимость y = f(x), подлежащая определению.
Имеется ряд наблюдений переменных x и y:
| xi | x1 | x2 | … | xn |
| yi | y1 | y2 | … | yn |
По этим данным можно построить ломаную, вид которой указывает вид эмпирической формулы. Если анализ опытных данных привел к выводу, что между переменными x и y существует линейная зависимость, 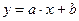 , то параметры
, то параметры  и
и 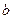 этой прямой определяются из системы уравнений:
этой прямой определяются из системы уравнений: 
Упражнения.
3.1.1.Опытные данные о значениях переменных x и y приведены в таблице:
| x | 0,6 | 1,0 | 1,4 | 1,8 | 2,2 |
| y | 7,8 | 10,5 | 12,7 | 14,3 | 15,5 |
В результате их выравнивания по параболе получено уравнение y = - 1,5x2 + 9x + 3. Пользуясь МНК аппроксимировать эти данные линейной зависимостью y = ax + b. Установить, какая из двух линий лучше выравнивает экспериментальные данные. Сделать чертёж.
3.1.2. Опытные данные о значениях переменных x и y приведены в таблице:
| x | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 |
| y | 1,95 | 1,9 | 1,8 | 1,7 | 1,65 |
В результате их выравнивания по гиперболе получено уравнение
y = (x + 1)/(x – 1). Пользуясь МНК аппроксимировать эти данные линейной зависимостью y = ax + b. Установить, какая из двух линий лучше выравнивает экспериментальные данные. Сделать чертёж.
3.1.3. Опытные данные о значениях переменных x и y приведены в таблице:
| x | |||||
| y | 1,6 | 2,0 | 2,3 | 2,4 | 2,7 |
В результате их выравнивания по параболе получено уравнение 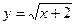 . Пользуясь МНК аппроксимировать эти данные линейной зависимостью y = ax + b. Установить, какая из двух линий лучше выравнивает экспериментальные данные. Сделать чертёж.
. Пользуясь МНК аппроксимировать эти данные линейной зависимостью y = ax + b. Установить, какая из двух линий лучше выравнивает экспериментальные данные. Сделать чертёж.
3.1.4. Опытные данные о значениях переменных x и y приведены в таблице:
| x | |||||
| y |
В результате их выравнивания получено уравнение y =  . Пользуясь МНК аппроксимировать эти данные линейной зависимостью y = ax + b. Установить, какая из двух линий лучше выравнивает экспериментальные данные. Сделать чертёж.
. Пользуясь МНК аппроксимировать эти данные линейной зависимостью y = ax + b. Установить, какая из двух линий лучше выравнивает экспериментальные данные. Сделать чертёж.
3.1.5. Опытные данные о значениях переменных x и y приведены в таблице:
| x | -2 | ||||
| y | 0,3 | 1,0 | 1,5 | 2,0 | 3,0 |
В результате их выравнивания по экспоненте получено уравнение y = еx/5. Пользуясь МНК аппроксимировать эти данные линейной зависимостью y = ax + b. Установить, какая из двух линий лучше выравнивает экспериментальные данные. Сделать чертёж.
Интегральное исчисление
Неопределенный интеграл
Первообразной функцией для функции f (x) называется такая функция F (x), производная которой равна данной функции, т.е. F' (x) = f (x).
Неопределенным интегралом от непрерывной функции f (x) или от дифференциального выражения f (x) dx называется совокупность первообразных функций f (x).
Обозначение:
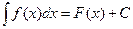 , где F' (x) = f (x). Функция f (x) называется подынтегральной функцией, а выражение f (x) dx – подынтегральным выражением.
, где F' (x) = f (x). Функция f (x) называется подынтегральной функцией, а выражение f (x) dx – подынтегральным выражением.
Свойства неопределенного интеграла:
Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
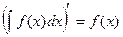 ; d
; d  ;
;
Неопределенный интеграл от дифференциала функции f (x) равен функции f (x) с точностью до постоянного слагаемого
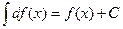 .
.
Постоянный множитель в подынтегральном выражении можно выносить за знак неопределенного интеграла
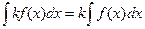 .
.
Неопределенный интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов этих функций
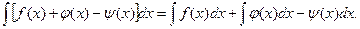
Таблица простейших неопределенных интегралов
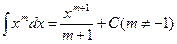 .
. 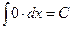 .
. 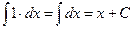 .
.
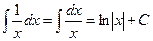 .
. 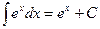 .
. 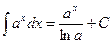 .
.
 .
.  .
. 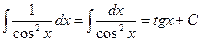 .
.
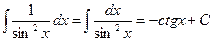 .
. 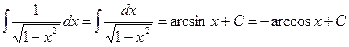 .
.
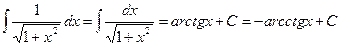 .
. 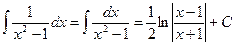 .
.
Методы интегрирования.
Интегрирование разложением.
Если 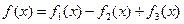 , то
, то 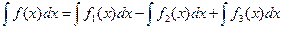 .
.
Пример 1. Найти интеграл  .
.
Решение.
 =
= 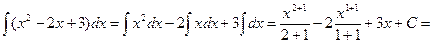
 .
.
Метод подстановки.
Интегрирование путем введения новой переменной (метод подстановки) основано на формуле 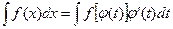 , где
, где 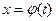 - дифференцируемая функция переменной t.
- дифференцируемая функция переменной t.
Пример 2. Найти интеграл 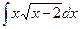 .
.
Решение. Положим 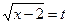 , тогда
, тогда  , откуда
, откуда 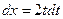 .
.
Подставляя полученные равенства в подынтегральное выражение, находим
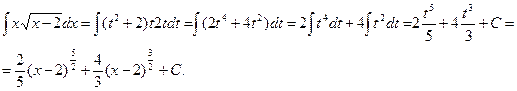
Метод интегрирования по частям.
Если 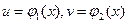 - дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций
- дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций 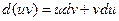 получается формула интегрирования по частям
получается формула интегрирования по частям  .
.
Пример 3. Найти 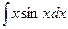 .
.
Решение. Обозначим: 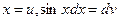 , отсюда dx = du, v = - cosx.
, отсюда dx = du, v = - cosx.
Подставляя значения u,v,du,dv в формулу интегрирования по частям, получим 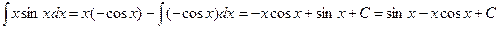 .
.
Упражнения.
4.1. Найти неопределенные интегралы:
a) 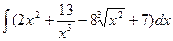 ; b)
; b) 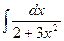 ;
;
c) 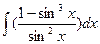 ; d)
; d) 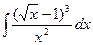 ;
;
e)  ; f)
; f) 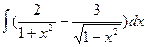 ;
;
g) 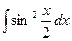 ; h)
; h) 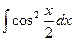 ;
;
i) 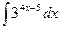 ; j)
; j) 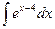 ;
;
k) 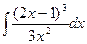 ; l)
; l) 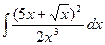 .
.
4.2. Найти неопределенные интегралы методом замены переменной:
a) 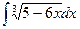 ; b)
; b) 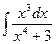 ; c)
; c) 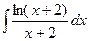 ; d)
; d) 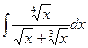 ;
;
e) 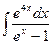 ; f)
; f)  ; g)
; g) 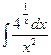 ; h)
; h) 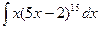 ;
;
i)  ; j)
; j) 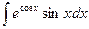 ; k)
; k) 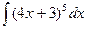 ; l)
; l) 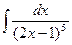 ; m)
; m) 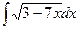
4.3. Найти неопределенные интегралы методом интегрирования по частям:
a) 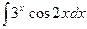 ; b)
; b) 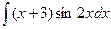 ; c)
; c) 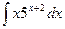 ; d)
; d) 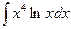 ;
;
e)  ; f)
; f) 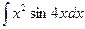 ; g)
; g) 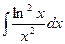 ; h)
; h) 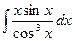 ;
;
h) 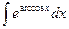 ; I)
; I)  .
.
4.4. Интегрирование рациональных дробей:
a) 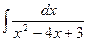 ; b)
; b) 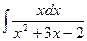 ; c)
; c) 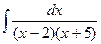 ;
;
d) 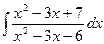 ; e)
; e) 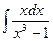 ; f)
; f) 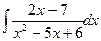 ; q)
; q) 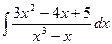 .
.
7.5. Интегрирование иррациональных выражений:
а) 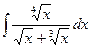 ; b)
; b)  ; с)
; с) 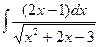 ; d)
; d) 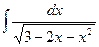 .
.




