ОБЕСПЕЧЕНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ (МОДУЛЯ)
Основная литература
| № п/п | Наименование | Автор(ы) | Год и место издания | Используется при изучении разделов | |
| 1. | Высшая математика для экономистов | Под ред. Н.Ш.Кремера | М.: ЮНИТИ, 2009 | 1-7 | |
| 2. | Высшая математика. | Зайцев И.А. | М.: Высшая школа,2005 г. | 1-7 | |
| 3. | Курс высшей математики для экономических вузов. | Карасев А.И. и др. | М.: Высшая школа, 2000 | 1-10 | |
| 4. | Краткий курс высшей математики | Кудрявцев В.А., Демидович Б.П. | М.: Наука, 2007. | 1-7 | |
| 5. | Сборник задач по высшей математике | Минорский В.П. | М.: Наука, 2008 | 1-7 | |
| 6. | Основы высшей математики. Учебное пособие для вузов. | Щипачев В.С., под ред. Тихонова А.Н. | М.: Высшая школа, 2008 | 1-8 | |
| 7. | Сборник задач по высшей математике | Под ред.Федина Н.А. | М.: Айриспресс, 2007. | 1-7 |
Дополнительная литература
| № п/п | Наименование | Автор(ы) | Год и место издания | Используется при изучении разделов | |
| 1. | Курс высшей математики | Баврин И.И.. | М.: Просвещение, 1993 | 1-7 | |
| 2. | Основы математического анализа | Ильин В.А., Позняк Э.Г. | М.: Наука, 2004 | 4-6 | |
| 3. | Линейная алгебра и некоторые ее приложения | Головина Л.И. | М.: Наука, 2005 | 1-2 | |
| 4. | Линейная алгебра. | Ильин В.А.,Позняк Э.Г. | М.: Наука, 1988 | ||
| 5. | Математический анализ | Мордкович А.Г., Солодовников А.С. | М.: Высшая школа, 1990 | 5-7 | |
| 6. | Курс высшей математики. Линейная алгебра. Аналитическая геометрия. Дифференциальное исчисление функции одной переменной. | Мантуров О.В., Матвеев Н.М. | М.: Высшая школа, 2005 | 1-7 | |
| 7. | Математика. Учебник. | Кузнецов Б.Г.. | М.: ЮНИТИ-ДАНА, 2004 | 1-7 | |
| 8. | Сборник задач по высшей математике. Часть 1,2. | Лунгу К.Н. и др.. | М.: Айрис-пресс, 2008 | 1-7 |
МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ (МОДУЛЯ)
Лекционные аудитории, оснащённые микрофоном и мультимедийными средствами обучения.
Курс лекций «Математика»
Предел функции.
Число A называется пределом функции 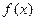 при
при 
 , если
, если 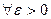
 , если
, если  .
.
Свойства пределов.
Пусть  ,
, 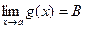 ,
,  , где A,B,C-конечные числа; a-число или один из символов
, где A,B,C-конечные числа; a-число или один из символов  .
.
Тогда 1) 
2) 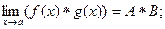
3)  , если
, если 
4)  если
если  .
.
Первый замечательный предел: 
Второй замечательный предел:  .
.
Функция  называется бесконечно малой при
называется бесконечно малой при 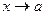 , если
, если 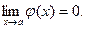 Функция
Функция  называется бесконечно большой при
называется бесконечно большой при 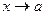 , если
, если 
Бесконечно малые при 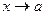 функции
функции  и
и  называются эквивалентными, если
называются эквивалентными, если  (обозначение
(обозначение  ). Функция
). Функция  является функцией более высокого порядка малости по сравнению с функцией
является функцией более высокого порядка малости по сравнению с функцией  при
при 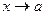 , если
, если  (обозначение
(обозначение  ).
).
Функция  называется непрерывной в точке
называется непрерывной в точке 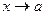 , если
, если 
Свойства непрерывных функций:
Пусть функции 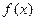 и
и  непрерывны в точке a. Тогда:
непрерывны в точке a. Тогда:
1) в точке a непрерывны функции:  ,
,  ,
,  ;
;
2) если  , то существует окрестность точки a, где
, то существует окрестность точки a, где  ;
;
3) если 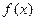 непрерывна в каждой точке отрезка
непрерывна в каждой точке отрезка  , то
, то
а) она ограничена
б) достигает своего максимального M и минимального m значений
в) принимает на этом отрезке любое значение 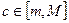
4) если  непрерывна в точке a, а
непрерывна в точке a, а 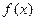 непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция  непрерывна в точке a.
непрерывна в точке a.
Пример 1. Найти предел: 
 .
.
Решение. Подстановка предельного значения аргумента в заданную функцию приводит к неопределенности вида  . Чтобы раскрыть эту неопределенность, используем тождественные преобразования функции:
. Чтобы раскрыть эту неопределенность, используем тождественные преобразования функции:

Ответ:  .
.
Пример 2. Найти предел:  .
.
Решение. Подстановка предельного значения аргумента в заданную функцию приводит к неопределенности вида  . Чтобы раскрыть эту неопределенность, сделаем замену переменных:
. Чтобы раскрыть эту неопределенность, сделаем замену переменных:  , тогда
, тогда 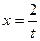 , если
, если  , то
, то  .
.

Ответ:  .
.
Упражнения.
Найти предел функции.
1.1.  при а)х0 = -2; б)х0 = 1; в) х0 = ¥
при а)х0 = -2; б)х0 = 1; в) х0 = ¥
1.2.  при а)х0 = 2; б)х0 = 5 в)х0 = ¥
при а)х0 = 2; б)х0 = 5 в)х0 = ¥
1.3.  .
.
1.4.  . 1.5.
. 1.5. 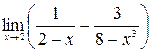 .
.
1.6.  . 1.7.
. 1.7.  .
.
1.8.  . 1.9.
. 1.9.  .
.
1.10.  . 1.11.
. 1.11.  .
.
1.12.  . 1.13.
. 1.13.  .
.
1.14.  . 1.15.
. 1.15.  .
.
1.16.  . 1.17.
. 1.17.  .
.
1.18.  . 1.19.
. 1.19.  .
.
1.20.  . 1.21.
. 1.21. 






