Если каждой паре (x, y) 
D по некоторому закону ставится в соответствие определенное значение z E, то говорят, что на множестве D задана функция двух переменных z = f(x, y).
(x, y) называются независимыми переменными (аргументами); z – зависимая переменная (функция),
D – область определения функции z, т. е. множество всех значений (x, y), при которых функция существует, имеет смысл.
E – область значений функции.
Уравнение z = f(x, y) описывает поверхность в пространстве, область D – фигура на плоскости.
Для функции z = f(x, y) можно составить три вида приращений:
1) частное приращение по аргументу x
,
2) частное приращение по аргументу y
,
3) полное приращение
.
Если существует конечный предел отношения частного приращения функции к приращению соответствующего аргумента при условии, когда последнее стремится к нулю, то этот предел называется частной производной по соответствующему аргументу и обозначается
.
Полным дифференциалом функции называется величина
,
где dx и dy – дифференциалы независимых переменных.
Градиент функции z(x, y):
.
Производная функции z(x,y) по направлению вектора 
: 
равна проекции вектора grad z на направление вектора . В направлении градиента происходит быстрое возрастание функции в данной точке.
Уравнение касательной плоскости к поверхности Ф(x,y,z)=0 в точке 
имеет вид:
.
Дивергенция вектора 
.
Ротор вектора
.
Вторыми частными производными функции z=z(x,y) называются частные производные от ее частных производных.
(другие обозначения 
). Смешанные производные 
и 
равны, если они непрерывны.
Экстремум функции нескольких переменных.
Необходимое условие: Если 
является точкой экстремума функции z=f(x, y), то ее частные производные первого порядка в этой точке равны нулю или не существуют.
Точки, удовлетворяющие этой системе, называются критическими.
Достаточное условие:
Если в критической точке (x0, y0) функции z = f(x,y) существуют и непрерывны производные
и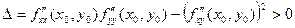 
, то эта точка является точкой минимума при 
,
максимума при 
. Если 
, то критическая точка не является точкой экстремума.
Координаты точек условного минимума (максимума) функции z = f(x,y) при условии 
удовлетворяют системе уравнений 
,
где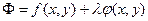 
- функция Лагранжа, 
- множитель Лагранжа.
Пример: Исследовать на экстремум функцию 
.
Решение: Найдем частные производные 
, 
.
Приравнивая их к нулю, получим систему 
,
из решения которой определим критическую точку (-3; 0). Найдем вторые частные производные: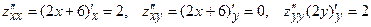 
.
Тогда 
, следовательно функция z в точке (-3; 0) имеет минимум равный 
.
Ответ: zmin=-13 при x=-3, y=0.
Упражнения.
3.1. Найти уравнения и выполнить построение линий уровня функции:
a) 
; b) 
;
c) 
;
d) 
; e) ;
f)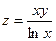 
.
3.2. Найти частные производные функции:
a) 
; b) 
;
c) 
; d) 
;
e) 
; f) 
;
g) 
; h) 
.
3.3. Найти экстремум функций:
a) 
; b) 
;
c) 
; d) ;
e) 
;
f) 
.
