1. Вычислите:
а. 
;
б. 
;
в. 
.
2. Встретились несколько человек и стали здороваться друг с другом. Известно, что рукопожатий было от 60 до 70. Сколько человек встретились, если известно, что:
а. каждый здоровался с каждым;
б. только один человек не здоровался ни с кем;
в. только двое не поздоровались между собой;
г. четверо поздоровались только между собой.
3. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля?
4. «Вороне где-то Бог послал кусочек брынзы, колбасы, сухарика и шоколада. На ель Ворона взгромоздясь, позавтракать совсем уж было собралась, да призадумалась»:
а. если есть кусочки по очереди, то из скольких вариантов придётся
выбирать;
б. сколько получится «бутербродов» из двух кусочков (бутербродом
считать набор из двух кусочков);
в. если съесть сразу три кусочка, а оставшийся спрятать, то из скольких
вариантов придётся выбирать;
г. сколько получится вариантов, если какой-то кусочек всё-таки бросить Лисе, а потом ответить на вопрос пункта a.
Раздел 11. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
1. Девять учащихся получили за зачет оценки: 3, 1, 2, 2, 4, 4, 5, 3, 4.
а. отразите данные на круговой и на столбчатой диаграмме;
б. найдите размах, моду и медиану ряда оценок. Найдите среднее арифметическое полученных оценок;
в. последовательно выписываются фамилии указанных девяти учащихся. Сколько есть способов составить список? Какова вероятность того, что при том, что список составляется случайным образом, первым в нем окажется тот, кто лучше всех написал эту контрольную?
г. определите вероятность того, что случайно выбранный учащийся этой группы получил тройку;
д. Перед контрольной каждый из учащихся наобум написал какую-то цифру от «1» до «5». Определите вероятность того, что каждый из них угадал полученную впоследствии оценку.
2. Случайным образом выбрали двузначное число. Найдите вероятность того, что оно:
а. оканчивается нулем;
б. состоит из одинаковых цифр;
в. больше 72 и меньше 87;
г. не является кубом целого числа.
3. Найдите вероятность того, что при бросании двух кубиков в сумме выпадет больше десяти очков.
4. На каждой грани правильного тетраэдра написана одна из цифр 1, 2, 3, 4 (цифры не повторяются). Тетраэдр бросают дважды. Найдите вероятность того, что оба раза он упадет на грань с одной и той же цифрой.
Раздел 12. УРАВНЕНИЯ И НЕРАВЕНСТВА.
1. Равносильны ли уравнения:
а. 
и 
;
б. 
и 
;
в. 
и 
.
2. Решите уравнения:
а.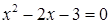 
;
б. 
;
в. 
;
г. 
;
д.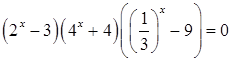 
;
е.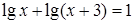 
;
ж. 
;
з.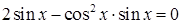 
;
и. 
.
3. Решите неравенства:
а. 
;
б. 
;
в. 
;
г. 
;
д. 
;
е.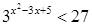 
;
ж. 
;
з.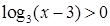 
.
4. Решите системы уравнений:
а. 
(методом алгебраического сложения)
б. 
(графическим методом)
в.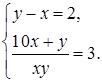 
(методом подстановки)
Вопросы для подготовки к экзамену
1. Прямые, плоскости и углы в пространстве
- взаимное расположение прямых и плоскостей в пространстве;
- основные теоремы стереометрии (признаки параллельности и перпендикулярности прямых и плоскостей, теорема о трех перпендикулярах);
- угол между прямой и плоскостью;
- угол между плоскостями, линейный угол двугранного угла.
2. Основы тригонометрии
- радианная мера угла;
- определения синуса, косинуса, тангенса и котангенса числа;
- формулы приведения;
- основное тригонометрическое тождество, формулы сложения, двойного и половинного аргумента, понижения степени;
- определение арксинуса, арккосинуса, арктангенса и арккотангенса числа;
- решение простейших тригонометрических уравнений;
- тригонометрические функции, их свойства и графики.
3. Элементы комбинаторики
- комбинаторное правило умножения;
- формулы для подсчета числа перестановок, размещений и сочетаний.
4. Корни, степени, логарифмы
- степень с натуральным, целым и рациональным показателем, корень
n-ой степени;
- логарифм числа и его свойства;
- свойства и графики показательной, логарифмической и степенной функции;
- способы решения иррациональных, показательных и логарифмических уравнений, показательных и логарифмических неравенств.
5. Функции, их свойства и графики
- определение функции;
- область определения и множество значений;
- нули и промежутки знакопостоянства;
- четность, периодичность и монотонность;
- стационарные точки, точки экстремума и экстремумы;
- наибольшее и наименьшее значения;
- вертикальные и горизонтальные асимптоты.
6. Начала математического анализа
- понятие производной функции;
- правила дифференцирования функций;
- таблица производных;
- уравнение касательной к графику функции;
- понятие второй производной;
- точки перегиба и промежутки выпуклости;
- применение производной к исследованию функций (по схеме);
- наибольшее, наименьшее значение функции на отрезке;
- понятие первообразной функции;
- таблица первообразных;
- понятие определенного интеграла;
- вычисление площадей криволинейных трапеций (формула Ньютона-Лейбница).
7. Многогранники, поверхности и тела вращения
- изображение пространственных фигур на плоскости (призма, пирамида, цилиндр, конус, шар);
- вычисление объемов и площадей поверхностей пространственных фигур;
- правильные многогранники.
8. Элементы теории вероятностей и математической статистики
- основные понятия статистики (мода, медиана, размах, среднее арифметическое, частота);
- классическое определение вероятности;
- совместные, несовместные, зависимые, независимые события и их вероятности.
Демонстрационный вариант для подготовки к экзамену.
1. Найдите значение выражения 
.
2. Упростите выражение 
.
3. Решите неравенство 
.
4. Найдите площадь фигуры, ограниченной линиями 
.
5. Упростите выражение 
.
6. Найдите производную функции 
.
7. Решите уравнение 
.
8. Найдите наименьшее и наибольшее значение функции 
на отрезке 
.
9. Вычислите (7+5i)(2-3i).
10. Напишите уравнение касательной к графику функции 
в точке с абсциссой 
.
11. Решите уравнение 
.
12. В четырехугольной пирамиде MABCD основание – квадрат ABCD. Ребро MA перпендикулярно плоскости основания. AB= 
, MA=1. Найдите объем пирамиды и угол наклона ребра MB к плоскости основания.
13. В треугольной пирамиде MABC основание – треугольник ABC, угол A= 
. Ребро MA перпендикулярно плоскости основания. MA=1, AB=AC=1. Найдите объем пирамиды и угол наклона ребра MB к плоскости основания.
14. Решите уравнение 
.
15. Сколько различных двузначных чисел можно составить из цифр:
а. 1,2,3,4 без повторения цифр?
б. 0,2,4,6 без повторения цифр?
16. Антонио дважды бросает монету. Найдите вероятность того, что при первом броске у него выпал орел.
[1] Издания, отмеченные значком *, имеются в фондах библиотеки РГУП
