1. В клетки квадратной таблицы 2x2 произвольно ставят крестики и нолики.
а. сколькими способами можно заполнить эту таблицу?
б. в скольких случаях в левой нижней клетке будет стоять крестик?
в. в скольких случаях в верхней левой и нижней правой клетках будут разные значки?
г. решите задачи пунктов а), б) и в) для таблицы 3x3.
2. У Карлсона на обед – первое, второе, третье блюда и пирожное. Он обязательно начнёт с пирожного, а всё остальное съест в произвольном порядке. Найдите число возможных вариантов обеда.
3. Одиннадцать футболистов строятся перед началом матча. Первым становится капитан, вторым - вратарь, а остальные - случайным образом. Сколько существует способов построения?
4. Игральный кубик бросают дважды и записывают выпадающие цифры.
а. найдите число всех возможных вариантов.
б. укажите те из них, в которых произведение выпавших чисел кратно 10.
5. Встретились 6 друзей и каждый пожал руку своему другу. Сколько было рукопожатий?
6. В классе 27 учеников. К доске нужно вызвать двоих. Сколькими способами это можно сделать, если:
а. первый ученик должен решить задачу по алгебре, а второй – по геометрии;
б. они должны быстро стереть с доски?
7. Отряд из 30 человек выбирает командира, заместителя командира и трёх помощников. Сколькими способами это можно сделать?
8. Из колоды в 36 карт вынимают 5 карт. Найдите:
а. число всех возможных вариантов выбора;
б. число вариантов, при которых среди полученных карт есть 4 туза;
в. число вариантов, при которых все полученные карты – пики;
г. число вариантов, при которых все полученные карты – одной масти.
9. По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выбрать двух дежурных по классу. Сколькими способами это можно сделать:
а. при условии, что пару обязательно должны составить мальчик и девочка;
б. без указанного условия?
Раздел 11. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
Вероятность
1. Найти вероятность того, что при двукратном бросании игрального кубика произведение выпавших очков будет:
а. кратно 10;
б. кратно 3.
2. Из колоды в 36 карт случайным образом вытаскивают 6 карт. Какова вероятность того, что среди выбранных карт будет хотя бы одна карта бубновой масти?
3. В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров ровно 3 белых?
4. Случайным образом выбрали двузначное число. Найдите вероятность того, что оно:
а. оканчивается нулём;
б. состоит из одинаковых цифр;
в. больше 27 и меньше 46;
г. не является квадратом целого числа.
5. Двузначное число составили из цифр 0, 1, 2, 3, 4. Какова вероятность того, что это число:
а. чётное;
б. нечётное;
в. делится на 5;
г. делится на 4?
6. Во все клетки квадратной таблицы 2x2 произвольно ставят крестики и нолики. Найдите вероятность того, что:
а. будет поставлен ровно один крестик;
б. будут поставлены ровно два нолика;
в. в левой нижней клетке будет стоять крестик;
г. в верхней левой и нижней правой клетках будут разные значки.
7. Игральную кость бросили дважды. Найдите вероятность того, что:
а. среди выпавших очков есть хотя бы одна единица;
б. сумма выпавших очков больше трёх;
в. сумма выпавших очков меньше 11;
г. произведение выпавших очков меньше 27.
8. Из костей домино случайно выбрали одну. Найдите вероятность того, что:
а. она не является дублем;
б. на ней не выпала «тройка»;
в. произведение очков на ней меньше 29;
г. модуль разности очков больше единицы.
9. Случайно нажимают на клавиши одной октавы. Найдите вероятность того, что:
а. звучат ноты «си» и «до»;
б. не звучит нота «фа»;
в. звучит нота «ля»;
г. получится до-мажорное трезвучие.
Раздел 12. УРАВНЕНИЯ И НЕРАВЕНСТВА.
Иррациональные уравнения.
Решите уравнения, системы уравнений:
1.  ;
;
2. 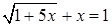 ;
;
3.  ;
;
4.  ;
;
5. 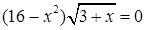 ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12.  ;
;
13.  ;
;
14.  ;
;
Логарифмические уравнения
Решите уравнение:
1.  ;
;
2. 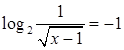 ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9. 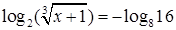 ;
;
10.  .
.
Показательные уравнения.
Решите уравнения, системы уравнений:
1.  ;
;
2.  ;
;
3. 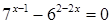 ;
;
4.  ;
;
5.  ;
;
6. 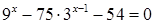 ;
;
7.  ;
;
8.  ;
;
9.  ;
;






