Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Задача.
Боковая грань правильной треугольной пирамиды представляет собой правильный треугольник, площадь которого 16 корней из 3 см2 (16√3). Вычислить периметр основания пирамиды.
Решение.
Правильный треугольник - это равносторонний треугольник. Соответственно, боковая грань пирамиды представляет собой равносторонний треугольник.
Площадь равностороннего треугольника равна:

Соответственно:
16√3 = a2 √3 / 4
16 = a2 / 4
a2 = 64
a = 8 см
Основанием правильной треугольной пирамиды является правильный (равносторонний) треугольник. Таким образом, периметр основания пирамиды равен
8 * 3 = 24 см
Ответ: 24 см.
Задача.
В правильной треугольной пирамиде высота равна 10 см, а сторона основания 16 см. Найти площадь боковой поверхности.
Решение.
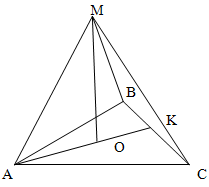
Поскольку основанием правильной треугольной пирамиды является равносторонний треугольник, то AO является радиусом описанной вокруг основания окружности.
(Это следует из свойств правильной пирамиды)
Радиус окружности, описанной вокруг равностороннего треугольника найдем из его свойств

Откуда длина ребер правильной треугольной пирамиды будет равна:
AM2 = MO2 + AO2
высота пирамиды известна по условию (10 см), AO = 16√3/3
AM2 = 100 + 256/3
AM = √(556/3)
Каждая из сторон пирамиды представляет собой равнобедренный треугольник. Площадь равнобедренного треугольника найдем как

S = 1/2 * 16 sqrt((√(556/3) + 8) (√(556/3) - 8))
S = 8 sqrt((556/3) - 64)
S = 8 sqrt(364/3)
S = 16 sqrt(91/3)
Поскольку все три грани у правильной пирамиды равны, то площадь боковой поверхности будет равна
3S = 48 √(91/3)
Ответ: 48 √(91/3)
Правильная пирамида с треугольником в основании (часть 2)
Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Задача
В правильной треугольной пирамиде боковые грани наклонены к основанию под углом 60 градусов. Расстояние от центра основания до боковой грани равно 2√3. Найти объём пирамиды.
Решение.
Основанием правильной треугольной пирамиды по определению является равносторонний треугольник. А расстояние от центра основания до боковой грани равно радиусу вписанной окружности. Согласно свойствам равностороннего треугольника площадь основания равна:

S = 3√3 r2 = 3√3 (2√3)2 = 36√3

Поскольку грани наклонены к основанию под углом 60 градусов, то для прямоугольного треугольника MOK
tg MKO = MO/KO
tg 60 = MO / (2√3)
Исходя из таблицы значений тригонометрических функций tg 60 = √3
√3 = MO / (2√3)
MO = 6
Таким образом, высота пирамиды равна 6 см.
Объем пирамиды найдем по формуле:
S = 1/3 Sh
S = 1/3 * 36√3 * 6
S = 72√3
Ответ: 72√3
Задача
Сторона правильной треугольной пирамиды равна 3 см а угол между боковой гранью и основанием пирамиды равен 45 градусов. Найдите площадь полной поверхности пирамиды.
Решение.
Поскольку пирамида правильная, в ее основании лежит равносторонний треугольник. Поэтому площадь основания равна

So = 9 * √3/4

Для того, чтобы найти площадь боковой грани, вычислим высоту KM. Угол OKM по условию задачи равен 45 градусам.
Таким образом:
OK / MK = cos 45
Воспользуемся таблицей значений тригонометрических функций и подставим известные значения.
OK / MK = √2/2
Учтем, что OК равен радиусу вписанной окружности.
Тогда (по таблице соотношений в правильном треугольнике)
OK = √3/6 a
OK = √3/6 * 3 = √3/2
Тогда
OK / MK = √2/2
√3/2 / MK = √2/2
MK = √3/√2
Площадь боковой грани тогда равна половине произведения высоты на основание треугольника.
Sбок = 1/2 * 3√(3/2)
Откуда площадь полной поверхности будет равна
S = 9√3/4 + 3/2 √(3/2)
Правильная пирамида с треугольником в основании (часть 3)
Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Задача.
Высота основания правильной треугольной пирамиды равна 3 см. а угол между боковой гранью и основанием пирамиды равен 45 градусов.Надо найти площадь полной поверхности пирамиды
Решение.

В основании правильной треугольной пирамиды лежит равносторонний треугольник.
Поэтому для решения задачи воспользуемся свойствами правильного треугольника:

Нам известна высота треугольника, откуда можно найти его площадь.
h = √3/2 a
a = h / (√3/2)
a = 3 / (√3/2)
a = 6 / √3
Откуда площадь основания будет равна:
S = √3/4 a2
S = √3/4 (6 / √3)2
S = 3√3
Для того, чтобы найти площадь боковой грани, вычислим высоту KM. Угол OKM по условию задачи равен 45 градусам.
Таким образом:
OK / MK = cos 45
Воспользуемся таблицей значений тригонометрических функций и подставим известные значения.
OK / MK = √2/2
Учтем, что OК равен радиусу вписанной окружности. Тогда
OK = √3/6 a
OK = √3/6 * 6/√3 = 1
Тогда
OK / MK = √2/2
1 / MK = √2/2
MK = 2/√2
Площадь боковой грани тогда равна половине произведения высоты на основание треугольника.
Sбок = 1/2 (6 / √3) (2/√2) = 6/√6
Таким образом, площадь полной поверхности пирамиды будет равна
S = 3√3 + 3 * 6/√6
S = 3√3 + 18/√6
Ответ: 3√3 + 18/√6
Правильная пирамида с треугольником в основании (часть 4)
Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Задача.
Высота правильной треугольной пирамиды 4 см, а ее апофемы 8 см.
Вычислите площадь боковой поверхности пирамиды.
Решение.

Исходя из того, что MK = 8, MO = 4, синус угла OKM равен
MO/MK = 1/2
откуда угол равен arcsin 1/2 = 30 градусов.
Откуда
KO / MK = cos 30
KO / 8 = cos 30
KO = 8 cos 30
По таблице тригонометрических функций найдем значение косинуса 30 градусов.
KO = 8√3/2 = 4√3
Учтем, что KO является радиусом вписанной окружности в основание правильной треугольной пирамиды (согласно свойствам правильной пирамиды). Тогда по свойству равностороннего треугольника

r = a√3/6
Подставим в формулу известное нам значение радиуса вписанной окружности, откуда найдем значение стороны равностороннего треугольника
4√3 = a√3/6
a = 24
Теперь, зная размер основания боковой грани и ее апофему, найдем площадь боковой грани как площадь равнобедренного треугольника:
Sт = 1/2 * 24 * 8 = 96 см2
Откуда площадь боковой поверхности пирамиды
S = 3 Sт = 3 * 96 = 288 см2.
Ответ: 288 см2.
Правильный тетраэдр (пирамида)
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Теория
(теоретические сведения см. также в уроке "Правильный тетраэдр")
Правильный тетраэдр - это правильная треугольная пирамида у которой все грани являются равносторонними треугольниками.
У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны
У тетраэдра 4 грани, 4 вершины и 6 ребер.
Основные формулы для правильного тетраэдра приведены в таблице.

Где:
S - Площадь поверхности правильного тетраэдра
V - объем
h - высота, опущенная на основание
r - радиус вписанной в тетраэдр окружности
R - радиус описанной окружности
a - длина ребра
Практические примеры






