Решение.
Поскольку все ребра треугольной пирамиды равны - она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a2√3.
Тогда
S = 3√3
Ответ: 3√3
Задача.
Все ребра правильной треугольной пирамиды равны 4 см. Найдите объем пирамиды
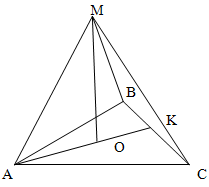
Решение.
Поскольку в правильной треугольной пирамиде высота пирамиды проецируется в центр основания, который одновременно является центром описанной окружности, то
AO = R = √3 / 3 a
AO = 4√3 / 3
Таким образом, высота пирамиды OM может быть найдена из прямоугольного треугольника AOM
AO2 + OM2 = AM2
OM2 = AM2 - AO2
OM2 = 42 - (4√3 / 3)2
OM2 = 16 - 16/3
OM = √(32/3)
OM = 4√2 / √3
Объем пирамиды найдем по формуле V = 1/3 Sh
При этом площадь основания найдем по формуле S = √3/4 a2
V = 1/3 (√3 / 4 * 16) (4√2 / √3)
V = 16√2 / 3
Ответ: 16√2 / 3 см
С четырехугольником в основании
Пирамида
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение.
Задача
Длина стороны ромба ABCD равна 5 см, длина его диагонали BD равна 6 см. Через точку О, которая является точкой пересечения диагоналей ромба, проведена прямая OK, перпендикулярная его плоскости. Найти расстояние от точки К до вершин ромба (КА, КВ, КС, КD) если ОК = 8см.
Решение.
В результате построения геометрической фигуры по условию задачи, заметим, что у нас получилась пирамида, в основании которой лежит ромб. Нам необходимо найти величину ребер пирамиды, которые прилегают к ее вершине.
Поскольку диагонали ромба делятся в точке пересечения пополам, то BO равно половине диагонали BD.
BO = BD / 2 = 6 / 2 = 3 см
Поскольку OK по условию задачи является перпендикуляром к плоскости основания пирамиды, то треугольник BOK является прямоугольным. Отсюда, по теореме Пифагора находим величину ребра BK.
BK2 = BO2 + OK2
BK2 = 32 + 82
BK2 =73
BK = sqrt (73), то есть корень квадратный из 73
Поскольку треугольники BKO и DKO равны по двум сторонам и углу (KO - общая сторона треугольников, BO=OD как половины диагонали ромба, а прямой угол образован перпендикуляром по условию задачи), то ребро BK = BD.
Вычислим длину ребра AK. Поскольку диагонали ромба пересекаются под прямым углом, то зная величину половины одной диагонали и стороны ромба, несложно определить величину половины другой диагонали, то есть:
AB2 = BO2 + AO2
52 = 32 + AO2
AO2 = 52 - 32
AO2 = 16
AO = 4
Аналогичным способом теперь найдем длину ребра AK
AK2 = AO2 + OK2
BK2 = 42 + 82
BK2 = 80
BK = 4 sqrt(5), четыре квадратных корня из пяти
Поскольку треугольники AOK и COK также равны по двум сторонам и углу, то AO = CO.
Ответ: AO и CO равны четыре квадратных корня из пяти, а BO и DO равны корню квадратному из 73
Задача
Высота четырехугольной пирамиды равна 4см. а её апофема создаёт с высотой угол 45 градусов.Найдите боковую поверхность пирамиды.
Решение.
Исходя из того, что по условию задачи любая апофема создаёт с высотой угол 45 градусов, то пирамида является правильной. Площадь боковой поверхности правильной пирамиды - S = 1/2 Pa, где P - периметр основания, a - апофема боковой грани. Апофема образует с высотой пирамиды и отрезком, проведенным из точки пересечения высоты и основания на сторону основания прямоугольный треугольник. Это следует из определения высоты пирамиды - она образует с плоскостью основания прямой угол.
Данный треугольник является равнобедренным, поскольку сумма углов треугольника равна 180 градусам, один из углов прямой, тогда 180 - 90 - 45 = 45. Поскольку оба угла равны - треугольник равнобедренный.
Таким образом, длина стороны основания равна удвоенной высоте пирамиды (треугольник равнобедренный, поэтому второй катет равен высоте пирамиды, а он же равен половине стороны, поскольку пирамида является правильной).
Исходя из того, что оба катета треугольника, образованного высотой пирамиды и отрезком, проведенным к боковой грани равны, то по теореме Пифагора апофема пирамиды равна
a = sqrt(42 + 42) = sqrt(32) = 4 sqrt(2), четыре корня из двух
Периметр равен 4 * 2 * 4 = 32 см, таким образом
S = 1/2 Pa = 1 / 2 * 32 * 4 sqrt(2) = 64 sqrt(2), 64 корня из двух
Ответ: 64 корня из двух
Задача
Диагональ основания правильной четырехугольной пирамиды равна 24 см,а боковое ребро равно 26 см. Найти: а) площади диагонального сечения пирамиды б) сторону основания пирамиды в) площадь боковой поверхности пирамиды.
Решение.
Поскольку пирамида правильная, то диагональ основания вместе с соответствующими двумя ребрами пирамиды образуют равнобедренный треугольник, площадь которого будет равна площади диагонального сечения пирамиды. Его площадь можно найти по формуле Герона:
S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S = 1/4 sqrt((26 + 26 + 24)(26 + 24 - 26)(26 + 24 - 26)(26 + 26 - 24))
S = 1/4 sqrt(76 * 24 * 24 * 28) = 1/4 sqrt(1225728) ≈ 276, 78 см2.
Поскольку пирамида правильная, то ее диагональ образует с двумя сторонами основания равнобедренный прямоугольный треугольник. Если обозначить сторону основания как а, то по теореме Пифагора
а2 + а2 = 242
2а2 = 576
а2 = 288
а = sqrt(288) ≈ 16.97 см
Площадь боковой поверхности пирамиды будет равна сумме площадей поверхностей боковых граней, каждая из которых по формуле Герона имеет площадь
S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S = 1/4 sqrt((26 + 26 + sqrt(288))(26 + sqrt(288) -26)(26 + sqrt(288) -26)(26 + 26 - sqrt(288)))
S = 1/4 sqrt(695808) ≈ 208.54 см2.
То есть площадь боковой поверхности будет равна 4S = sqrt(695808) ≈ 208.54 см2.
Ответ: 1/4 sqrt(1225728) см2, sqrt(288) см, sqrt(695808) см2.






