Примечание. В данном уроке изложены задачи по геометрии о площади поверхности цилиндра. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Почти наверняка курс будет дополнен.
Задача.
Какой из цилиндров с обьемом 128π см3 имеет наименьшую полную поверхность?
Решение.
Формула нахождения объема цилиндра
V = πr2 h
Поскольку объем цилиндра нам известен, то
πr2 h = 128π
откуда
r2 h = 128
h = 128 / r2
Площадь полной поверхности цилиндра равна площади его оснований и площади боковой поверхности. Таким образом, формула площади поверхности цилиндра будет выглядеть следующим образом:
S = 2πr2 + 2πrh
где
πr2 - площадь основания цилиндра (площадь круга)
2πr - длина окружности основания
Подставим значение высоты цилиндра в полученную формулу
S = 2πr2 + 2πrh
S = 2πr2 + 2πr * 128 / r2
S = 2πr2 + 256π / r
Если представить полученную формулу как функцию площади заданного в задаче цилиндра, то минимальная площадь цилиндра будет достигнута в точке экстремума данной функции. Для нахождения экстремума дифференцируем полученную функцию.
f(r) = 2πr2 + 256π / r
Формулы дифференцирования можно посмотреть в таблице производных. Получим:
f '(r) = 4πr - 256π / r2
Поскольку в точке экстремума производная функции равна нулю, приравняем f '(r) к нулю и решим уравнение.
4πr - 256π / r2 = 0
получим
4πr (1 - 64/r) = 0
откуда
4πr = 0 или 1 - 64/r = 0
первый найденный корень уравнения r = 0 отбрасываем,
1 - 64/r = 0
r = 64
Откуда
h = 128 / r2
h = 128 / 4096
h = 0.03125 или 1/32
Ответ: минимальная площадь цилиндра будет достигнута при h = 1/32 см, r =64 см
Конус
Конус
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
Задача
Объем цилиндра равен 48 см3. Найти объем конуса, радиус основания которого равна радиусу основания цилиндра, а высота вдвое меньше высоты цилиндра.
Решение.
Формула объема цилиндра
V = hпr2
А формула объема вписанного конуса (V = 1/3hпr2) для "нашего" случая, учитывая, что высота конуса равна половине высоты цилиндра, будет равна:
V = 1/3 h/2 пr2
но, по условию задачи, объем цилиндра составляет 48, то есть hпr2 = 48. Значит подставим в формулу объема конуса вместо hпr2 известное нам значение. Получаем:
V = 1/3 * 48 / 2
V = 8 см3.
Ответ: 8 см3.
Задача
Высота конуса равна 5см, а радиус основания 12см. Найдите площадь полной поверхности конуса.
Решение.
Примечание. Для обозначения символа извлечения квадратного корня в данной задаче используется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках - подкоренное выражение.
Для нахождения площади поверхности конуса воспользуемся следующими формулами:
S1 = пrl - площадь боковой поверхности конуса, где r - радиус конуса, а l - длина образующей
S2 = пr2 - площадь круга, то есть основания конуса
Таким образом, площадь поверхности конуса составит
S = S1 + S2
Поскольку S1 = пrl, найдем образующую. Поскольку Высота конуса, радиус основания конуса и образующая являются сторонами прямоугольного треугольника, то
l2 = h2 + r2
S1 = пr * sqrt(h2 + r2)
Тогда
S1 + S2 = пr(h2 + r2) + пr2 = п * 12 * sqrt(25 + 144) + 144 * п = п * 12 * 13 + 144 * п = 156п + 144п = 300п ≈ 942,48
Ответ: 300п ≈ 942,48 см2.
Площадь боковой поверхности конуса
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, конус). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
Задача.
Площадь основания конуса 36π см2, а его образующая 10 см.
Вычислить боковую поверхность конуса.
Решение.
Зная площадь основания, найдем его радиус.
S = πR2
36π = πR2
R2 = 36
R = 6
Площадь боковой поверхности конуса найдем по формуле:
S = πRl
где
R - радиус основания
l - длина образующей
откуда
S = π * 6 * 10 = 60π
Ответ: 60π см2.
Объем конуса
Примечание. Это урок с решениями задач по геометрии (раздел стереометрия, конус). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
Задача.
В цилиндр вписаны шар и конус, причём высота цилиндра равна диаметру его основания.
Найти отношение объёма конуса к объёму шара, и к объёму цилиндра.
Решение.
Для решения задачи воспользуемся формулами нахождения объема шара, цилиндра и конуса:
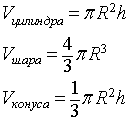
Учтем, что по условию задачи высота цилиндра, а, соответственно и конуса, равны диаметру шара, что следует из построения согласно условию. То есть шар касается обеих оснований цилиндра в их центре. Из чего запишем:
h = 2R
Откуда
Vцилиндра = πR2h = πR22R = 2πR3
Vшара = 4/3πR3
Vконуса = 1/3πR2h = 1/3πR22R = 2/3πR3
Таким образом, соотношение объема конуса к объему шара будет равно:
Vконуса / Vшара = 2/3πR3 / 4/3πR3 = 2/3 / 4/3 = 1/2
А соотношение объема конуса к объему цилиндра будет равно:
Vконуса / Vшара = 2/3πR3 / 2πR3 = 2/3 / 2 = 1/3
Ответ: 1/2 и 1/3
Задача.
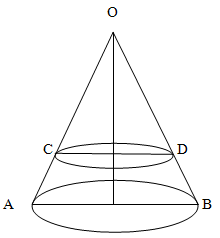
Объем конуса равен 27. На высоте конуса лежит точка и делит её в отношении 2:1 считая от вершины. Через точку проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение.
Обратим внимание, что треугольники AOB и COD - подобны. Из условия задачи определим коэффициент подобия как 2:3.
Объем конуса находится по формуле, указанной в предыдущей задаче.
Vконуса = 1/3πR2h = 27 (по условию)
Тогда объем малого конуса будет равен
Vмал.конуса = 1/3π(2/3R)2(2/3h)
то есть
Vмал.конуса = 1/3π 4/9 R2 2/3 h
Vмал.конуса = 8/27 *1/3π R2 h
а так как мы знаем, что 1/3π R2 h= 27 (см. выше), то
Vмал.конуса = 8/27 * 27 = 8
Ответ: объем малого конуса равен 8
Объем конуса (2)
Примечание. Это урок с решениями задач по геометрии (раздел стереометрия, конус). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
Задача
Образующая конуса равна 12 см. Угол между образующей и плоскостью основания равен 30 градусов. Найти объем конуса.
Решение.

Объем конуса найдем по формуле:
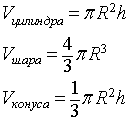
Поскольку образующая вместе в высотой конуса и радиусом его основания образуют прямоугольный треугольник, то необходимые размеры конуса вычислим исходя из того, что нам известен угол этого прямоугольного треугольника между основанием и образующей конуса.
h / OB = sin 30
h = OB sin 30
h = 12 sin 30
По таблице значений тригонометрических функций найдем значение синуса 30 градусов.
h = 12 * 1/2
h = 6
R / OB = cos 30
R = OB cos 30
R = 12 cos 30
По таблице значений тригонометрических функций найдем значение косинуса 30 градусов.
R = 12 √3/2
R = 6√3
Откуда объем конуса будет равен:
V = 1/3π (6√3)2 * 6
V = 216π
Ответ: объем конуса равен 216π см2.






