Сходимость или расходимость знакоположительного ряда часто устанавливается путем сравнения его с другим рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.
Теорема 1: пусть даны два знакоположительных ряда 
и 
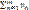. Если для всех n выполняется неравенство un≤vn, то из сходимости ряда 
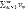следует сходимость ряда 
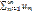, из расходимости 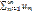следует расходимость ряда .
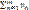Доказательство 1: обозначим n-е частичные суммы рядов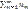 
и 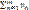соответственно через S(u)n и S(v)n. Из неравенства un≤vn следует, что S(u)n ≤ S(v)n. Пусть ряд и 
сходится и его сумма равна S2. Тогда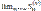 
= S2.Члены ряда 
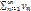положительны, поэтому S(v)n< S2 и, следовательно, с учетом неравенства S(u)n ≤ S(v)n, S(u)n ≤ S2. Таким образом, последовательность S(u)1, S(u)2, S(u)n,… монотонно возрастает (un>0) и ограниченно сверху числом S2. По признаку существования предела последовательность {S(u)n}имеет придел 
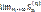=S1, т.е. ряд 
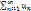сходится. Пусть теперь ряд 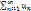расходится. Так как члены ряда неотрицательны, в этом случае имеем 
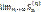=∞. Тогда, с учетом неравенства S(u)n ≤ S(v)n, получаем 
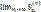=∞, т.е. ряд 
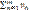расходится.
Теорема 2 (предельный признак сравнения): пусть даны два знакоположительных ряда и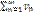 
. Если существует конечный, отличный от 0, предел 
=A (0<A<∞), то ряды 
и 
сходятся или расходятся одновременно.
Доказательство 2: по определению предела последовательности для все n, кроме, возможно, конечного числа их, для любого ε>0 выполняется неравенство |un/vn-A|<ε, или (А-ε)vn<un<(A+ε)vn. Если ряд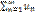 
сходится, то из левого неравенства (А-ε)vn<un<(A+ε)vn и теоремы 1 вытекает, что ряд 
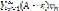также сходится. Но тогда, согласно свойству 1 числовых рядов, ряд 
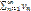сходится. Если ряд 
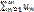расходится, то из правого неравенства (А-ε)vn<un<(A+ε)vn, теоремы 1, свойства 1, вытекает, что и ряд 
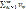расходится. Аналогично, если ряд 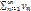сходится (расходится), то сходящимся (расходящимся) будет и ряд .
Признак Даламбера.
Теорема: пусть дан ряд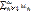 
=u1+u2+…+un+… с положительными членами и существует
конечный или бесконечный предел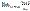 
=ℓ. Тогда ряд сходится при ℓ<1 и расходится при ℓ>1.
Так как 
=ℓ, то по определению предела для любого ε>0 найдется натуральное число N такое, что при n>N выполняется нера-
венство |un+1/un-ℓ|<ε или ℓ-ε<un+1/un<ℓ+ε.
Пусть ℓ<1. Можно подобрать ε так, что число ℓ+ε<1. Обозначи
м ℓ+ε=q, q<1. Тогда из правой части неравенства |un+1/un-ℓ|<ε или ℓ-ε<un+1/un<ℓ+ε получим un+1/un<
q, или un+1/<qun,n>N. В силу свойства 3 числовых рядов
можно считать, что un+1/<
qun
для всех n = 1,2,3,... Давая номеру n
эти значения, получим серию неравенств, т.е. члены ряда u2+u3+u4+…+un+… меньше соответствующих членов ряда qu1+q2u1+q3u1+…+qn+1u1+…, который сходится как ряд геометрической прогресии со знаменателем 0<q<1. Но тогда, на основании признака сравнения, сходится ряд u2+u3+u4+…+un+…, следовательно сходится и исходный ряд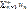 
=u1+u2+…+un+…
Пусть ℓ>1. В этом случае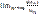 
=ℓ>1. Отсюда следует, что, начиная с некоторого номера N, выполняется неравенство un+1/un>1, или un+1>un, т.е. члены ряда возрастают с увеличением номера n. Поэтому 
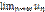≠0. На основании следствия из необходимого признака ряд 
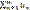=u1+u2+…+un+… расходится.
Замечания: 1. Если ℓ=1, то ряд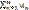 
=u1+u2+…+un+… может быть как сходящимся, так и расходящимся. 2. Признак Даламбера целесообразен применять, когда общий член ряда содержит выражения вида n! или an.
