Квадратичная форма — функция на векторном пространстве задаваемая однородным квадратным многочленом от координат.
Пусть L есть векторное пространство над полем K и{e1,e2,…,en} — базис в L.
Функция Q из L в K называется квадратичной формой если её можно представить в виде Q(x)= 
, где x=x1e1+x2e2+…+xnen=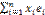 
, а aij элементы поля K.
Связанные определения: 1)Матрицу (aij) называют матрицей квадратичной формы в данном базисе. 1.1)В случае если характеристика поля K не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть aij = aji.
2)Для любой квадратичной формы Q существует единственная билинейная симметричная форма B, такая, что Q (x) = B (x, x) 2.1)Такую билинейную форму B называют полярной к Q. 2.2)Полярная форма может быть вычислена по формуле 4B(x,y)=Q(x+y)-Q(x-y). 2.3)Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
3)Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе — вырожденной.
4)Квадратичная форма Q называется положительно (отрицательно) определённой, если для любого x≠0 Q (x) > 0 (Q (x) < 0).
4.1)Положительно определённые и отрицательно определённые формы называются знакоопределёнными. 4.2)Квадратичная форма A (x, x) называется знакопеременной, если она принимает как положительные, так и отрицательные значения. 4.3)Квадратичная форма Q называется полуопределенной, если A(x,x)≥0 (A(x,x)≤0)..
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Критерий положительной определённости квадратичной формы
Доказательство критерия Сильвестра основано на методе Якоби приведения квадратичной формы к каноническому виду – для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны.
1. «Необходимо» Имеется положительно определённая квадратичная форма. j-ый диагональный элемент положителен, так как k(x)>0 в том числе и для вектора со всеми нулевыми координатами, кроме j-ой. 2. «Достаточно» Имеется положительность миноров. Первый минор определяет знак первого диагонального элемента в каноническом виде. Знак отношения Mi+1/Miопределяет знак i+1-ого элемента в диагональном виде. Так получим, что в каноническом виде все элементы на диагонали положительные, то есть квадратичная форма определена положительно.
Критерий отрицательной определённости квадратичной формы – для отрицательной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры чётного порядка её матрицы были положительны, а нечётного порядка — отрицательны.
Доказательство сводится к предыдущему случаю, так как матрица A является отрицательно определённой тогда и только тогда, когда матрица − A является положительно определённой. При замене матрицы A на противоположную главные миноры нечётного порядка меняют знак, а главные миноры чётного порядка остаются такими же.
Теорема (достаточное условие экстремума): пусть в стационарной точке (х0;у0) и некоторой ее окрестности функции f(х;у) имеет непрерывное частные производные до второго порядка включительно. Вычислим в точке (х0;у0) значения А=f’’хх(х0;у0)=0, В=f’’ху(х0;у0)=0, С=f’’уу(х0;у0). Обозначим ∆=АС-В2. Тогда: 1. если ∆>0, то функция f(х;у) в точке (х0;у0) имеет экстремум: максим, если А<0; минимум, если А>0: 2. если ∆<0, то функция f(х;у) в точке (х0;у0) экстремума не имеет. 3. в случае ∆=0 экстремум в точке (х0;у0) может быть, может и не быть. Необходимы дополнительные исследования. Теорема принимается без доказательства.
