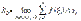Если P(z) и Q(z) – многочлены в комплексной области, то P(z)/Q(z) - рациональная дробь. Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q.
Любую неправильную дробь можно представить в виде:
P(z)/Q(z) = S(z) + R(z)/Q(z), где P(z) = Q(z) S(z) + R(z),a R(z) – многочлен, степень которого меньше степени Q(z).
Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как R(z)/Q(z) является правильной дробью.
Определение. Простейшими (или элементарными) дробями называются дроби следующих видов: 1) A/x-a, 2) A/(x-a)^n,
3) Ax+B/x^2 +px + q, 4) Ax+B/(x^2 +px + q)^n
Выясним, каким образом они интегрируются.
и 
Теорема. Всякую правильную дробь можно представить в виде суммы простейших дробей.
Следствие. Если P(z)/Q(z) - правильная рациональная дробь, и если среди корней многочлена Q(z) будут только простые действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го типа: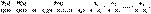 
Интегрирование некоторых тригонометрических функций и некоторых иррациональностей.
Интегралы вида ∫sin^m x ⋅ cos^n xdx.
а). Если хотя бы одно из чисел m или n – нечетное положительное чис-
ло, то, отделяя от нечетной степени один сомножитель и выражая с
помощью формулы sin^2 x + cos^2 x = 1 оставшуюся четную степень через
дополнительную функцию, переходим к табличному интегралу.
б). Если m и n – четные неотрицательные числа, то степени понижаются с помощью тригонометрических формул:
cos^2 x = 1+cos2x/2, sin^2 x = 1-cos2x/2, sinx cosx = ½* sin2x
Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла.
Задача о площади криволинейной трапеции.
О: Под криволинейной трапецией пониматся фигура D, которая имеет границу 
в данном случаеявляется f(x) является непрерывной. Вычислим площадь криволинейной трапеции. Для этого следует разделить отрезок [a,b] с помощью точек 
на n элементарных отрезков 
Отметим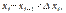 
определим случайные точкии 
отобразим ступенчатую фигуру, состоящую из прямоугольников с высотами 
и основаниями 
. Площадь ступенчатой фигурыи 
определяет приблизительное значение площади криволинейной трапеции. В качестве точного значения площади запишем 
