Предположим, что на [a,b] определена функция n частей 
и запишем сумму 
которая именуется интегральной.
О: Под определенным интегралом (о.и.) от функции 
и от выбора 
Обозначение: 
Числа f(x) именуют интегрируемой (по Риману) на [a,b].
Т. существования: При условии, что[a,b].
В соответствии с определением о.и. отметим, что интеграл имеет зависимость от вида f(x), пределов a и b, однако не зависит от символа обозначения переменной x, иначе выражаясь 
Св-ва определенного интеграла
Используя определение предела интегральных сумм, получаем следующие свойства определенного интеграла:
1) Если f(x) и g(x) 
, 
- произвольные числа, то функция 
и справедливо равенство: 
2) 
Если f(x) 
, то 
3) Если f(x) 
и c 
, то f(x) 
, f(x) 
и справедливо равенство: 
4) Если f(x) 
, 
и b>a, то справедливо неравенство: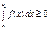 
5) Если f(x) и g(x) , 
и b>a, то справедливо неравенство: 
6) 
Если f(x) 
и 
, 
, b>a, то выполняются неравенства: 
7) 
Если f(x) 
, то 
, такое, что выполняется равенство: 
Интегрирование подстановкой и по частям в опред интеграле
Интегрирование подстановкой
Теорема. Если
То 
Пусть F(x) есть первообразная для f(x) на отрезке [a;b],
Интегрирование по частям
Теорема: если ф-ция u=u(x) имеют непрерывные производные на отрезке [a;b],то имеет место формула
Теорема о производной от интеграла по переменному верхнему пределу.
Если в определенном интеграле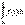 
изменять верхний предел b, то будет меняться и значение интеграла, то есть интеграл будет функцией верхнего предела.
Обозначим верхний предел x, а переменную интегрирования, чтобы не смешивать ее с верхним пределом, обозначим t. Таким образом, интеграл с переменным верхним пределом является функцией от x: 
Имеет место теорема: производная интеграла с переменным верхним пределом от непрерывной функции равна подынтегральной функции, в которой переменная интегрирования заменена верхним пределом: 
Доказательство. По определению производной
где 
[первый интеграл представим в виде суммы двух интегралов, пользуясь свойством аддитивности]=
[по теореме о среднем]= 
где 
Тогда 
следует из определения непрерывной функци, т.к. при 
Таким образом, 
Это значит, что интеграл с переменным верхним пределом 
является первообразной для функции f(x).
9. Формула Ньютона – Лейбница.
Сравнивая две формулы для площади криволинейной трапеции, приходим к следующему заключению: если F (x) - первообразная функции f (x) на отрезке [ a, b ], то
формула справедлива для любой функции f (x), непрерывной на отрезке [ a, b ].
Геометрические приложения определенных интегралов
