Общий вид F(x;y;y’)=0 e. Уравнения связывает переменную x, искомую функцию y и ее производную y’, то его записывают в виде y’=f(x;y) и называют ДУ первого порядка, разрешенным относительно производной. Диф. Уравнение 1-го порядка,разрешено относительно производной, можно записать в диф. Форме P(x;y)dx+Q(x;y)dy=0. Общ. Решения y=ϕ(x;c): 1) функц.ϕ(x;c) является решением ДУ при каждом фиксированном значении с.2)Каково бы ни было начальное условие можно найти такое значение постоянной с=сₒ, что функция y=ϕ(x;cₒ) удовлетворяет данному начальному условию. Частным решением ДУ:1)назавается любая функция y=ϕ(x;cₒ).юполученная из общего решения y=ϕ(x;c) при конкретном значение постоянной с=сₒ.2)если общее решение ДУ найдено в неявном виде,т.е. в виде уравнения Ф(x;y;с)=0,то такое решение называется общим интегралом ДУ.Уравнение Ф(x;y;сₒ)=0 в этом случае называется частным интегралом уравнения. Теорема(Существования и единственности решения задачи Коши) Если в уравнении y’=f(x;y) функция f(x;y) и ее частная производная f’ᵧ(x;y)непрерывны в некоторой области D,содержащей точку(xₒ;yₒ), то существует единое решение y=ϕ(x) этого уравнения, удовлетворяющее начальному уславию .Геометрический смысл: при выполнении ее условий существует единственная интегральная кривая ДУ,проходящая через точку(xₒ;yₒ)
Дефференциальные уравнения с разделяющимися переменными.
P(x)dx+Q(y)dy=0 в нем одно слагаемое зависит только от x,а другое –от y.Такие ДУ назыв. Уравнениями с разделенными переменными. Общий итеграл:∫P(x)dx+∫Q(y)dy=c. Замечание: 1)При проведение почленного деления ДУ на Q₁(y)*₂P(x) могут быть потеряны некоторые решения.Поэтому следует отдельно решить уравнение Q₁(y)*₂P(x)=0 и установить её решения ДУ,которые не могут быть получены из общего решения.2)Уравнение y’=f₁(x)*f₂(y) сводится к уравнению разделенными переменными.Для этого y’= 
и разделить переменные.3)Уравнение y’=f(ax+dy+c) a,d,c – число,замены ax+dy+c=u дифференцируем,получаем:
откуда следует 
интегрируя это уравнение и заменяя u на ax+by+c, получим общий интеграл исходного уравнения.
Однородные д.у первого порядка.
)M(x;y)dx+N(x;y)dy=0 y’=f(x;y) M(xy), N(xy) f(x;y) однород.функция в степени k f(tx;tq) tᵏf(x;y) проверим функц. На однородность,однор. Деф. Урав. 1-го порядка его решаенм вспомащью подстановки: y=Ux,y=u’x+u После преобразований получаем деф. Уравнения с разделяющ.переме. решая получаем интеграл yэ=u’x+u x=0(y≠0) U=Uкорн.ур. M(1;u)+N(1-u)u=0,f(tx;tu=f(x;y)=t⁰f(x;y)однород.деф.в 0- степени. U’x+u=2 
, 
y=ux 
yₒ=xln²(xc)приверим:u=0,y=0 0=2y+=0 y=0 –особое решение
Линейные д.у 1 порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида 
Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции. Доказано, что если функции a(x) и b(x) непрерывны на [a;b], то для любой начальной точки (x0, y0), x0∈ [a; b], задача Коши 
имеет единственное решение y = y(x) на [a;b].
18, Теорема об общем решении однородного д.у. Теорема 1 (о структуре общего решения линейного однородного ДУ). Если функции y 1(x), y 2(x), …, y n (x) образуют фундаментальную систему решений ДУ (2), то функция 
(3) является общим решением этого уравнения в области 
, 
, 
, …, 
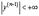; ci – произвольные постоянные,[ а, b ] – область непрерывности коэффициентов ai (x) уравнения (2), i = 1,2,..., n.
17. Линейные однородные д.у 2-го порядк. Свойства решений. Определитель Вронского. 14.5.4. Свойства решений линейного однородного дифференциального уравнения (25).
14.5.4.1. Теорема о линейности пространства частных решений линейного однородного дифференциального уравнения. Множество частных решений линейного однородного дифференциального уравнения образует линейное пространство.
Док-во. Требуется доказать, что множество частных решений линейного однородного дифференциального уравнения (25) (или, что тоже самое, (21)), т.е. не менее n раз дифференцируемых функций y (x) для которых Ln (y) = 0, является линейным пространством. Для этого достаточно доказать, что если функции y, y 1(x), y 2(x) - частные решения (25), то функции Cy, y 1(x) + y 2(x) - тоже частные решения (25). Действительно, пользуясь свойствами пункта 14.5.2. Линейный дифференциальный оператор и его свойства, получим
если Ln (y) = 0, то Ln (Cy) = CLn (y) = 0;
если Ln (y 1) = 0 и Ln (y 2) = 0, то Ln (y 1 + y 2) = Ln (y 1) + Ln (y 2) = 0.
Следствие. Если y 1(x), y 2(x), …, yn (x) - частные решения уравнения (25), то их линейная комбинация C 1 y 1(x) + C 2 y 2(x) + …+ Cnyn (x) - тоже частное решение этого уравнения. Теперь мы займемся определением размерности этого пространства и нахождением его базиса. Предварительно сформулируем и докажем несколько свойств определителя Вронского системы решений уравнения (25).
Теорема 14.5.4.2. Пусть y 1(x), y 2(x), …, yn (x) - частные решения линейного однородного дифференциального уравнения. Если определитель Вронского этой системы функций равен нулю в некоторой точке 
, то система функций y 1(x), y 2(x), …, yn (x) линейно зависима, и её определитель Вронского тождественно равен нулю на (a, b).
Док-во. Пусть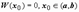 
. Тогда однородная система линейных алгебраических уравнений, для которой W (x 0) является определителем,
имеет нетривиальное решение относительно C 1, C 2, …, Cn. Рассмотрим линейную комбинацию функций y 1(x), y 2(x), …, yn (x) с этими коэффициентами C 1, C 2, …, Cn: y (x) = C 1 y 1(x) + C 2 y 2(x) + …+ Cn yn (x). Эта функция удовлетворяет уравнению (25) и, как следует из приведённой выше системы, имеет нулевые начальные условия в точке x 0, т.е. является решением задачи Коши
,
Этой же задаче Коши удовлетворяет и функция y (x) = 0, тождественно равная нулю на интервале (a, b). Вследствие единственности решения задачи Коши y (x) = C 1 y 1(x) + C 2 y 2(x) + …+ Cnyn (x) = 0 для 
. Таким образом, система функций y 1(x), y 2(x), …, yn (x) линейно зависима на (a, b), и по Теореме 14.5.4 о вронскиане линейно зависимой системы её определитель Вронского тождественно равен нулю на (a, b). Определителем Вронского (вронскианом) системы n - 1 раз дифференцируемых функций y 1(x), y 2(x), …, yn (x) называется определитель 
