Условие типового расчета.
Часть 1. Условие содержит матрицу оператора A: 
.
Часть 2. Задано уравнение кривой второго порядка:
3 x 2 + 2 xy + 3 y 2 – 6 
x – 2 y = –4.
Выполнение типового расчета.
Часть 1. Найдем собственные значения и собственные векторы симметрической матрицы:
Составим характеристическое уравнение (9.4)
| A – λE | = 
= 0
Раскрыв определитель и приведя подобные члены, получим уравнение третьей степени:
| λ 3 – 10 λ 2 – 13 λ + 22 = 0 | (9.16) |
В алгебре имеется теорема, утверждающая, что в приведенном уравнении произвольной степени, т.е. таком, в котором коэффициент при неизвестном в старшей степени равен единице, корни являются делителями свободного члена. Варианты настоящей работы составлены так, что собственные значения – числа целые, а, следовательно, они являются делителями числа 22.
Выписав эти делители ±1, ±2, ±11, ±22 – и подставляя их поочередно в уравнение (9.16) (для простоты расчетов начиная с меньших по абсолютной величине), найдем один из корней уравнения. В нашем случае λ = 1 – корень уравнения. Многочлен, стоящий в левой части уравнения (9.16) может быть разложен на множители:
λ 3 – 10 λ 2 – 13 λ + 22 = (λ – 1)(λ 2 + pλ + q)
Неизвестные коэффициенты p и q квадратного трехчлена могут быть найдены, например, делением многочлена третьей степени на двучлен (λ – 1). Деление многочлена на многочлен осуществляется по правилам, аналогичным правилам деления многозначного числа на многозначное. Роль цифр высшего и низшего разрядов играют члены, содержащие переменную в высшей и низшей степенях. Перед делением члены делимого и делителя располагаются в порядке убывания степеней переменной:
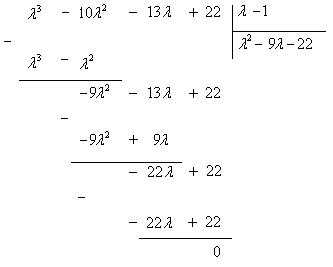
Опишем процесс деления подробно.
1. Делим первый член делимого λ 3 на первый член делителя λ, результат λ 2 есть первый член частного.
2. Умножаем полученный член на делитель λ – 1, результат λ 3 – λ 2 подписываем под делимым.
3. Вычитаем члены результата из соответствующих членов делимого; сносим остальные члены делимого, получаем – 9 λ 2 – 13 λ + 22.
4. Первый член остатка – 9 λ 2 делим на первый член делителя, результат – 9 λ есть второй член частного.
5. Умножаем полученный второй член частного на делитель, результат – 9 λ 2 + 9 λ подписываем под первым остатком.
6. Вычитаем члены этого результата из соответствующих членов первого остатка; сносим оставшийся член первого остатка; получаем второй остаток – 22 λ + 22.
7. Первый член второго остатка – 22 λ делим на первый член делимого; результат -22 есть третий член частного.
8. Умножаем, полученный третий член частного на делитель, результат – 22 λ + 22 подписываем под вторым остатком.
9. Вычитаем члены этого результата из второго остатка, получаем нуль. Деление закончено.
Таким образом, разложив на множители левую часть уравнения (9.16), получили (λ – 1)(λ 2 – 9 λ – 22) = 0. Отсюда находим собственные значения линейного оператора
λ 1 = 1, λ 2 = – 2, λ 3 = 11.
Для нахождения соответствующих им собственных векторов необходимо решить однородные системы (9.5).
При λ = 1
Записываем расширенную матрицу системы и ищем решение по методу Гаусса:
.
Ранг матрицы коэффициентов равен 2, следовательно имеем одно свободное неизвестное, в качестве которого примем x 3.
Тогда решение запишется:
или 
. При 
.
Так как собственный вектор определяется с точностью до числового множителя, свободное неизвестное принимаем таким, чтобы координаты вектора были взаимно простыми целыми числами.
Аналогично находим собственный вектор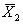 
, соответствующий собственному значению λ 2 = –2:
=>
.
Отсюда x 3 = 0. Следовательно, в качестве свободного неизвестного здесь нельзя брать x 3, так как оно фиксировано. Выбираем в качестве свободного неизвестного x 2, тогда решение запишется:
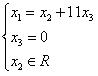или 
. При x 2 = 1: .
Контроль расчетов:
Убедимся в ортогональности собственных векторов X 1 и X 2:
= 1 · (–1) + (–1) · 1 + 2 · 1 = 0.
Аналогично убеждаемся: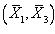 
= 0; 
= 0.
Система собственных векторов ортогональна.
Составим матрицу перехода T, столбцами которой являются найденные собственные векторы. Для окончательной проверки расчетов умножим матрицу A на T:
| (9.17) |
Каждый столбец полученной матрицы есть произведение матрицы A на соответствующий собственный вектор. Согласно определению собственного вектора это произведение должно быть равно произведению собственного числа на собственный вектор:
; 
; 
.
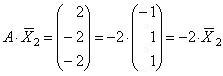Контроль подтвердил правильность расчетов.
Составленная матрица T является матрицей перехода к базису из собственных векторов. Матрица 
линейного оператора в базисе из собственных, векторов ищется по формуле (9.6). Найдем сначала матрицу T –1, являющуюся обратной матрицей T.
.
Контроль расчетов при нахождении обратной матрицы рекомендуем провести, перемножив матрицы T и T –1, так как, согласно определению, T · T –1 = E – единичная матрица.
Для нахождения A умножим T на матрицу A · T, найденную при контроле расчетов (9.17):
.
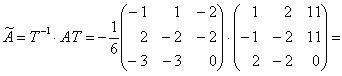
Результат расчетов согласуется с формулой (9.8).
Часть 2. Проведем исследование уравнения кривой второго порядка:
| 3 x 2 + 2 xy + 3 y 2 – 6 x – 2 y = –4
| (9.18) |
Для приведения уравнения к каноническому виду необходимо перейти к базису из нормированных собственных векторов ē 1, ē 2 матрицы квадратной формы (9.11):
.
Находим собственные значения матрицы A, как корни характеристического уравнения (9.12):
| A – λE | = 
= 0.
Раскрывая определитель и приводя подобные члены, приходим к уравнению λ 2 – 6 λ + 8 = 0, корни которого λ 1= 4, λ 2 = 2.
Координаты собственных векторов находятся из решения однородных уравнений (9.13).
При λ 1 = 4 
.
Откуда c 11 = c 21, c 21 є R. Полагая c 21 = 1, получим 
.
Аналогично находим второй собственный вектор:
λ 2 = 2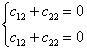 
.
Откуда c 12 = – c 22, c 22 є R. Полагая c 22 = 1, получим 
.
Убеждаемся, что найденные собственные векторы ортогональны между собой. Изобразим векторы 
и 
на плоскости в базисе векторов 
, 
(рис. 9.2).
Рис. 9.2 Собственные векторы в системе координат x, y
Поворот от вектора к вектору 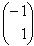совершается против часовой стрелки. Тем самым мы убеждаемся, что нумерация собственных векторов выбрана правильно, т.е. первый вектор , второй – 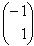. В противном случае, т.е. если бы указанный поворот совершался по часовой стрелке, нумерацию собственных векторов следовало бы поменять.
Для контроля расчетов составим матрицу T, столбцами которой являются найденные собственные векторы, и перемножим матрицы A и T:
.
Убеждаемся,
,
что подтверждает правильность расчетов.
Пронормируем найденные собственные векторы:
ē 1 = 
, ē 2 = .
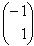Получили новый базис (ē 1, ē 2), получающийся поворотом старого на угол π / 4 против часовой стрелки. Старые координаты x, y в базисе , и новые x′, y′ в базисе ē 1, ē 2 связаны соотношениями (9.14):
 или 
| (9.19) |
Подставим (9.19) в уравнение кривой (6.10):
.
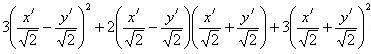
Раскрыв скобки и приведя подобные члены, получим:
4 x′ 2 + 2 y′ 2 – 8 x′ + 4 y′ + 4 = 0,
что согласуется с формулой (9.15): коэффициентами при x′ 2 и y′ 2 стоят собственные числа 4 и 2. Сокращая на 2 и выделяя полные квадраты, получим
2(x′ – 1)2 + (y′ + 1)2 = 1 или 
.
Следовательно, уравнение (9.18) является уравнением эллипса с полуосями и 1 и центром в точке (1,–1) новой системы координат.
Чтобы изобразить полученную кривую в исходной системе координат, удобно рассчитать координаты характерных точек кривой в этой системе координат. Для этого рисуем кривую в новой системе координат X′O′Y′ (рис. 9.3).
Рис. 9.3 Полученная кривая в системе координат x′, y′
Выписываем координаты характерных точек в системе X′O′Y′. В нашем случае это центр кривой Q и вершины эллипса ABCD. По формуле (9.19) находим координаты этих точек в исходной системе:
| Точка | Координаты (x′, y′) в системе X′ O′ Y′ | Координаты (x, y) в системе X O Y |
| Q | (1; –1) | ( ; 0)
|
| A | (1 + 1/ ; –1)
| ( + 1/2; 1/2)
|
| B | (1 –1/ ; –1)
| ( –1/2; –1/2)
|
| C | (1; 0) | (1/ ; –1/ )
|
| D | (1; –2) | (3/ ; –1/ )
|
Наносим рассматриваемые точки в старой системе координат XOY после чего несложно нарисовать изучаемую кривую в этой системе координат (рис. 9.4).
Рис. 9.4 Полученная кривая в исходной системе координат x, y
Замечание. Если заданная в условии задачи кривая оказывается гиперболой, необходимо изобразить ее асимптоты. Для этого уравнение асимптот записывают в новой системе координат x′, y′, затем из формул (9.19) выражают новые координаты x′, y′ через старые x, y и делают замену в уравнениях асимптот, записывая их тем самым в старой системе координат. После этого несложно нарисовать асимптоты на чертеже.
Оформление отчета
В отчете по первой задаче должно быть представлено характеристическое уравнение и его решение, решение однородных систем для нахождения собственных векторов. Полученные собственные векторы должны быть проверены на ортогональность, а также согласно определению собственного значения и собственного вектора. Далее должно быть показано преобразование матрицы A линейного оператора к базису из собственных векторов.
В ответе необходимо выписать собственные значения и соответствующие им собственные векторы:
.
По второй задаче должна быть представлена матрица квадратичной формы, нахождение ее собственных значений и собственных векторов. Собственные векторы необходимо проверить на ортогональность, а также согласно определению собственного значения и собственного вектора. Далее должно быть показано преобразование уравнения второго порядка при переходе к базису из ортонормированных собственных векторов и приведение его к каноническому виду. В работе должен быть сделан чертеж исходной системы координат, новой системы координат и построена кривая второго порядка.
В ответе по приведенному ниже образцу необходимо указать собственные значения и соответствующие им собственные векторы, формулы перехода от старых координат к новым, канонические уравнения кривой второго порядка, ее тип и основные числовые характеристики
λ 1 = 4, ē 1 = 
; λ 1 = 2, ē 2 = 
; 
.
В новых координатах x′, y′ кривая задается уравнением 
– каноническое уравнение эллипса с центром в точке (1;–1) и полуосями и 1.
