| Данное уравнение | y 2 – 16 x + 6 y – 23 = 0 |
| Уравнение кривой относительно ДПСК X'O'Y' (после параллельного переноса). | (y')2 = 16 x' |
| Название кривой | Парабола |
| Параметр | p = 8 |
| Эксцентриситет | ε = 1 |
| Связь между координатами точки (X,Y) и (X',Y') |  
|
| ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ | Координаты в ДПСК X'O'Y' | Координаты в ДПСК XOY |
| Вершина O' | (0, 0) | (–2, –3) |
| Фокус F | (4, 0) | (2, –3) |
| ЗАМЕЧАТЕЛЬНЫЕ ПРЯМЫЕ | Уравнение в ДПСК X'O'Y' | Уравнение в ДПСК XOY |
| Ось | y' = 0 | y = 3 |
| Директриса | x' = –4 | x' = –6 |
8. На рисунке 7.5 изображена парабола.
Рис. 7.5 Парабола
Задача 3.
1. По условию уравнение имеет вид:
2 x 2 + 3 y 2 – 12 x + 6 y + 21 = 0.
2. Так как A · B = 2 · 3 > 0, то уравнение эллиптического типа (см. 1, п. 1.1), следовательно, оно может определять либо эллипс, либо пустое множество (мнимый эллипс), либо точку.
3. Выделим полные квадраты:
2(x 2 – 6 x + 9) + 3(y 2 + 2 y + 1) – 18 – 3 +21 = 0;
2(x – 3)2 + 3(y + 1)2 = 0.
Точка с координатами (3, –1)
Замечание. Мы ограничились разбором решения только трех задач, однако это дает представление о выполнении работы в целом.
Порядок оформления работы
1. Все результаты каждой задачи должна быть сведены в таблицу, как это сделано в примерах. Таблица должна содержать каноническое уравнение и название кривой, основные числовые характеристики кривой (полуоси, расстояние от центра до фокусов, параметр, эксцентриситет), формулы, связывающие координаты точки относительно рассматриваемых ДПСК, координаты замечательных точек (центра, вершин, фокусов) и уравнения замечательных прямых (осей симметрии, директрис, асимптот) относительно всех рассматриваемых ДПСК.
2. Если рассматриваемая кривая – эллипс, то нужно сформулировать его основные замечательные свойства: фокальное, директориальное и оптическое, аналогично для гиперболы и параболы.
3. Решение задачи завершается аккуратно сделанным рисунком кривой в данной ДПСК.
В заключение отметим, что работа должна содержать не только ответы на вопросы, поставленная в задании, но и все вычисления, на основании которых сделаны выводы.
Исследование поверхностей второго порядка
Порядок оформления работы:
1. Все результаты каждой задачи должны быть сведены в таблицу (см. [1]). Таблица должна содержать:
- данное уравнение поверхности;
- каноническое уравнение и название поверхности;
- формулы, связывающие координаты точки относительно рассматриваемых декартовых прямоугольных систем координат (ДПСК);
- координаты начала новой ДПСК в данной ДПСК.
2. Должен быть сделан аккуратный рисунок поверхности в данной ДПСК.
Литература
1. Высшая математика. Раздел: Линейная алгебра и аналитическая геометрия. Учебное пособие по выполнению типовых расчетов. - М., МИСиС, 1990, № 687, стр. 88-100.
Исследование поверхностей второго порядка
Цель работы
Научиться определять тип поверхностей и научиться рисовать их.
Теоретическое введение
Алгебраической поверхностью второго порядка называется поверхность, уравнение которой в декартовой прямоугольной системе координат (ДПСК) можно представить в виде
| ax 2 + by 2 + cz 2 + dxy + exz + fyz + gx + hy + kz + l = 0; (a 2 + b 2 + c 2 + d 2 + e 2 + f 2 ≠ 0) | (1) |
Для каждой поверхности, определяемой уравнением (1), можно подобрать такую новую ДПСК (повернутую), что уравнение поверхности примет вид:
| Ax 2 + By 2 + Cz 2 + Dx + Ey + Fz + G = 0; (A 2 + B 2 + C 2 ≠ 0) | (2) |
В типовом расчете дается уравнение именно вида (2). Как и в случае кривых второго порядка, уравнение (2) можно еще более упростить, если перейти к некоторой (новой) ДПСК, которая получается из данной параллельным переносом осей. В результате мы получим 17 различных видов уравнений. Однако для нас интерес будут представлять только 9; остальные уравнения либо ничего не определяют (например, 
) либо определяют уже изученные нами геометрические объекты (например, 
определяет прямую – ось OZ).Эти 9 уравнений можно переписать в специальном виде, который называется каноническим, в таблице приведены канонические уравнения, а также названия и рисунки соответствующие им алгебраических поверхностей второго порядка.
Сделаем ряд кратких замечаний относительно этих поверхностей.
1. Эллипсоид
| (3) |
симметричен относительно координатных плоскостей, координатных осей и начала координат. Следовательно, он имеет три плоскости симметрии XOY, XOZ и YOZ, три оси симметрии: OX, OY и OZ и центр симметрии – точку O (0, 0, 0).
Эллипсоид можно получить вращением эллипса вокруг одной из его осей и последующим сжатием. Он представляет собой ограниченную овальную поверхность. Плоскость либо не пересекает эллипсоид, либо касается его в одной точке, либо пересекает его по эллипсу. Например, плоскость z = 0. Пересекает данный эллипсоид по эллипсу 
.
2.Однополостный гиперболоид
| (4) |
как и эллипсоид, симметричен относительно координатных плоскостей, координатных осей и начала координат. Его можно получить вращением гиперболы вокруг ее действительной оси и последующим сжатием. Эта поверхность имеет вид бесконечной трубы, “нанизанной” на ось OZ и бесконечно расширяющейся при удалении “вверх” или “вниз” от плоскости XOY. Если однополостный гиперболоид (4) пересекать плоскостями, параллельными координатным, то в сечении могут получаться эллипсы (если плоскости параллельны XOY) или гиперболы. При сечении другими плоскостями могут также получаться и параболы, и пары пересекающихся прямых, и пары параллельных прямых. Отсюда, в частности, следует, что однополостный гиперболоид состоит из прямых, которые называют образующими. Этот последний факт широко используется в строительстве, например, при сооружении радиобашен.
3. Двуполостный гиперболоид
| (5) |
тоже симметричен относительно координатных плоскостей, координатных осей и начала координат. Его можно получить вращением гиперсолы вокруг ее мнимой оси и последующим сжатием. Эта поверхность распадается на две бесконечные выпуклые чаши. Плоскость, параллельная плоскости XOY, или не пересекает двуполостный гиперболоид (5), или касается его в одной точке, или пересекает по эллипсу; плоскости, параллельные XOY и YOZ, пересекают его по гиперболам, при сечении другими плоскостями могут получаться и параболы.
4. Конус второго порядка
| (6) |
Поверхность, образованная прямыми (образующими), проходящими через данную точку (вершину) и пересекающими данную линию (направляющую), называется конической или конусом.
Легко проверить, что уравнение (6) действительно определяет коническую поверхность с вершиной в начале координат (в т. О (0,0,0)), а направляющей является, например, эллипс, который получается в сечении плоскостью z = c. Как и все предыдущие поверхности, конус (6) симметричен относительно координатных плоскостей, координатных осей и начала координат. Любая плоскость пересекает конус (как и однополостный гиперболоид): плоскость XOY имеет с ним одну общую точку – начало координат – вершина конуса; плоскости, параллельные XOY, пересекают конус по эллипсам; сечения конуса координатными плоскостями XOZ и YOZ – пары пересекающихся прямых – образующие конуса; а плоскости, параллельные XOZ и YOZ, дают в сечении гиперболы; другие плоскости могут давать в сечении также параболы и прямые (в случае касания). Следует иметь в виду, что любая кривая второго порядка, полученная при сечении конуса плоскостью, является его направляющей.
В заключение отметим еще, что конус второго порядка можно получить вращением прямой вокруг оси, которую она пересекает и последующим сжатием.
5. Эллиптический параболоид
| (7) |
в отличие от предыдущих поверхностей имеет только две плоскости симметрии: XOZ и YOZ и одну ось симметрии: OZ. Его можно получить вращением параболы вокруг его оси симметрии и последующим сжатием. Эллиптический параболоид (7) имеет форму “чашки”, стоящей на плоскости XOY (точнее она касается плоскости XOY в начале координат); плоскости, параллельные XOY и лежащие ниже нее, не пересекают эллиптический параболоид, а лежащие выше – дают в сечениях эллипсы. Плоскости XOZ и YОZ и им параллельные дают в сечениях параболы. При сечении эллиптического параболоида (7) остальными плоскостями ничего другого мы получать не будем: либо плоскость пересекает параболоид (7) по эллипсу, либо по параболе, либо плоскость имеет одну общую точку с параболоидом (точку касания), либо, наконец, плоскость вообще не пересекает параболоид (7).
Эллиптический параболоид вращения со времен Архимеда широко используется в технике, так как он обладает оптическим свойством параболы.
6. Гиперболический параболоид
| (8) |
как и эллиптический параболоид, имеет две плоскости симметрии (XOZ и YOZ) и одну ось симметрии (OZ). В отличие от рассмотренных выше поверхностей, он не есть результат вращения кривой. Он имеет форму седла. Гиперболический параболоид (8) пересекает плоскость ХОZ по параболе x 2 = 2 pz, ветви которой обращены вверх, а плоскость YOZ – по параболе – y 2 = 2 pz, ветви которой обращены вниз. Вся поверхность может быть получена параллельным перемещением – скольжением второй параболы по первой. Любая плоскость пересекает гиперболический параболоид, в сечении могут получаться параболы, гиперболы (но не эллипсы) и пары пересекающихся прямых. Например, при сечении гиперболического параболоида (8) плоскостью XOY получаются прямые: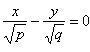 
и 
.
Последнее означает, что гиперболический параболоид состоит из прямых (как и однополостный гиперболоид), поэтому эта поверхность также находит применение в строительстве.
7. Эллиптический, гиперболический и параболический цилиндры
Поверхность, образованная параллельными прямыми (образующими), проходящими через все точки некоторой линии (направляющей), называется цилиндрической или цилиндром.
Например, цилиндром является поверхность, уравнение которой явно не содержит z, т.е. имеет вид F (x, y) = 0. В самом деле, эта поверхность состоит из прямых (образующих), параллельных оси OZ и проходящих через все точки кривой (направляющей), лежащей в плоскости XOY и уравнение которой имеет тот же вид, что и уравнение поверхности – F (x, y) = 0.
В частности уравнения
, 
, y 2 = 2 pz
определяют цилиндры, с соответствующими направляющими: эллипсом, гиперболой и параболой на плоскости XOY. Следует обратить внимание на то, что в нашем случае, хотя уравнения цилиндрических поверхностей и их направляющих имеют один и тот же вид, но смысл этих уравнений различный: в первом случае этому уравнению удовлетворяют координаты точек пространства (Х, Y, Z). во втором – координаты точек плоскости (Х, Y).Все сказанное относительно уравнений, которые явно не содержат z, естественно, справедливо и для уравнений, которые явно не содержат Y или Х, так уравнение F (x, z) = 0 определяет цилиндр с образующими, параллельными оси OY, а F (y, z) = 0 – цилиндр с образующими, параллельными оси ОX.
