Выполнение типового расчета

1. Найдем решение первой системы A ₁ · X = B ₁. Запишем систему в явном виде:

(2)

Запишем расширенную матрицу системы и будем делать элементарные преобразования со строками этой матрицы.
~ ~
На первом этапе преобразований в первом столбце, начиная со второй строки, получили, нули. Для этого использовали следующие элементарные преобразования: ко второй строке прибавили первую, к третьей и четвертой строкам прибавили первую, умноженную на (–3).
~ ~ ~
На втором этапе преобразований получили нули во втором столбце, начиная с третьей строки. Для этого к третьей строке прибавили вторую, умноженную на (–2), к четвертой cтроке прибавили вторую. Затем получили нули в третьем столбце четвертой строки, прибавив к четвертой строке третью. Для удобства дальнейших действий можно вынести из второй строки (–1) и из четвертой - (–2). Чтобы не изменился определитель матрицы A ₁, который нам нужно вычислить, вынесенный коэффициент ставим перед матрицей:
2· .
Определитель матрицы, преобразованной к треугольному виду, равен произведению чисел, стоящих на главной диагонали. Это можно показать, если разложить определитель по первому столбцу, получившийся после этого определитель вновь разложить по первому столбцу и т.д.:

Тогда с учетом стоящего перед матрицей коэффициента, | A ₁| = 6. Ранг матрицы A ₁ равен 4, ранг расширенной матрицы также равен четырем, ледовательно, система имеет единственное решение.

Рассмотрим два метода нахождения решения.
Метод 1. По полученной матрице выпишем преобразованную систему:

из которой последовательно определим значения неизвестных: - (3; –3; –1; 3).
Метод 2. С помощью элементарных преобразований полученную треугольную матрицу коэффициентов приведем к диагональному виду, для этого к третьей строке прибавим четвертую строку, умноженную на 2, ко второй и к первой строкам прибавим четвертую строку. Тем самым в четвертом столбце выше единицы четвертой строки получим нули. Продолжая аналогичные действия, приведем матрицу коэффициентов к диагональному виду:
~ ~ ~ ~
Теперь, разделив первую строку на 3, получаем единичную матрицу коэффициентов
~ 3· .
В выделенном столбце находятся решения исходной системы уравнений, так как полученная расширенная матрица соответствует следующей системе:
x ₁ = 3; ­ ­ ­ ­ ­ x ₂ = –3; ­ ­ ­ ­ ­ x ₃ = –1; ­ ­ ­ ­ ­ x ₄ = 3.
Полученное решение необходимо проверить, т.е. подставить в исходную систему (2).
Это удобнее всего сделать, введя матрицу решения X ₁ = ,
и умножая матрицу A ₁ на X ₁ справа. Если система решена верно, то результатом будет матрица B ₁.
Действительно A ₁ · X ₁ = 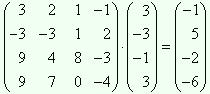= B ₁.

2. Запишем вторую систему A ₂ · X = B ₂ в явном виде:

По условию A ₁ = A ₂, т.е. вторая система отличается от первой только правыми частями, и главные определители у них равны, | A ₁| = | A ₂| = 6. Согласно теореме Крамера система имеет единственное решение, которое можно найти по формулам Крамера: . Вычислим вспомогательные определители.
Определитель |Δ₁| получается из главного определителя системы | A | заменой первого столбца на столбец правых частей:
; ­ ­ ­ ­ ­ .
Для вычисления этого определителя проведем предварительные преобразования. Преобразуем определитель |Δ₁| так, чтобы в его первой строке на первом месте осталась единица, а на всех остальных местах нули. Для этого ко второму столбцу прибавим первый столбец, умноженный на (–2); к третьему – первый столбец, умноженный на (–1); к четвертому – первый столбец. А затем вычислим полученный определитель разложением его по первой строке:

Получившийся определитель третьего порядка также преобразуем. Вынесем из второго столбца 4, а затем с помощью второго столбца организуем нули на первом и третьем месте первой строки. Для этого к первому столбцу прибавим второй, умноженный на (–13); к третьему столбцу прибавим второй, умноженный на 7. Затем разложим полученный определитель по первой строке и, наконец, вычислим полученный определитель второго порядка:

Следовательно,
Определитель |Δ₂| получается из главного определителя системы | A | заменой второго столбца на столбец правых частей:
| A | = |Δ₂| = .
Преобразуем определитель |Δ₂| так, чтобы в его первом столбце на первом месте осталось число 3, а на всех остальных местах – нули. Для этого ко второй строке прибавим первую строку; к третьей – первую строку, умноженную на (–3); к четвертому – также первую строку, умноженную на (–3). А затем вычислим полученный определитель разложением его по первому столбцу:
|Δ₂| =
Получившийся определитель третьего порядка преобразуем так, чтобы в третьем столбце на последнем месте стоял ноль. Для этого к третьей строке прибавим первую. Затем разложим полученный определитель по третьему столбцу и, наконец, вычислим полученный определитель второго порядка:

Следовательно, .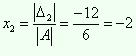
Определители |Δ₃| и |Δ₄| вычисляем аналогично, преобразуя и затем раскладывая по первому столбцу.


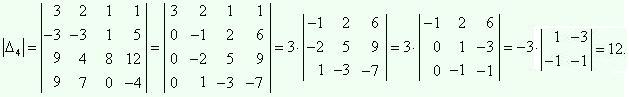
Откуда
Мы получили решение второй системы: или X ₂ = .
Сделаем проверку. A ₂· X ₂ = = B ₂.
Следовательно, система решена верно.

3. Проведем исследование третьей системы. Запишем систему A ₃ · X = B ₃ в явном виде:

(3)

Проведем необходимые элементарные преобразования над расширенной матрицей.

Определитель матрицы A ₃ равен нулю, ранг матрицы A ₃ равен 3 (одна нулевая строка в матрице ступенчатого вида), ранг расширенной матрицы равен 4 (нет нулевых строк). Так как ранги матрицы коэффициентов и расширенной матрицы не равны друг другу, то система (3) не имеет решения.

4. Рассмотрим четвертую систему. Запишем систему A ₄ · X = B ₄ в явном виде:

Проведем необходимые элементарные преобразования над расширенной матрицей:
.
Определитель матрицы A ₄ равен нулю, ранг матрицы A ₄ равен 2, ранг расширенной матрицы тоже равен 2. Так как ранги матриц равны, то система является совместной; ранг матрицы меньше числа неизвестных, следовательно, система является неопределенной. В преобразованной матрице жирным шрифтом выделен базисный минор. В качестве базисных неизвестных выберем x ₁ и x ₂ в, качестве свободных – x ₃, x ₄.
Перепишем полученную систему в виде

и введем x ₃ = C ₁ є R и x ₄ = C ₂ є R.
Окончательно получим x ₁ = 3 – C ₁ + C ₂; ­ ­ ­ ­ ­ x ₂ = 2 + C ₁ + 2 C ₂.
Решение неопределенной системы удобно записывать в векторном виде, выделяя фундаментальную систему решений однородной и частное решение неоднородной систем.

Для проверки и здесь удобно воспользоваться умножением матрицы A ₄ на матрицу X ₄, образованную из указанных выше трех векторов.

В полученной матрице первый столбец должен соответствовать вектору правых частей системы B ₄, а два других вектора должны быть нулевые, так как соответствующие решения являются решениями однородной системы уравнений.

Оформление отчета

В отчете по ТР должен быть представлены преобразования расширенных матриц каждой системы. Полученные решения должны быть проверены умножением матрицы коэффициентов на матрицу решений. В конце работы необходимо выписать общий ответ по следующему образцу:
1. Системы 1 и 2 – совместные, определенные.
| A ₁| = 6; ­ ­ ­ ­ ­ r (A ₁) = r (A ₁ | B ₁) = r (A ₁ | B ₂) = 4; ­ ­ ­ ­ ­ .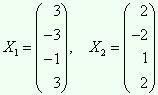
2. Система 3 – несовместная.
| A ₃| = 0; ­ ­ ­ ­ ­ r (A ₃) = 3; ­ ­ ­ ­ ­ r (A ₃ | B ₃) = 4.
3. Система 4 – совместная, неопределенная.
| A ₄| = 0; ­ ­ ­ ­ ­ r (A ₄) = r (A ₄ | B ₄) = 2; ­ ­ ­ ­ ­ .