Условие типового расчета
Уравнения кривых заданы таблицей из коэффициентов.
| № п/п | A | B | C | D | E |
| –36 | –50 | –72 | |||
| –16 | –23 | ||||
| –12 | |||||
| –4 |
Приведем решения первых трех задач, указанных в задании.
Задача 1.
1. По условию, уравнение имеет вид: 25 x 2 – 36 y 2 – 50 x – 72 y + 3589 = 0.
2. Так как AB = 25·(–36) < 0, то это уравнение гиперболического типа (см. 1, п. 1.2), следовательно, оно может определять или гиперболу, или пару пересекающихся прямых.
3. Выделим полные квадраты и приведем уравнение к каноническому виду:
25(x 2 – 2 x) – 36(y 2 + 2 y) + 3589 = 0;
25(x – 1)2 – 36(y + 1)2 = –3589 + 25 – 36;
25(x – 1)2 – 36(y + 1)2 = –3600;
 .
.
4. Перейдем к новой ДПСК X′O′Y′:
 ; ; 
| (12) |
Тогда наше уравнение примет вид

| (13) |
Теперь хорошо видно, что данное уравнение определяет гиперболу (см. III). Однако наша гипербола расположена относительно ДПСК X′O′Y′ не так, как изображено на рис. 7.2, а повернута на 90°, т.е. ее действительная ось – ось OY, а мнимая – OX.
5. Найдем основные числовые характеристики гиперболы.
Действительная полуось a = 10. Мнимая полуось b = 12.
Расстояние от центра до фокуса  .
.
Эксиентриситет гиперболы ε = c/d = 1.56 > 1.
6. Найдем координаты замечательных точек и уравнения замечательных прямых сначала в ДПСК X′O′Y′, затем, пользуясь формулами (7.12), в данной ДПСК XOY.
a) 
Следовательно, координаты центра гиперболы O' в данной ДПСК XOY будут (1,–1).
b) Уравнения осей симметрии. Как мы уже отмечали, наша гипербола имеет действительную ось – ось O'Y': x' = 0 и мнимую ось – ось O'X': y' = 0. С учетом (7.12) уравнение действительной оси x = 1, аналогично, уравнение мнимой оси: y = –1.
с) Вершины:
В системе X'O'Y'
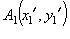 , где
, где  ;
;
 , где
, где  ;
;
отсюда, в системе XOY, A 1 (X 1, Y 1) = A 1(1; –11), A 2(X 2, Y 2) = A 2(1; 9).
d) Фокусы. В системе X'O'Y':


Отсюда в системе XOY: F 1(–1; –16,6); F 2(1; 14,6).
e) Директрисы.


L 1: y = –7,4; L 2: y = 5,4.
f) Асимптоты.
 .
.
x – 1,2 y – 2,2 = 0.
 .
.
x + 1,2 y + 0,2 = 0.
Γ 1: x – 1,2 y – 2,2 = 0; Γ 2: x + 1,2 y + 0,2 = 0.
7 Сводка полученных результатов
| Данное уравнение кривой | 25 x 2 – 36 y 2 – 50 x – 72 y + 3589 = 0 |
| Уравнение кривой относительно ДПСК X'O'Y' (после параллельного переноса) | 
|
| Название кривой | Гипербола |
| Полуоси | Действительная полуось a = 10 Мнимая полуось b = 12 |
| Расстояние от центра до фокуса | 
|
| Эксцентриситет | 
|
| Связь между координатами точки (X,Y) и (X',Y') |  ; ; 
|
| ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ | Координаты в ДПСК X'O'Y' | Координаты в ДПСК XOY |
| Центр O' | (0, 0) | (1, –1) |
| Вершины A 1 A 2 | (0; –10) (0; 10) | (1; –11) (1; 9) |
| Фокусы F 1 F 2 | (0; –15,6) (0; 15,6) | (1; –16,6) (1; 14,6) |
| ЗАМЕЧАТЕЛЬНЫЕ ПРЯМЫЕ | Уравнение в ДПСК X'O'Y' | Уравнение в ДПСК XOY |
| Оси Действительная Мнимая | x' = 0 y' = 0 | x = +1 y = –1 |
| Директрисы L 1 L 2 | y' = –6,4 y' = 6,4 | y = –7,4 y' = 5,4 |
| Асимптоты Γ 1 Γ 2 | x' = 1,2 y'x' = –1,2 y' | x – 1,2 y – 2,2 = 0 x + 1,2 y + 0,2 = 0 |
8. На рисунке 7.4 изображена гипербола.

Рис. 7.4 Гипербола
Задача 2.
1. По условию уравнение имеет вид
y 2 – 16 x + 6 y – 23 = 0.
2. Так как AB = 0 ·1 = 0, то это уравнение параболического типа (см. 1, п.2); далее, так как C ≠ 0 (см. 1, п. 2.1), то это уравнение определяет параболу.
3. Выделим полный квадрат:
(y 2 + 6 y + 9) = 16 x + 23 + 9; (y + 3)2 = 16(x + 2).
4. Перейдем к новой ДПСК X'O'Y'
 
| (14) |
тогда наше уравнение примет вид: (y')2 = 16 x'.
5. Найдем параметр: 2 p = 16, p = 8.
6. Найдем координаты замечательных точек и уравнения замечательных прямых:
а) Вершина  (См. (14)). O' (–2; –3).
(См. (14)). O' (–2; –3).
b) Уравнение оси: y' = 0, y + 3 = 0, т.е. y = –3.
c) Координаты фокуса F (p /2,0):
 F (2, –3).
F (2, –3).
d) Уравнение директрисы: z: X' = –p/2; X' = –4; X + 2 = –4 или X = –6.






