Для вывода дифференциального уравнения конвективного теплообмена в установившемся потоке жидкости (газа) выделяют элементарный параллелепипед с гранями dx, dy, dz (рис. 7.2) и составляют для него тепловой баланс, приняв физические параметры λ, с р и ρ постоянными. Скорости движения жидкости в направлении осей x, y и z, соответственно – wx, wy и wz. Температура жидкости t изменяется вдоль граней параллелепипеда. Теплоперенос в жидкости осуществляется путем конвекции и теплопроводности. Все подведенное к параллелепипеду тепло затрачивается только на изменение его энтальпии.
Количество тепла, которое вводится жидкостью путем конвекции по направлению оси х через грань dydz за время d τ,
.
За это же время через противоположную грань параллелепипеда путем конвекции жидкостью выводится количество тепла
,
или
.
Разность между количествами введенного и выведенного тепла в направлении оси х за время d τ составит:
.
Аналогично в направлении осей y и z
;
.
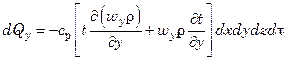Полная разность между количествами введенного и выведенного путем конвекции тепла в объеме параллелепипеда за время d τ
.
На основании уравнения неразрывности потока (1.34)
.
Тогда конвективная составляющая теплового потока
,
где 
– объем параллелепипеда.
Количество тепла, которое вводится в параллелепипед жидкостью путем теплопроводности за время d τ, в соответствии с уравнением (7.21)
.
Суммарное количество тепла, подведенное конвекцией и теплопроводностью
Это тепло dQ, согласно первому началу термодинамики, равно изменению энтальпии жидкости в объеме параллелепипеда
.
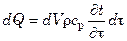Таким образом,
.
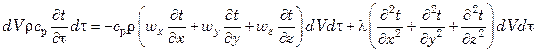В результате простейших преобразований последнего равенства, получим
,
либо
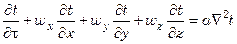, (7.66)
где 
– коэффициент температуропроводности.
Полученное уравнение (7.66) является дифференциальным уравнением конвективного теплообмена, или уравнением Фурье-Кирхгофа. Оно выражает в наиболее общем виде распределение температур в движущемся потоке жидкости (газа).
Для твердых тел wx = wy = wz = 0 и уравнение (7.66) превращается в дифференциальное уравнение теплопроводности (7.23).
При установившемся процессе теплообмена 
, тогда уравнение конвективного теплообмена для этого случая
. (7.67)
Ввиду сложности уравнения (7.66) для практического использования его подобно преобразовывают с учетом условий однозначности, т.е. представляют в виде функции от критериев подобия. Для этого, с целью более полного описания конвективного переноса тепла, дифференциальное уравнение Фурье-Кирхгофа дополняется граничными условиями, вытекающими из закона теплообмена на границе твердого тела и окружающей его среды.
Тепловое подобие
На практике процессы теплообмена осуществляются с помощью потоков разнообразных жидкостей и газов при различных режимах их движения в аппаратах различной геометрической формы и размеров. Однако условия подобия во всех случаях одинаковы и сводятся к подобию геометрических параметров, полей скоростей и температуры, а также физических констант. При этом должно соблюдаться подобие переноса тепла, как в пограничном слое, так и в ядре потока жидкости (газа).
Подобие переноса тепла в пограничном слое можно установить из краевых условий теплообмена на границе твердое тело – жидкость (газ), воспользовавшись зависимостью (7.64):
.
Применив тот же метод подобного преобразования уравнений, что и при выводе критериев гидродинамического подобия (см. раздел 1.3.6), разделим правую часть последнего равенства на левую:
.
Заменив 
на характерный (определяющий) геометрический размер 
, получим безразмерный комплекс величин, называемый критерием Нуссельта:
. (7.68)
Критерий Нуссельта характеризует теплоперенос через пограничный слой в форме соотношения количества тепла, передаваемого конвекцией, и теплопроводностью.
Аналогом критерия Нуссельта при нестационарном теплообмене между твердым телом и жидкостью или газом является критерий Био:
, (7.69)
где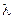 
– коэффициент теплопроводности твердого тела.
Условия подобия в ядре потока определяются из уравнения Фурье-Кирхгофа (7.66). Для одномерного движения потока жидкости его можно представить в виде
. (7.70)
Поделив члены левой части на правую часть, отбросив знаки математических операторов и заменив величины 
и 
на характерный геометрический размер и осредненную скорость 
соответственно, получим
;
.
Полученный комплекс 
обычно для удобства заменяют обратной величиной 
, которая выражает необходимое условие подобия неустановившихся процессов теплообмена. Этот безразмерный комплекс получил название критерия Фурье:
. (7.71)
Комплекс 
является мерой соотношения между теплом, переносимым конвекцией и теплопроводностью при конвективном теплообмене, и носит название критерия Пекле:
. (7.72)
Необходимым условием теплового подобия являются предшествующие ему гидродинамическое и геометрическое подобия. Гидродинамическое подобие определяется критериями гомохронности Но, Рейнольдса Re и Фруда Fr, а геометрическое – постоянством отношений основных геометрических размеров поверхности (стенки) к некоторому характерному размеру L. В качестве характерного линейного размера для трубных поверхностей, которые часто используются в качестве теплопередающих, принимают диаметр трубы L = d, иногда – длину трубы L = l, радиус кривизны изогнутой трубы L = R и т.д. В результате критериальное уравнение конвективного теплообмена выражается функцией вида
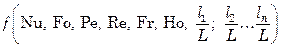, (7.73)
где 
– симплексы геометрического подобия.
Равенство критериев Нуссельта является следствием подобия геометрических и физических характеристик, а также подобия полей скоростей и температур. Поэтому Nu не является определяющим. В связи с этим обобщенную зависимость, описывающую кинетику переноса тепла в движущихся средах, представляют в виде
. (7.74)
Критерий Пекле обычно представляют в виде двух безразмерных комплексов
,
где 
– критерий Прандтля, характеризующий физические свойства теплоносителя (жидкости или газа).
По физическому смыслу критерий Pr определяет соотношение полей скоростей и температур в потоке. Для капельных жидкостей он зависит от температуры (с повышением температуры увеличивается), а его численные значения лежат в пределах 3 ÷ 300. Для газов критерий Прандтля не зависит ни от температуры, ни от давления, являясь постоянной величиной для газов одинаковой атомности (для одноатомных газов Pr = 0,67; для двухатомных Pr = 0,72; для трехатомных Pr = 0,8; для четырехатомных и более Pr = 1).
С введением критерия Прандтля уравнение (7.74) принимает вид:
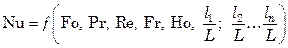. (7.75)
При установившихся тепловых процессах и одинаковой геометрической форме потоков из уравнения (7.75) исключаются критерии Fo и Ho, содержащие время, и геометрические симплексы, тогда
. (7.76)
При рассмотрении конкретных задач теплообмена уравнение (7.76) может быть видоизменено.
Так, при вынужденном движении, когда влияние сил тяжести на гидродинамику потока пренебрежительно мало, критерием Фруда можно пренебречь и критерий Нуссельта будет являться функцией лишь двух критериев:
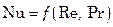. (7.77)
При свободном движении жидкости (в условиях естественной конвекции) из критериального уравнения исключают критерий Рейнольдса:
. (7.78)
Ввиду сложности определения скорости при естественной конвекции, входящей в критерий Фруда, последний заменяют производным критерием Архимеда, характеризующим естественную конвекцию, обусловленную разностью плотностей жидкости (газа) в различных точках потока:
,
где ρ и ρ0 – плотности холодной и нагретой жидкости (газа).
Поскольку в тепловых процессах разность плотностей в различных точках системы обусловливается разностью температур Δ t нагретой и холодной жидкости, комплекс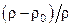 
в критерии Архимеда целесообразно выразить через произведение bΔ t (b – температурный коэффициент объемного расширения). Полученный новый критерий является критерием Грасгофа:
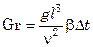. (7.79)
Таким образом, критерий Gr представляет собой определяющий критерий теплового подобия при естественной конвекции, когда движение жидкости целиком обусловлено самим процессом теплообмена, а уравнение конвективного теплообмена для этого случая
. (7.80)
Для газов при Pr ≈ 1 уравнение (7.79) превращается в функциональную зависимость критерия Нуссельта от критерия Грасгофа.
Помимо приведенных критериев теплового подобия в литературе часто встречаются производные критерии, составленные из указанных выше:
критерий Стантона 
, (7.81)
который отражает соотношение количества тепла, передаваемого конвекцией, и тепла, переносимого движущимся потоком;
критерий Релея 
; (7.82)
критерий Грэтца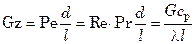 
, (7.83)
(G – массовый расход жидкости) характеризует конвективный теплоперенос при ламинарном режиме.
.
В соответствии с полученными критериальными уравнениями обрабатываются опытные данные по переносу тепла конвекцией и представляются в виде степенных уравнений. Например, уравнение (7.77) – в виде 
; уравнение (7.79) – в виде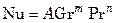 
и т.д.
При решении практических задач по найденному из соответствующего критериального уравнения значению критерия Нуссельта определяют коэффициент теплоотдачи:
.
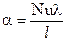Критериальные зависимости в виде степенных уравнений, как уже указывалось, решают чисто эмпирически и применимы они лишь в тех пределах изменения аргумента, в которых подтверждены опытом. Поэтому области их надежного применения ограничены пределами, указываемыми в каждом отдельном случае. Ограничения эти, в основном, связаны с характером и режимом движения потока теплоносителя, его геометрической формой и размерами, изменением агрегатного состояния.
