Гидродинамический и тепловой пограничные слои

Рисунок 7.16 – Изменение скорости в гидродинамическом пограничном слое

Как известно, в результате действия сил вязкости у твердой поверхности образуется тонкий слой заторможенной жидкости (гидродинамический пограничный слой), в пределах которого скорость изменяется от 0 до скорости невозмущенного потока w ₀ (рис. 7.16). Внутри пограничного слоя и , за пределами этого слоя и .

Толщину пограничного слоя можно представить как расстояние от поверхности, на котором скорость будет отличаться от скорости потока вдали от границы на определенную, заранее заданную малую величину :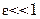

при .

Во внешнем потоке преобладают силы инерции, в пограничном слое силы инерции и вязкости соизмеримы. Тогда система дифференциальных уравнений, описывающих стационарное поле скоростей при омывании плоской пластины, бесконечной в направлении оси z, будет иметь вид:

; (7.135)

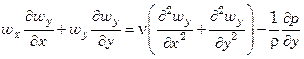, (7.136)

а уравнение сплошности

. (7.137)

Ввиду малой толщины пограничного слоя можно принять . Кроме того, если принять, что во внешнем потоке w ₀ = const, то из уравнения Бернулли следует, что во внешнем потоке давление не изменяется, т.е. .

Так как для пограничного слоя , а во внешнем потоке , то внутри пограничного слоя в рассматриваемом случае также равно нулю.

Для оценки порядка величин членов дифференциальных уравнений(7.135)–(7.137) выбраны масштабы предельной координаты l, порядок которой обозначен через o, и поперечной координаты у, порядок которой . Порядок величины w_x оценивается как w _o. Тогда

.

Согласно уравнению сплошности (7.137), порядок производных и одинаков, отсюда

.

Порядок величины w_y можно оценить как

.

Оценка отдельных членов инерционной (конвективной) и вязкостных частей уравнений движения в проекциях на ось х приводит к выражениям:

;

;

;

.

 

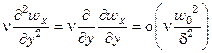Из этой оценки следует, что порядок отдельных слагаемых инерционной части одинаков и равен .

Отношение вязкостных членов дает:

.

Для пограничного слоя , отсюда .

Следовательно, последней производной можно пренебречь. Тогда уравнение движения в проекциях на ось х может быть записано в следующем виде:

. (7.138)

Порядок левой части этого уравнения равен , правой – , приравнивая их, получим

или , (7.139)

где – число Рейнольдса, характеризующее соотношения сил инерции и сил вязкости.

Если Re<<1, то , т.е. . В этом случае нет разделения потока на две области, все пространство жидкости у тела охвачено действием сил вязкости.

Если Re >>1, то , т.е. у поверхности тела образуется сравнительно тонкий слой подторможенной жидкости.

Таким образом, теория пограничного слоя приобретает характер метода упрощения математической формулировки краевой задачи и связанной с этим возможности решения.

Аналогичная оценка порядка величин, входящих в уравнение движения в проекциях на ось у, показывает, что члены этого уравнения малы и поэтому для пограничного слоя оно может быть опущено. Тогда для плоского безградиентного стационарного течения вязкой жидкости в пограничном слое у плоской поверхности

; (7.140)

. (7.141)

Внутри теплового пограничного слоя 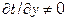, а на внешней границе и вне его и t = t ₀ (рис. 7.17).

Толщины гидродинамического (d) и теплового () пограничных слоев, как уже указывалось ранее, в общем случае не совпадают, что зависит от рода жидкости и некоторых параметров процесса течения и теплообмена. Можно предположить, что они одного порядка: k = 0(d). В связи с малой толщиной k теплового пограничного слоя можно пренебречь теплопроводностью вдоль него по сравнению с поперечным переносом теплоты, т.е. принять, что

Рисунок 7.17 – Изменение температуры в тепловом погтраничном слое

(,т.к. ).

Тогда уравнение энергии принимает вид

. (7.142)

Однако следует отметить, что система полученных дифференциальных уравнений (7.140)–(7.142) описывает теплообмен только в ламинарном пограничном слое. Турбулентное течение существенно отличается от ламинарного (см. рис. 7.10). Произведя некоторые преобразования и выдвинув дополнительные гипотезы, можно получить систему дифференциальных уравнений, описывающих в первом приближении осредненное турбулентное течение и теплообмен, но в достаточно строгой постановке этот вопрос до конца не разрешен.

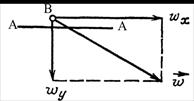Рисунок 7.18 – Мгновенное значение скорости в плоском турбулентном потоке

При рассмотрении качественной стороны явления переноса энергии в турбулентном потоке можно выделить условную контрольную поверхность А – А, расположенную параллельно плоскости X–Z (рис. 7.18).

В любой фиксированной точке В, расположенной вблизи поверхности А-А, в некоторый момент времени скорость турбулентного потока имеет компоненты w_x и w_y. Температура жидкости в этой точке равна t. За время в направлении оси у через единицу контрольной поверхности проходит масса жидкости (кг/м²), а относительно оси х – количество движения и соответственно энтальпия . В следующий момент времени компоненты скорости могут быть другими. Среднеинтегральное значения параметров потока могут быть определены на основе следующих свойств среднеинтегрального осреднения меняющихся во времени величин 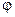и :

; ; ;

.

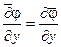Осредняя , получим

.

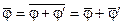Отсюда . Однако , что следует из уравнения .

Таким образом, среднеинтегральное значение плотности теплового потока q_у (Дж/м²·с), переносимого в направлении оси у за единицу времени через единицу контрольной поверхности, будет

. (7.143)

Величину можно представить в виде

(7.144)

Среднеинтегральное значение количества движения относительно оси х, переносимое в направлении оси у за единицу времени через единицу поверхности, можно получить аналогично:

. (7.145)

Итак, конвективный перенос тепла и импульса складывается из осредненного и пульсационного (турбулентного) переноса q _т и s _т.

;

.

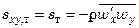В общем случае q _т и s _т не равны нулю; в определенных областях турбулентного потока, омывающего твердое тело, q _т и s _т могут принимать большие значения.

Рассмотрим течение около стенки на некотором удалении от нее, при этом осредненные значения скорости и температуры изменяются только в направлении оси у (рис. 7.19).

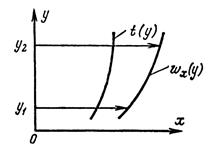Рисунок 7.19 – К выводу уравнений осредненного турбулентного переноса теплоты и количества движения

Предположим, что за счет пульсаций из слоя у ₁ в слой у ₂ переносится энтальпия с_pt (y ₁), где t (y ₁) – осредненное значение температуры при у = у ₁. Плоскости у ₁ и у ₂ параллельны плоскости xz. Разность энтальпий с_р [ t (y ₁) – t (y ₂)] равна переносимой теплоте на расстоянии . На длине пульсация не распадается, не диссипирует. Распад пульсационного движения при у = у ₂ приводит к передаче энтальпии слою у ₂ и пульсации температуры (так как фиксирована). Параметр называют длиной пути смешения, эта величина не является постоянной в турбулентном движении.

Разность можно представить следующим образом, используя разложение в ряд:

 

Тогда для пульсационного переноса теплоты можно записать:

. (7.147)

Аналогично для переноса количества движения

. (7.148)

Таким образом, величины q _ти s _т пропорциональны производным и . Учитывая это, последние уравнения могут быть записаны как определения в виде:

; (7.149)

 

, (7.150)

где и – коэффициенты турбулентного переноса теплоты и количества движения соответственно; , – кинематические коэффициенты переноса теплоты и количества движения.

Коэффициенты и не являются физическими параметрами среды, а зависят от параметров процесса.

Теплота и количество движения в направлении оси у переносятся также и молекулярным механизмом. В результате

; (7.151)

 

.

На стенке: у = 0, , , . Вдали от стенки: – и . Таким образом, при записи уравнений в осредненных значениях скорости и температуры следует учитывать и турбулентный (пульсационный) перенос теплоты и количества движения.

Для турбулентного пограничного слоя при принятых ранее ограничениях уравнения энергии (7.142), движения (7.140) и сплошности (7.141) могут быть записаны в следующем виде:

; (7.152)

; (7.153)

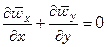. (7.154)

Полагают, что и зависят от тех же факторов (переменных), от которых зависят поля осредненных скорости и температуры. Для замыкания системы дифференциальных уравнений (7.152)–(7.154) необходимо добавить уравнения, характеризующие связь и с этими переменными.

Предложено много способов, позволяющих в первом приближении замкнуть эту систему дифференциальных уравнений. Ниже приводится один из наиболее простых.

Ранее было показано, что

, или .

Пульсационная скорость . Примем .

Тогда .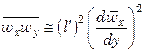

Введя коэффициент пропорциональности l, получим

. (7.155)

Величина l – длина пути смешения, пропорциональная ; иногда ее называют масштабом турбулентности.

При фиксированном значении касательное напряжение турбулентного трения s _т пропорционально l ².

Сравнивая уравнения (7.148) и (7.155), получим

. (7.156)

С учетом последнего выражения уравнение (7.147) может быть представлено в виде

. (7.157)

Последние выражения были предложены Л. Прандтлем. Согласно им в представленной области масштаб турбулентности (как и турбулентный перенос количества движения и теплоты) должен уменьшаться по мере приближения к стенке:

,

где .

Таким образом, в первом приближении задача замкнута, значения и (или и ) определены:

. (7.158)

Равенство (7.158) показывает, что существует аналогия между переносом количества движения и переносом теплоты, т.е. одни и те же объемы жидкости, участвуя в пульсационном движении, переносят одновременно количество движения и теплоту и не взаимодействуют на пути с окружающей средой. В действительности пульсационный перенос может сопровождаться теплообменом, может быть связан с диссипацией механической энергии из-за вязкости жидкости. Это заставляет вносить коррективы и вводить для описания переноса количества движения и теплоты различные значения l.

Несмотря на незавершенность описанной теории турбулентного пограничного слоя, она может быть использована для решения ряда практических задач.

Так, полученные выводы позволили решить задачу о профиле скоростей в пристенной области и ядре потока.

Для пристенной области профиль осредненной скорости является функцией следующих переменных:

,

где s ₀ – касательное напряжение на стенке; для тонкого слоя у стенки s ₀= s.

В случае касательное напряжение s

; .

Разделив переменные и проинтегрировав последнее равенство, получим

или .

Здесь 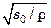– динамическая скорость.

Для турбулентной области

, ,

тогда .

Если ввести безразмерные переменные

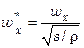и ,

то .

Проинтегрировав последнее уравнение, получим

. (7.159)

Следовательно, профиль скоростей в пристенной области носит логарифмический характер. Этот вывод был подтвержден экспериментально Никурадзе. Полный универсальный профиль скоростей описывается им следующей системой уравнений:

в ламинарном подслое (у^* <5) ;

в промежуточном слое (5< y^* <30) ; (7.160)

в турбулентном ядре (y^* >30) .

Выводы из описанной теории пограничного слоя позволили также связать теплоотдачу и гидравлическое сопротивление.

Согласно приведенным ранее соотношениям для касательного напряжения и теплового потока

;

, .

Либо

. (7.161)

Проинтегрировав это уравнение применительно к трубе в пределах от стенки до оси трубы, получим

, (7.162)

где w ₀, t ₀ – скорость и температура в ядре потока, t _cт – температура стенки;

; ,

тогда равенство (7.162) можно представить в виде

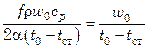. (7.163)

При турбулентном режиме профиль скорости в ядре потока плоский. С учетом подобия такой же профиль можно принять и для температурного потока. Отсюда следует, что w ₀ и t ₀ мало отличаются от среднерасходной скорости w и среднемассовой температуры t_m. Используя замену на , можно записать

.

Отсюда

. (7.164)

Полученное уравнение (7.164) позволяет рассчитать коэффициент теплоотдачи 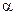через коэффициент гидравлического сопротивления f. Эта зависимость справедлива при .

 

Теплопередача

Одним из наиболее распространенных на практике видов сложного теплообмена является перенос тепла от одного теплоносителя к другому через разделяющую их стенку. В этом случае тепло от одного теплоносителя к стенке и от стенки к другому теплоносителю передается конвекцией (теплоотдачей), а через стенку – теплопроводностью. Такой способ переноса тепла получил название теплопередачи, а стенка – поверхности теплопередачи.