Основные понятия и определения
К тепловым процессам относят процессы, скорость которых определяется скоростью переноса энергии в форме теплоты – нагревание, охлаждение, конденсация и испарение.
Тепловые процессы часто сопутствуют другим технологическим процессам: химическим превращениям, разделению гомогенных смесей, сушке и т.д., которые сопровождаются подводом или отводом тепла.
Для тепловых процессов в химической промышленности характерны широкий диапазон изменения температуры (от нескольких тысяч градусов до близких к абсолютному нулю) и количеств передаваемой теплоты. Такой широкий диапазон требует применения различных способов передачи теплоты и материалов, которые наилучшим способом обеспечивают этот процесс.
Производства химической технологии, требующие больших затрат тепловой энергии, обычно комплексно связаны с тепловыми энергетическими установками. Рациональное расходование теплоты – важный экономический показатель эффективности работы аппаратуры и организации технологического процесса.
Перенос теплоты, происходящий между телами с различной температурой, носит название теплообмена. В соответствии со вторым законом термодинамики перенос тепла самопроизвольно происходит от тела с более высокой температурой к телу с меньшей температурой. Таким образом, причиной направленного теплопереноса является разность температур – температурный напор, который есть движущей силой переноса тепла. При выравнивании температур наступает равновесие.
Тела, участвующие в переносе тепла, называют теплоносителями.
Перенос теплоты может осуществляется различными способами. В зависимости от механизма различают три способа теплопереноса: теплопроводность, конвекция и излучение.
Теплопроводность – это перенос тепла при непосредственном соприкосновении тел с различной температурой, когда перенос энергии осуществляется микрочастицами за счет их «теплового» движения. В чистом виде теплопроводность наблюдается в твердых телах, а в жидкостях и газах – лишь в неподвижных средах. При этом в жидкостях и твердых телах (диэлектриках) перенос энергии осуществляется путем упругих волн, в газах – путем диффузии атомов или молекул, а в металлах, путем диффузии свободных электронов.
Конвективный перенос теплоты обусловлен массовым движением макрочастиц среды – теплота переносится движущейся средой. Такой способ теплопереноса возможен лишь в жидкостях и газах, при этом всегда сопровождается теплообменом между частицами посредством теплопроводности. В свою очередь, конвекция бывает свободной и вынужденной. Свободная конвекция происходит в результате разности плотностей жидкости или газа в различных точках занимаемого ими объема вследствие разных температур, вынужденная – когда перемещение частиц жидкости или газа происходит под действием внешних сил (с помощью насосов, компрессоров).
Тепловое излучение – это перенос энергии в форме электромагнитных колебаний, сопровождаемый переходом лучистой энергии в тепловую и наоборот. Этот вид переноса тепла имеет место между телами любого агрегатного состояния независимо от того, удалены ли они друг от друга или соприкасаются между собой.
В реальных условиях теплота чаще всего передается одновременно двумя или даже тремя способами. Однако обычно преимущественное значение имеет какой-нибудь один способ.
Наиболее распространенным случаем в практике является перенос тепла от одного теплоносителя к другому через разделяющую их стенку. Такой вид теплообмена называют теплопередачей. Процесс теплопередачи включает три стадии: 1) перенос теплоты средой, имеющей более высокую температуру, стенке; 2) перенос теплоты в стенке; 3) перенос теплоты от нагретой стенки к среде с более низкой температурой. Перенос теплоты в стенке происходит путем теплопроводности. Передача теплоты от теплоносителя к стенке и от нагретой стенки к более холодной среде называют теплоотдачей.
Особое место среди тепловых процессов занимают процессы, сопровождающиеся изменением агрегатного состояния теплоносителей (кипение, конденсация пара и т.д.).
В процессе переноса теплоты температура в общем случае изменяется в пространстве и во времени:
где t – температура; x, у, z – координаты; t – время. Пространство с различными температурами в отдельных его точках является температурным полем. Изменение температуры в данной точке пространства со временем характеризуют мгновенными температурами.
Процессы, в которых поля температур постоянны во времени, являются установившимися или стационарными. Они соответствуют непрерывно действующим аппаратам. Если же распределение температур в телах, участвующих в теплообмене, изменяется во времени, то процесс считается неустановившимся или нестационарным. Такие процессы протекают в аппаратах периодического действия.
Рисунок 7.1 – К определению температурного градиента
|
Геометрическое место точек, имеющих одинаковую температуру, образует изотермическую поверхность. Так как в одной и той же точке пространства одновременно не может быть двух различных температур, то изотермические поверхности разных температур друг с другом не пересекаются. Все они либо замыкаются на себя, либо кончаются на границах тела. Изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности. При этом наиболее резкое изменение происходит в направлении нормали n к изотермическим поверхностям (рис. 7.1).
Предел отношения изменения температуры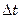 
к расстоянию между изотермами по нормали 
называют температурным градиентом 
:
Температурный градиент является вектором, направленным по нормали к изотермической поверхности. Его положительным направлением считается направление в сторону возрастания температуры. Значение температурного градиента, взятое с обратным знаком, называют падением температуры.
Количество тепла, проходящее через данную поверхность за время t, называют тепловым потоком Q [Дж]. Тепловой поток, проходящий в единицу времени через 1 м2 поверхности, носит название удельного теплового потока q 
.
Величина теплового потока зависит от теплофизических свойств теплоносителя. Непосредственное влияние на процесс переноса тепла оказывают температура, теплоемкость, температуропроводность, энтальпия, теплота фазового превращения.
Тепловые балансы
При теплообмене между теплоносителями происходит уменьшение энтальпии горячего теплоносителя и увеличение энтальпии холодного теплоносителя. Если расход горячего теплоносителя, его начальная и конечная энтальпии равны соответственно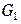 
, кг/с, 
и 
, а расход холодного теплоносителя, его начальная и конечная энтальпии – 
, кг/с, 
и 
, то уравнение теплового баланса в этом случае:
, (7.1)
где 
– тепло, теряемое в окружающую среду.
Таким образом тепло, отдаваемое горячим теплоносителем, частично передается холодному теплоносителю и частично расходуется на компенсацию потерь в окружающую среду.
В теплообменных аппаратах потери тепла в окружающую среду обычно невелики (не более 2–3 %) и ими можно пренебречь. Тогда уравнение теплового баланса примет вид:
, (7.2)
где 
– количество тепла, передаваемого от горячего теплоносителя к холодному (тепловая нагрузка аппарата, Вт).
Если теплообмен происходит без изменения агрегатного состояния теплоносителей, то их энтальпии равны произведению теплоемкости с на температуру t:
В последних выражениях 
– средние удельные теплоемкости горячего теплоносителя в интервале от 0 °C до температур 
; 
– средние удельные теплоемкости холодного теплоносителя в интервале температур от 0 °C до 
. Значения средних удельных теплоемкостей определяют из соотношений:
Приближенно средняя удельная теплоемкость в пределах от 0 °C до температуры t равна истинной удельной теплоемкости при температуре t /2, а средняя удельная теплоемкость в промежутке температур от t 1 до t 2 равна истинной удельной теплоемкости при температуре (t 1 + t 2)/2.
Если принять, что удельные теплоемкости не зависят от температуры, то
(7.3)
либо 
Произведение расхода G теплоносителя на его среднюю удельную теплоемкость c условно называют водяным эквивалентом W, который соответствует количеству воды, которое по своей тепловой емкости эквивалентно количеству тепла, необходимому для нагревания данного теплоносителя на 1 °С, при заданном его расходе. При использовании водяных эквивалентов горячего и холодного теплоносителей, соответственно W 1 и W 2, уравнение теплового баланса таково:
(7.4)
Если теплообмен сопровождается изменением агрегатного состояния теплоносителя (конденсация пара, испарение жидкости и др.) либо в процессе теплообмена протекают химические реакции, сопровождающиеся выделением или поглощением тепла, то в тепловых балансах необходимо учесть тепло, выделяющееся или поглощающееся в результате химических превращений.
Так, при использовании в качестве горячего теплоносителя пара процесс теплообмена сопровождается его конденсацией. Если пар насыщенный, то количество выделяющегося тепла при этом равно:
,
а тепловой баланс имеет вид:
. (7.5)
Здесь 
– энтальпия греющего пара, а 
– температура образовавшегося конденсата.
При температуре, конденсата равной температуре насыщения пара (
)
(r – удельная теплота конденсации).
Следовательно,
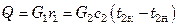. (7.6)
В более общем случае греющий пар может быть перегрет до температуры 
, а образовавшийся конденсат переохлажден до температуры 
.
Тогда общее количество выделившегося тепла будет включать три составляющих:
1) количество тепла, выделившееся при охлаждении пара до температуры насыщения 
:
,
где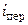 
– энтальпия перегретого пара;
2) количество тепла, выделившееся при конденсации насыщенного пара:
;
3) количество тепла, выделившееся при переохлаждении конденсата:
.
В итоге тепловой баланс в этом общем случае:
либо 
. (7.7)
При испарении холодного теплоносителя тепло расходуется на его подогрев до температуры насыщения в количестве 
и на парообразование 
(
– удельная теплота парообразования холодного теплоносителя). Тепловой баланс:
(7.8)
Если в качестве горячего теплоносителя при испарении холодного используется пар, то тепловой баланс выражается в виде равенства
, (7.9)
а при теплообмене между конденсирующимся паром (без переохлаждения конденсата) и кипящей жидкостью:
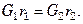(7.10)
Возможны и другие сочетания, выражающие баланс тепловых потоков. Однако, следует отметить, что во всех случаях, когда необходимо учитывать потери тепла в окружающую среду, к правой части равенств добавляют Q пот.
Пользуясь приведенными выше выражениями тепловых балансов и подобными им зависимостями, можно при прочих известных величинах рассчитать неизвестные потоки теплоносителей, одну из температур или тепловой поток Q.
Теплопроводность
Уравнение Фурье. Коэффициент теплопроводности
Теплопроводностью называют процесс переноса тепла, который целиком обусловлен обменом энергией между микрочастицами тела (среды), непосредственно соприкасающимися друг с другом.
В практических условиях, как уже указывалось, теплопроводность в наиболее чистом виде наблюдается в твердых телах. В жидкостях и газах возможность чистой теплопроводности практически исключается, так как в этом случае перенос теплоты осуществляется не только микрочастицами, но и макрочастицами среды (которые по размерам во много раз превосходят длины свободного пробега микрочастиц или амплитуду их колебаний), организующими перемещение жидкостей и газов.
В основе теории теплопроводности лежит закон Фурье, связывающий количество переносимой внутри тела теплоты с существующим температурным полем. Согласно этому закону количество тепла 
, переданное посредством теплопроводности, пропорционально падению температуры по нормали 
, времени 
и площади сечения 
, перпендикулярного направлению распространения тепла:
(7.11)
либо 
.
Величины и имеют тот или иной знак в зависимости от принятого направления нормали. Если за положительное направление принято направление теплового потока в сторону убывающих температур, то имеет отрицательное значение, так как направления теплового потока и градиента температур не совпадают. Тогда
(7.12)
или 
.
Коэффициент пропорциональности l в уравнениях (7.11) и (7.12) является коэффициентом теплопроводности (см. подразд. 7.3) и показывает, какое количество теплоты передается в единицу времени через единицу поверхности при падении температуры в 1 °С на единицу длины:
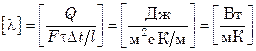
(l – линейный размер, м).
Значение коэффициентов теплопроводности зависит от структуры, удельного объема, влажности, давления и температуры. Численные значения l определяются опытным путем. Для наиболее распространенных веществ эти значения приводятся в справочной литературе. При выборе l из справочных таблиц следует учитывать соответствие физических свойств вещества – структуры, влажности, температуры и т.д. – и при необходимости вводить поправки.
Коэффициент теплопроводности твердых тел является функцией температуры:
, (7.13)
где 
– коэффициент теплопроводности при 0 °С; 
– постоянная для данного вещества; для большинства металлов < 0, т.е. l уменьшается с увеличением температуры, для большинства неметаллов (керамика, например) > 0, т.е. l увеличивается с повышением температуры.
В случае твердых пористых тел с порами, заполненными воздухом, коэффициент теплопроводности
, (7.14)
где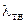 
– теплопроводность твердой фазы; 
– порозность тела.
Зависимость коэффициента теплопроводности газов от температуры может быть представлена уравнением Сатерленда:
, (7.15)
где ср и 
– удельные теплоемкости газа, соответственно при температурах Т и Т 0; С – постоянная для данного газа. Значения С для некоторых газов приведены в таблице 7.1.
Таблица 7.1 – Значения коэффициента С в уравнении (7.15)
| Газ | С, К | Температурные границы дляС, ºК |
| Азот | 288–373 | |
| Аммиак | 288–457 | |
| Водород | 71,7 | 253–573 |
| Воздух | 273–573 | |
| Двуокись серы | 288–373 | |
| Двуокись углерода | 253–573 | |
| Кислород | 288–463 | |
| Метан | 288–373 | |
| Окись углерода | 289–373 |
Коэффициенты теплопроводности жидкостей, как указано в подразделе 7.3, как правило, с увеличением температуры уменьшаются (исключение составляют вода и глицерин), изменение давления на величину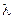 
практически не влияет. Приближенно коэффициент теплопроводности жидкостей можно рассчитать, пользуясь эмпирической формулой Вебера:
. (7.16)
В этой формуле 
и 
– плотность и удельная теплоемкость жидкости, соответственно; М – молярная масса; r – удельная теплота парообразования; 
– абсолютная температура кипения.
