Другие концепции интеллекта 9 страница

1. Зрительное прослеживание предметов и перманентность объекта.

2. Использование средств для повторения желаемых эффек­тов.

3. Голосовое подражание.

4. Жестовая имитация.

5. Причинность действия.

6. Пространственные связи предмета.

7. Схемы связей между предметами.

Для каждой их областей поведения подобрано от 7 до 14 заданий, ответы в которых оцениваются по шкале из 6 уровней. Авторы разработали способ построения профиля по уровню оценок в разных областях поведения. Был при-

менен показатель Н, предложенный Левингер, так как обычный коэффициент внутренней согласованности зада­ний не пригоден для порядковых шкал. При апробации ме­тодики авторы нашли высокие корреляции (0,84 — 0,96) результатов по семи шкалам с возрастом испытуемых (нор­мальных детей). В то же время у детей с задержкой развития корреляции оказались ниже, что нельзя считать неожидан­ным, так как здесь основное влияние оказывает не возраст, а степень умственной отсталости. Были вычислены также корреляции этого теста с упоминавшимися ранее порядко­выми шкалами Бейли. По данным Ренсен, эти корреляции оказались довольно высокими.

В целом на основе полученных результатов можно пола­гать, что высокие корреляции между показателями в раз­ных областях поведения ребенка объясняются наличием общего фактора — сенсомоторным развитием.

В другом исследовании Вервей (1994) использовал зада­чи на транзитивность числа, общего количества вещества и длины (если АВ и ВС, то АС) и применил к полученным эмпирическим данным несколько различных моделей и по­рядковую шкалу. Наиболее адекватной оказалась модель Моккена (1971). Кроме того, исследовав корреляции пол­ученной порядковой шкалы с результатами, полученными в тестах на арифметические операции и чтение, автор на­шел их достаточно высокими. Транзитивность может рас­сматриваться как пример упорядоченно развивающегося поведения, который хорошо описывается порядковой шка­лой.

Еще одно исследование, проведенное Бругманом (1994), строилось на основе концепции Колберга об уровнях мо­рального развития. Автор оценивал ответы финансовых экспертов (бухгалтеров) в предложенной им для решения проблеме, нередко встречающейся в практической работе. Проблема могла выглядеть, например, таким образом: «Не­кая компания находится в трудном положении, однако еще есть возможность поправить дела, если прибегнуть к ради­кальным нововведениям. Помещения компании располо­жены на участке земли, который можно очень выгодно продать. Представьте себе, что владелец (директор) компа­нии предлагает финансовым экспертам распустить компа­нию и уволить 300 служащих.» Ответы оценивались

 

определённым числом баллов, так что высший балл соот­ветствовал высшему уровню морального развития по шкале Колберга. Полученные результаты оказались не простыми для интерпретации. Например, имела место их корреляция с возрастом участников исследования. Бухгалтеры в возра­сте старше 46 лет получили оценки, указывающие на более низкий уровень морального развития, по сравнению с более младшими коллегами. Бухгалтеры, вместе работающие в фирмах с численностью служащих менее 10 человек, пол­учили более высокие оценки по сравнению с теми, кто ра­ботает в фирмах с большей численностью персонала. Порядковые шкалы и классическая теория тестов. Большинство интеллектуальных и личностных тестов созданы на основе классической теории тестов. Порядковые шкалы не полностью соответствуют канонам этой теории. Прежде всего в порядковых шкалах не предполагается фик­сированная единица измерения, как это делается при изме­рении согласно классической теории тестов. Имеются и некоторые другие отличия. Значение суммарной оценки в тестах классического типа определяется путем ее соотнесе­ния с нормами, полученными на репрезентативной выбор­ке. В порядковых шкалах значение результатов как бы содержится в самой оценке, поскольку она указывает на достигнутый уровень развития. В свою очередь, чтобы оце­нить его, надо обратиться ко всему ряду установленных уровней развития. В классическом тесте имеется множество способов получить суммарную оценку, скажем, 10 баллов, если тест состоит из 20 заданий, т.е. реальная комбинация правильных и ошибочных ответов в заданиях может быть самой разной. В отличие от этого в порядковой шкале способ набрать ту или иную сумму баллов однозначен. Примером может служить шкала Гуттмена. Так, чтобы получить оценку 4 в тесте, содержащем 8 заданий, необходимо пока­зать такие результаты: 11110000, и никакая другая комби­нация результатов невозможна. Для порядковых шкал коэффициенты общей внутренней согласованности (KR-20, KR-21, коэффициент «альфа» по Кронбаху) не пригод­ны, так как сами уровни и их последовательность носят упорядоченный характер. Здесь должны применяться дру­гие коэффициенты, например коэффициент Н, по Левин-гер. Возникают также некоторые вопросы и относительно валидности. Как мы уже отмечали, между порядковыми

шкалами и результатами тестов другого типа имеются кор­реляции. Следовательно, можно было бы получить сведе­ния о конструктной валидности. Однако в порядковых шкалах предполагается наличие специфической внутрен­ней структуры. Таким образом, если последовательность заданий в порядковой шкале подтверждается со стороны эмпирических данных, то это служит подтверждением кон­структной валидности шкалы, а следовательно, и психоло­гических характеристик.

Подведем некоторые итоги. Как показано в этом разде­ле, проблемы практического плана побудили психологов к разработке особого рода тестов, пригодных для обследова­ния развития маленьких детей. Эти методы получили на-звание «тестов развития», несмотря на то, что они создавались вне непосредственной связи с теориями психи­ческого развития. Для оценки и измерения тех сторон раз­вития ребенка, где присутствует достаточно постоянная и явная последовательность, были разработаны порядковые шкалы. Статистический аппарат, используемый в тестах классического типа, далеко не во всех отношениях приме­ним к результатам, полученным в порядковых шкалах. Не­смотря на то, что порядковые шкалы как с теоретической, так и с чисто технической точки зрения (в плане измерения) можно считать более прогрессивными, классические «тесты развития» не исчезнут, в силу их очевидного важного зна­чения для выявления детей с задержкой умственного раз­вития, а также большей простоты и ясности для диагностов. Следующим шагом в анализе и диагностике процесса раз­вития является создание математических моделей, описы­вающих феномены развития. Ниже мы приведем два примера такого рода.

6.4. Оценка развития:

математическое моделирование

феноменов психического развития

В отличие от психологии личности (если ненадолго за­быть о факторном анализе и классических работах в русле теории личностных черт, принадлежащих патриархам пси­хологии Айзенку и Кеттелу), психология развития распо­лагает возможностями математического моделирования некоторых феноменов психического развития. Обсуждают­ся два таких феномена. Тот и другой моделируются с по-

 

мощью нелинейных динамических моделей, которые не­давно привлекли к себе большое внимание. Эти модели отличаются от классических подходов дифференциальной психологии и экспериментальной психологии, в течение долгого времени преобладавших в психологии. Для них тре­буются лонгитюдные данные, получаемые в результате большого числа регулярных измерений. Модель сконстру­ирована таким образом, что включает в себя некоторый центральный элемент процесса изменения, происходящего с течением времени. Сбор данных ведется постепенно, и их порядок не рассматривается как «ошибочный» с той легко­стью, как это делается в классической теории тестов. Зна­чение переменной, отражающей развитие, в момент времени Т является функцией всех предшествующих зна­чений в Т-1, Т-2, Т-3,... Т-n. Влияние этих моделей на диагностику пока еще ограничено, поскольку там, по-ви­димому, все еще сохраняется ориентация в основном на результаты развития (как более стабильные образования), а не на процессы развития.

Процесс смены стадий (переход с одной стадии на следующую).

В работах Ван дер Мааса (1992,1993) и Моленаара (1992) некоторые характеристики математической теории катаст­роф были использованы для описания процесса перехода с дооперациональной стадии интеллектуального развития по Пиаже на стадию конкретных операций. С этой целью они разработали компьютеризованную версию из нескольких параллельных серий задач на разные виды понятия сохра­нения. Один и тот же испытуемый мог проходить тестиро­вание несколько раз.

Статистическая теория катастроф входит как составная часть в теорию нелинейных систем. Согласно этой теории, зависимые переменные связаны с независимыми и регули­руемыми переменными. В этой части она не отличается от принятых методик, подобных, например, линейной регрес­сии, которая так широко используется в психодиагностике и в психологии вообще. Преимущество теории катастроф связано с возможностью описать процессы, не носящие не­прерывного характера, иначе говоря, описать ситуации «разрыва», которые и называют «катастрофами» (Van der Maas, 1993). Форма катастроф зависит от переменных, уп-

равляющих процессом перехода с одной стадии на другую. Изменение может принимать многообразные формы. Воз­можно простое линейное возрастание, также как и рост по экспоненте, например, рост словарного запаса у детей. Классические кривые научения могут служить иллюстра­цией быстрого роста на начальном этапе, а затем постепен­ного асимптотического нарастания в течение продолжительного времени. Но рост также может не быть непрерывным. Переход с одной стадии на другую и рассмат­ривается авторами исследования как пример прерывности процесса. Такого рода переходы (смены стадий) зависят от изменений, происходящих в зависимой и контрольной пе­ременных. Авторы исследования искали модели, которые могли бы описывать резкие изменения и переходы. Одним из примеров такого изменения может служить переход воды в парообразное состояние.

Теория катастроф может быть использована в различных научных дисциплинах для решения разных проблем. Зада­ча этой теории — выявить и описать изменения, происхо­дящие в разного рода явлениях. Ван дер Маас использовал эту теорию для описания перехода между двумя стадиями когнитивного развития. В теории приводятся критерии, ко­торым должны удовлетворять эмпирические данные, чтобы указать на наличие катастрофы. Переход с одной стадии когнитивного развития на другую рассматривается как ка­тастрофа. Эта модель применяется также и для описания «реальных» катастроф. Например, с помощью таких моде­лей были описаны тюремные бунты в Англии. При этом возникло впечатление, что при определенных обстоятель­ствах даже небольшие изменения (например, простая ссо­ра) могут в результате привести к мощному бунту. Не исключено, что даже историк, изучающий штурм Бастилии в начале Великой французской революции, мог бы извлечь пользу из анализа, основанного на теории катастроф.

Ван дер Маас (1993, р. 11—24) вывел из этой теории 8 критериев. Если процессы перехода с одной стадии на дру­гую обнаруживают признаки соответствия этим критери­ям, то тогда такой переход можно описать как катастрофу. В рамках математической теории характеристики катаст­рофы имеют точное значение и способ описания. Связывая эти характеристики с явлениями развития, вероятно, мож-

 

но углубить наше понимание феноменов развития. Как уже говорилось, смену стадий можно рассматривать как пример катастрофы, если эмпирические данные обнаруживают следующие характеристики:

1. Резкий скачок, т.е. значительные изменения за короткий
период времени.

2. Много- или двумерность ответов, т.е. распределение от­ветов соответствует не кривой нормального распределе­ния, а кривой с двумя подъемами в связи с резким пере­ходом от неправильных ответов к правильным.

3. Возросшее расхождение ответов, т.е. множество колеба­ний между правильными и неправильными ответами, это период неопределенности или период экспериментирова­ния, когда можно наблюдать разные формы поведения.

4. Отступление от линейной зависимости ответов, здесь недействительно предположение, лежащее в основе мно­гих других моделей, что показатели поведения увеличи­ваются медленно и монотонно (многие шкалы развития опираются в качестве предпосылки на положение о моно­тонном возрастании той или иной функции в течение определенного периода развития!).

5. Задержка восстановления после некоторого нарушения (обычно человек восстанавливает свое состояние после некоторого нарушения, т.е. он возвращается на первона­чально занимаемую стадию, но в случае «катастрофы», когда нарушение носит гораздо более тяжелый характер, он, по-видимому, не восстанавливает исходный статус).

6. Недоступность (соответствует бимодальности, посколь­ку принадлежность одному типу распределения означает невозможность легкого перехода к другому типу распре­деления.

7. Хйстерезис' (этот феномен возникает тогда, когда одному и тому же значению независимой переменной соответст­вует несколько значений зависимой переменной). Хйсте­резис присутствует в области независимой переменной (а не в специфическом значении или точке, как это имеет место в Гуттмановской шкале) и в этой области (интерва­ле) значение независимой переменной (например, пока­затель понимания принципа сохранения) может быть вы­соким или низким). Представим себе, что пластилиновый

* Хйстерезис (от греч. hysteresis) — отставание, запаздывание (прим. пе-рев.).

шарик раскатывается в колбаску и становится все тоньше и длиннее, при этом ребенок начинает утверждать, что «пластилина все меньше и меньше». Представим теперь, что производится обратное преобразование: длинная, тонкая колбаска постепенно превращается в шарик. Ребе­нок меняет свой ответ, начиная утверждать, что «пласти­лина все больше и больше», но делает он это не обязатель­но в тот же самый момент, а следовательно, при другом значении независимой переменной, чем в первом случае. Таким образом, имеет место не локальная точка, а некая область или интервал значений независимой переменной, в котором происходит изменение, переход, смена стадий, перелом и т.д. 8. Расхождение (дивергенция) ответов (возможен как мед­ленный, так и резкий, быстрый переход, но в случае ка­тастрофического типа изменений можно ожидать дейст­вительно существенного отклонения ответов). Эти восемь характеристик взаимозависимы. Необходи­мо, чтобы'эти характеристики отчетливо присутствовали в результатах тестов на сохранение, в противном случае пе­реход с дооперациональной стадии на стадию конкретных операций нельзя уподобить изменениям по типу катастро­фы. Ван дер Маас попытался найти эмпирические подтвер­ждения, обследовав четыре группы учеников, отличавшихся по достигнутым уровням конкретных опера­ций. Результаты показали, что те, кто действительно достиг уровня конкретных операций, давали правильные ответы и применяли адекватные стратегии решения; те, кто еще не достиг уровня конкретных операций, давали неправильные ответы и демонстрировали ошибочные стратегии. Две дру­гие группы учеников занимали промежуточное положение. Ван дер Маас нашел подтверждение для некоторых, но не всех критериев. Он обнаружил бимодальное распределение ответов и возросший разброс в ответах детей. В то же время учащиеся, находившиеся на переходных стадиях, демонст­рировали противоречивые и плохо согласующиеся между собой результаты. Кроме того, переход отличался не ров­ным и плавным течением, а, напротив, наличием резких скачков. Причем не все такие скачки можно было считать «броском вперед», так как более чем 20% учащихся затем вновь возвращались на дооперациональную стадию. Это, однако, нельзя считать трудностью, связанной с теорией

 

катастроф или с концепцией стадий Пиаже, поскольку пе­риод колебаний вполне возможен. Противники такого под­хода расценили приведенные выше факты как признак отсутствия инвариантности; в таком случае необходимо признать, что перед теорией Пиаже встают трудные вопро­сы. Возникает вопрос о том, в чем заключается подлинный регресс.

Ван дер Маас (1993) считает, что он получил подтверж­дение существования стадий и перехода между ними. Его данные отвечают по крайней мере некоторым их критериев, вытекающих из теории катастроф.

Модель роста (развития).

Ван Геерт (1991) разработал модель динамической сис­темы для когнитивного развития при наличии ограничи­тельных условий. Интуитивно представляется весьма заманчивым рассмотреть процесс развития с точки зрения динамической системы. Это предполагает, что некий объ­ект может развиваться, но для его развития существуют определенные пределы, ограничения. Одновременно с про­цессом развития включаются некие механизмы сдержива­ния дальнейшего хода этого процесса. Ван Геерт предложил логистическую модель развития, в которой присутствует механизм отсроченной обратной связи. Данная модель бы­ла заимствована им из популяционной биологии.

Эта формула описывает то, как некоторый уровень раз­вития (L), достигаемый в момент времени t+1, представляет собой результат предшествующего уровня развития (в мо­мент времени t). Здесь также присутствуют два дополни­тельных параметра: r и К, где г обозначает темп развития, а К — развивающуюся способность. Реализованную спо­собность можно представить как отношение между числен­ностью популяции в настоящее время и плотностью населения, при котором достигается равновесие (между численностью населения и природными возможностями среды). Таким образом, мы имеем здесь реализованную

способность к развитию — , но, кроме того, остается и не

реализованная способность: 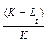. Эта модельрасценивается как весьма перспективная. Конечно, имеются и другие возможности моделирования развития (см. Van Geert, 1994, р.100—101).

Формальная модель приложима к любому материалу, например, к словарному запасу, когнитивному развитию, развитию моральных суждений, развитию социальной адаптации. В логистической модели развития важны на­чальные значения, такие как темп развития и механизмы сдерживания. Действие последних будет, очевидно, ощу­щаться все сильнее по мере приближения развития к пре­дельной точке. В модель могут быть заложены разные темпы развития. Это достигается с помощью методов ком­пьютерной имитации процесса. В итоге подобных упражне­ний иногда появляются результаты, противоречащие интуитивно ожидаемым. Так, в случае высокого темпа раз­вития процесс становится хаотическим: это происходит в случае, если темп развития начинает превышать 2,57. До­пустим, для примера, что на некоторой территории (остро­ве) может выжить максимум 60 кроликов. При начальной их численности в 20 особей и очень высоких темпах приро­ста (например, при темпе равном 3), численность, которую мы получаем в результате, сначала будет превышать 60, а затем внезапно упадет ниже 60 и перейдет в область отри­цательных чисел. Но, поскольку отрицательного поголовья кроликов не бывает, следует признать, что в данных усло­виях эта модель не дает успешных результатов. Модель расширяется с целью моделирования развития двух конку­рирующих форм поведения.

(L и В — две развивающихся формы поведения; х — па­раметр).

Таким образом, развитие одной формы поведения может оказывать влияние (возможно, тормозящее его) на разви­тие другой формы поведения. Многие матери говорят, что интуитивно чувствуют, как начало ходьбы ребенка задер­живает развитие его речи.

 

Модель развития имитируется с помощью компьютера. Модели имеют смысл, если они помогают что-то понять, например, механизмы, действующие в развитии. Так, весь­ма незначительные изменения в начальных, исходных зна-чениях могут привести к весьма значительным последствиям. Происходит хаотический рост. Иногда раз­витие становится непредсказуемым. Здесь уместен часто используемый пример с предсказанием погоды. Весьма ма­лые различия могут вызывать крупные изменения, а на протяжении продолжительного времени —- даже измене­ния хаотического типа, т.е. непредсказуемые изменения. Таким образом, подобный «предиктор развития» может иг­рать лишь весьма скромную роль.

Эти модели могут обогатить психологию развития. Они дают новые понятия, идеи. В них есть место для любых значений переменных. На основе совместного действия процессов может возникнуть новый паттерн. В отношении такого рода паттерна легко возникает соблазн рассматри­вать его как следствие реализации некоего плана. Даже беспорядочные паттерны легко воспринимаются как искус­ственно, специально созданные. Используется понятие «со­стояния притяжения» (attraclor stale). Многие виды смоделированного развития завершаются в момент под­ключения сдерживающих его механизмов. Это и есть своего рода состояние равновесия, к которому «стремится» про­цесс. С этой точки зрения, развитие можно определить как «стабилизацию и дестабилизацию состояний равновесия» (Bogartz, 1994, р.296).

Эти модели переориентируют психологию развития на применение таких переменных, которые допускают неод­нократно повторяющиеся измерения (заметим, что далеко не любую сторону поведения можно подвергать частым из­мерениям): на определение «состояний равновесия», путей и траекторий процессов развития, на контроль за парамет­рами, учет темпов развития, выявление пределов развития и механизмов его сдерживания, на исследование процессов перехода между стадиями. Эти модели должны быть рас­пространены на исследование поведения, эмоциональной и познавательной сферы человека. В настоящее время приме­нение этих моделей ограничивается развитием двигатель­ной сферы и ростом словарного запаса. Возможно, это

окажет свое влияние на систему понятийного описания раз­вития и даже на его диагностику и оценку, измерение. Ди­агностика должна давать прогноз как для групп, так и для отдельных индивидов. Прогноз имеет центральное, ключе­вое значение. Пока же есть основания подозревать, что частично прогноз строится как линейное предсказание (ча­ще всего на основе моделей регрессии), а частично — как интуитивное представление о возможных изменениях («трудности пройдут, сохранятся, усилятся»).

Рассмотренные выше модели обсуждаются также и с кри­тических позиций. Богартс (1994, р.314) отмечает, что эти модели очень легко могут стать настолько сложными, что результаты не будут поддаваться вычислению. Число пара­метров должно быть ограниченным. Понять источники та­кой чрезвычайной сложности нетрудно, если учесть, что каждое значение переменной рассматривается как функ­ция всех предшествующих значений, которые в свою оче­редь зависят от многих параметров. Кроме того, создание кривых роста (развития) иногда имеет вид простой «подгон­ки». Всегда можно с успехом найти модель для совокупно­сти полученных данных. Богартс призывает к использованию новых возможностей, открываемых данны­ми моделями.

Эйслин (1993) критикует технологию нелинейных сис­тем. Он утверждает, что она приложима к ограниченному кругу проблем, и предупреждает об опасности неправомер­ного, расширительного ее применения (р.386). Автор, более того, обращает внимание на то, что в психологии использу­ются термины из физики. Как и Богартс, Эйслин требует, чтобы модели побуждали исследователей к чему-то боль­шему, чем построение соответствующих кривых роста (раз­вития).

Подведем некоторые итоги. Как показано в этом разделе, предпринимаются попытки математического моделирова­ния феноменов развития. Вполне возможно, что со време­нем этот подход окажет существенное влияние на теорию психодиагностики и измерения. Эти модели применимы к таким явлениям, в которых даже весьма малые изменения могут иметь значительные последствия; простые линейные модели, построенные на основе принципа «вход — выход», замещаются, а процесс развития более на зажимают в тес-

 

ную схему причинно-следственной детерминации поведе­ния со стороны его предпосылок. Но в настоящее время влияние этих моделей пока ограничено. Диагностика пока больше направлена на результаты (продукты) развития, а не на процесс и его течение в прошлом и настоящем. Диаг­носты не располагают данными лонгитюдных исследова­ний, что, однако, следует отнести на счет психологии развития.

6.5. Оценка развития: соотношение трех уровней анализа

Первый уровень, т.е. уровень житейских представлений о развитии, исследуется как явление «sui generis»*. Иногда представления неспециалистов сравнивают с результатами объективного тестирования. Кроме того, было бы интересно узнать, могут ли представления о развитии приводить к каким-то специфическим особенностям поведения. Осо­бенно важное значение это имеет для детско-родительских отношений и отношений между учителем и учеником. Крате (1991) приводит пример, когда родители ребенка бы­ли убеждены, что генетически закладывается любовь к та­кому продукту, как брюссельская капуста. Интересно, будут ли через какое-то время эти родители заставлять своего ребенка есть капусту?

Житейские представления и теории развития.

Житейские представления не зависят от теорий разви­тия. Провести их развернутое сопоставление в настоящее время невозможно, поскольку отсутствуют исследования, которые, подобно исследованиям на основе пятифакторной модели в области личностных черт, были бы направлены на основные характеристики развития. Тем не менее Вальси-нер (1985,1986) делает попытку сравнить житейские рас­суждения о развитии с некоторыми признанными теориями развития. Это была его реакция на позицию Смедслунда, который считает, что нет оснований для уверенности, что уровень постановки проблем в научной психологии разви­тия заметно превосходит уровень житейских вопросов, от­носящихся к значению тех или иных психологических конструктов. По мнению Смедслунда, именно семантика

* sui generis (лат.) —особого рода (прим. перев.).

житейских представлений и знаний о развитии лежит в основе теорий развития, последние же ни в чем не превос­ходят их. В свою очередь Вальсинер признал, что психоло­гии как отдельной научной дисциплине было очень трудно подняться выше уровня здравого смысла. Обе формы знания включены в одни и те же социальные, культурные и исто­рические процессы. Однако Вальсинер полагает, что как научная дисциплина психология развития должна предло­жить нечто большее, чем то, что известно на уровне здра­вого смысла. Для этого недостаточно объявить об ошибочности многих житейских представлений по причине их несоответствия научным (методологическим) принци­пам. Житейские представления должны стать предметом исследования, чтобы затем научное и житейское знание использовались бы в определенном сочетании.

Точка зрения Вальсинера, по-видимому, близка к исти­не. В данной книге мы также проводим мысль, что научное и житейское знание несводимы друг к другу. Каждое имеет свою собственную линию и движущие силы. Необходимо их столкновение, причем не направленное на некоторое «уре­гулирование», на деле же мы имеем скорее противополож­ное — стремление достичь взаимного согласия. Можно говорить об их взаимовлиянии. Многие категории теорий развития образуют составную часть повседневного житей­ского языка. Так, многие теории, описывающие жизненный цикл человека, практически прямо «накладываются» на житейские представления.

Теории развития, и психометрические модели.

Как мы уже отмечали, теории и категории психологии развития в значительной мере не соответствуют теоретиче­ским понятиям, на которых построено классическое тести­рование. Шкалы развития, т.е. порядковые шкалы, нельзя анализировать с помощью классических корреляционных методов (т.е. метода факторного анализа и коэффициентов внутренней согласованности).

Порядковые шкалы и другие модели из теории анализа ответов в заданиях открывают возможности для описания основных характеристик развития. Возможны разработки многомерного типа, однако примеры такого рода пока от­сутствуют.

 

Классическая теория тестов и психология развития де­монстрируют противоположные подходы и точки зрения. Эта противоположность.носит очевидный характер в воп­росе об оценке различий. С позиций классического тести­рования развитие можно рассматривать как различие между двумя оценками, проведенными в двух разных слу­чаях. Надежность оценки различий традиционно считается сложным вопросом. Оценка различий тем менее надежна, чем меньше показатели надежности двух измерений. Сте­пень надежности различий между двумя измерениями ока­зывается ниже также и в том случае, если между двумя изменениями имеется корреляция. Это можно видеть в сле­дующей формуле:

где r₁₁, r₂₂ — это коэффициенты надежности, а r₁₂ — ко­эффициент корреляции между двумя измерениями).

Это привело к тому, что на практике оценкой различий не пользуются (Cronbach, Furby, 19970). Уиллет (1988, р. 347), однако, указал на то, что измерение (оценивание) явлений развития и изменений требует иного концептуаль­ного обоснования. Развитие — это процесс, происходящий внутри человека, и необходимо описать траектории инди­видуального развития и объяснить их. Эта позиции согла­суется с принципами математического моделирования развития (Van Geert, 1991, 1994).