Производная логарифмической функции. y=logax
Dy = loga(x+Dx)-logax = loga(1+Dx/x) = 1 loga(1+Dx/x) = 1loga(1+t) = 1 loga(1+t)1/t
Dx Dx Dx x Dx/x x t x
где t=Dx/x Используя непрерывность функции logax в точке х=е и первый замечательный предел, найдём производную логарифмической функции: (logах)¢= 1( logа(lim(1+t)1/t) = 1 logae= 1.
x t®0 x x lna
Производная показательной функции.
У=ах является обратной для функции х=logау. По теореме
у¢х= 1 = 1 =ylna
x¢y 1/ylna
Поскольку у=ах, получаем (ах)¢=ахlna.
Производная степенной функции.
Функция у=ха при х>0 может быть представлена в виде ха=еalnx. Найдём (ха)¢=(еalnx)¢= еalnx(alnx)¢=ха*а/х=аха-1 Аналогично доказывается для x<0.
Производные тригонометрических функций.
С помощью формулы sinа-sinb=2sin[(a-b)/2]*cos[(a+b)/2], первого замечательного предела и непрерывности функции cos x найдём
(sinх)¢=lim sin (х+Dх) – sinх = lim 2sin(Dх/2) cos(х+Dх/2) =
Dx®0 Dx Dx®0 Dx
=lim sin(Dх/2) cos(х+Dх/2) = cos x
Dx®0 Dx/2
Для нахождения производных функций cos x и tg x можно использовать тождество cos x=sin(x-p/2), правило дифференцирования сложной функции.
Итак, (sin х)¢=cos x, (cos x)¢= - sin x, (tg x)¢=1/cos2 x.
Производные обратных тригонометрических функций.
Функция у=arcsinx является обратной для функции х=sinу. Следовательно, (arcsinx)¢x= 1 = 1 = 1 = 1
(siny)¢y cosy Ö1-sin2xØ Ö1-x2Ø
Аналогично находятся остальные обратные тригонометрические функции. (arcsinx)¢=1/Ö1-x2Ø, (arccosx)¢= - 1/Ö1-x2Ø, (arctgx)¢=-1/(x2+1).
12. Правило Лопиталя
Теорема (правило Лопиталя). Пусть А – число, символ одностороннего предела (А=а±0) или символ бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно малые, либо обе бесконечно большие при х→А. Тогда, если существует предел
(конечный или бесконечный),
то существует и предел при этом выполняется равенство:
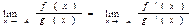
Доказательство:
Доказательство теоремы дадим в случае, когда ƒ(х) и g(х) – бесконечно малые функции и А=а – число. Изменим, если это необходимо, определение функций ƒ(х) и g(х) в точке а так, чтобы значения этих функций в точке а были бы равны нулю: ƒ(х) = g(х)=0. Так как
и
то ƒ(х) и g(х) непрерывны в точке а,и к этим функциям можно применить теорему Коши. Учитывая, что ƒ(а) = ƒ(b)=0, получим
для некоторой точки с, расположенной между точками а и х. При х→а имеем с→а и, следовательно если ƒ(х)→0 и g(х)→0 (соответственно, |ƒ(х)|→+∞, |g(х)|→+∞), когда а→А. Правило Лопиталя позволяет во многих случаях найти предел вида
или, иными словами, раскрыть неопределенность.
В ряде случаев по правилу Лопиталя удается раскрыть неопределенности вида
Для этого следует воспользоваться тождеством
которое приводит указанные неопределенности к виду 0•х.
