Припустимо, що на деякій території мешкають два види популяцій: жертви і хижаки. Нехай х – число жертв, у – число хижаків. Використовуючи модель Мальтуса з необхідними поправками, що враховують поїдання жертв хижаками, приходимо до наступної системи, що носить ім'я Вольтерра - Лотки:
(4.5)
Ця система має рівноважний стан, коли число жертв і хижаків постійно. Відхилення від цього стану призводить до коливань чисельності жертв і хижаків, аналогічним коливанням гармонійного осцилятора. Як і у випадку гармонійного осцилятора, це поведінка не є структурно стійкою: мала зміна моделі (наприклад, що враховує обмеженість ресурсів, необхідних жертвам) може привести до якісної зміни поведінки. Наприклад, рівноважний стан може стати стійким, і коливання чисельності будуть затухати. Можлива і протилежна ситуація, коли будь-яке мале відхилення від положення рівноваги призведе до катастрофічних наслідків, аж до повного вимирання одного з видів. На питання про те, який з цих сценаріїв реалізується, модель Вольтерра - Лотки відповіді не дає: тут потрібні додаткові дослідження.
Розглянемо модифікацію системи моделі хижак-жертва, в котрій навіть за відсутності хижаків чисельність популяцій жертв обмежується внутрішньовидовою конкуренцією. Система рівнянь, що описують динаміку популяцій, має вигляд:
Член 
, пропорційний кількості зустрічей між особинами, враховує «само обмеження» популяції,що пояснюється багатьма факторами (конкуренція всередині популяції, нестача місця або їжі, передача інфекції через тісноту, тощо). Знайдемо особливі точки у вигляді:
Зауважимо, що фазові траєкторії перетинають пряму 
в горизонтальному напрямку, так як на цій прямій 
. Пряму 
фазові траєкторії перетинають у вертикальному напрямку, так як на цій прямій 
.
Очевидно, що система має три особливі точки:
1. 
2. 
3. 
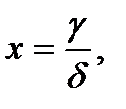
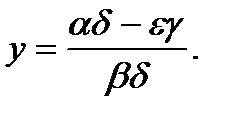
Детально розглянемо випадок, коли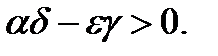 
Випадок 
залишимо для самостійного вивчення.
1. Розглянемо поведінку системи поблизу першої особливої точки. Нехтуючи величинами другого порядку малості 
та 
, маємо
Матриця коефіцієнтів правої частини цієї системи диференціальних рівнянь має вигляд
М= 
.
Її визначник detM = 
, отже, перша особлива точка – сідло.
2. Тепер розглянемо поведінку системи поблизу другої особливої точки. Нехай 
, де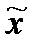 
– мала величина. Тоді система рівнянь поблизу особливої точки приймає вигляд:
Нехтуючи доданками другого порядку малості, маємо:
Матриця коефіцієнтів правої частини системи диференційних рівнянь має вигляд:
М= 
.
Її визначник detM = 
, оскільки за припущенням 
. Отже, друга особлива точка – також сідло. Поблизу цієї особливої точки фазові траєкторії являються гіперболами. Знайдемо їх асимптоти. Для цього перепишемо систему рівнянь у вигляді одного рівняння:
.
Підставимо в нього 
.
Звідки 
, тобто одна з асимптот y=0, а друга – 
.
3. Тепер розглянемо поведінку системи поблизу третьої особливої точки. Нехай 
, 
, де 
, 
– малі величини. Тоді, система диференціальних рівнянь записується у вигляді:
Нехтуючи доданками другого порядку малості, маємо
Матриця коефіцієнтів правої частини цієї системи диференціальних рівнянь має вигляд:
М= 
.
Визначник матриці detM = 
, слід матриці trM= 
, отже, особлива точка – стійкий фокус або вузол.
В розглянутій моделі приріст чисельності біомаси представлений членом 
. Це відповідає лише тим популяціям, розмноження яких здійснюється шляхом самозапліднення (мікроорганізми). Якщо ж в основі розмноження лежить схрещування, що передбачає зустрічі між особинами різних статей одного й того ж виду, то приріст буде тим вищій, чим більша кількість зустрічей між особинами, а останні пропорційні квадрату чисельності популяції. І таким чином, для різностатевої популяції в умовах необмежених ресурсів можна записати:
. (4.6)
Рівняння (4.6) добре описує той факт, що при низькій щільності популяцій швидкість розмноження різко спадає, тому що ймовірність зустрічей двох особин різних статей зменшується при зниженні щільності популяції пропорційно квадрату густини. Однак при великій щільності популяцій швидкість розмноження лімітує вже не число зустрічей особин протилежної статі, а число самок в популяції. Формула, що враховує ці обидва факти, має вигляд:
. (4.7)
В формулу (4.7) можна ввести член, пропорційний чисельності і описуючий смертність:
.
Ця модель враховує той факт, що при спаданні щільності популяції нижче критичної межі середній час, протягом якого може здійснитися запліднення, стає більшим за час життя окремої особини, точніше за час, протягом якого особина здатна до розмноження. В цьому випадку популяція вимирає. Величина нижчої критичної густини різна для різних видів. Спостереження біологів показали, що це лише одна пара особин на тисячу квадратних кілометрів у випадку ондатр і сотні тисяч особин для американського мандрівного голуба. Очевидно, що модель взаємодії двох популяцій не описується лише наведеними рівняннями.
Серед основних типів взаємодій популяцій виділяють наступні:
– міжвидова конкуренція (за їжу, місце існування і т.і.), що веде до зниження чисельності обох видів;
– відношення типу хижак – жертва (або паразити – хазяїн), при яких зростання чисельності одного виду (хижака) веде до зменшення другого виду(жертви);
– симбіоз, що веде до збільшення чисельності обох видів.
Крім наведених виділяють: нейтралізм, паразитизм, хижацтво, протоко операція (взаємодія корисна для обох популяцій, але не обов’язкова), мутуалізм (обов’язкова взаємодія, корисна для обох видів). Всі ці типи накладають свій відбиток на математичну модель, що описує процес взаємодії двох популяцій.
Зауважимо, що аналогічні типи взаємодій виникають в економіці між учасниками ринку товару, які можуть займати одну й ту саму нішу на ринку цього товару, конкурувати між собою або плідно співпрацювати.
Описуючи різні природні та експериментальні ситуації, різні автори пропонували велику кількість моделей, праві частини рівняння яких представляли собою деякі функції чисельності досліджуваних популяцій. Вигляд цих функцій визначався, виходячи з конкретної експериментальної ситуації. У зв'язку з цим виникло питання про вироблення деяких загальних критеріїв, що дозволяють встановити, якого виду функції можуть описати ті чи інші особливості поведінки чисельності взаємодіючих популяцій, зокрема стійкі коливання. Ці роботи розвивалися за двома напрямками. Представники
першого напряму, описуючи входять в модельні системи функції, задають лише якісні особливості цих функцій, такі як додатність, монотонність, відносини типу більше-менше.
У рамках другого напрямку послідовно розглядалися різні модифікації системи Вольтерра, одержувані включенням у вихідну модель різних додаткових чинників і закономірностей, що описуються явними функціями. Синтез обох напрямків передбачає такі етапи.
1. Виявлення основних біологічних факторів і закономірностей, які слід брати до уваги при моделюванні системи двох взаємодіючих популяцій. Підбір математичних функцій, задовільним чином описують ці взаємодії.
2. Аналіз динамічних ефектів, до яких призводить врахування окремо взятих факторів.
3. Побудова та дослідження набору моделей системи взаємодіючих видів, що включають різні комбінації основних біологічних факторів, що впливають на динаміку системи.
4. Виявлення особливостей, спільних для різних моделей, і формулювання загальних тверджень про структуру динамічної поведінки в таких системах.
У найзагальнішому вигляді система рівнянь взаємодії двох популяцій може бути представлена у вигляді:
(4.8)
Тип відношень між популяціями накладають на функції 
певні умови. Так, наприклад, якщо популяція знаходиться в конкурентних взаємодіях, то виконуються нерівності
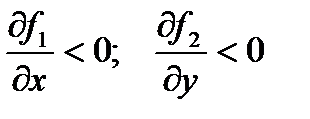для всіх 
.
Найбільш часто застосовуються моделі, що передбачають пропорціональну залежність функцій від численності відповідних популяцій:
(4.9)
Іноді припускають, що швидкість поїдання жертв залежить від щільності популяцій жертв і хижаків, причому від популяції хижаків – пропорційно її чисельності:
(4.10)
Для різних цілей дослідження можуть бути обрані різні типи умов, що накладаються на функції 
та 
. В таблиці 4.1 наведені вирази для цих функцій, які застосовуються в різних моделях для опису конкуренції самих різноманітних видів. Зміст використаних параметрів наступний: 
– природня швидкість зростання і -ої популяції; 
– ємність середовища і -ого виду за відсутністю другого виду; 
– міра внутрішньовидової конкуренції; 
– міра міжвидової конкуренції; 
– параметр, що враховує зміну функції зростання залежно від густини; параметр 
– не має точного біологічного змісту і враховує взаємодії другого порядку.
Таблиця 4.1. Різні моделі співтовариства «хижак – жертва» [11]
| 
| 
| автори |
| 
| 
| Вольтерра, Лотка |
|
| 
| Гаузе |
|
|
| Нікольсон – Бейлі |
|
|
| 
| Пієлоу |
|
| 
| 
| Холлінг |
|
| 
| 
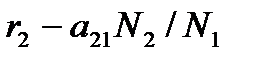
| Івлєв |
|
| 
|
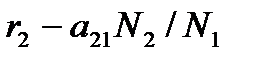
| Рояма |
| 
| 
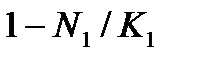
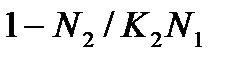
| Шимазу і др. |
| 
| 
| Май |
Слід відзначити, що існують також моделі екосистем із двох видів, взаємодіючих по типу «хижак – жертва» з урахуванням вікової структури популяцій і впливу передісторії системи на динаміку щільності популяцій (рівняння із запізненням); моделі, які враховують просторові переміщення (рівняння в частинах похідних).
Варіанти завдань
| № варіанту | Постановка задачі |
| Вивести рівняння руху маятника без опору. Для випадку, коли всі сталі, які входять до рівняння, дорівнюють 1, накреслити траєкторії на фазовій площині. Дати фізичне тлумачення траєкторіям різних типів. | |
| Вивести рівняння руху маятника з опором, пропорційним квадрату швидкості. Накреслити траєкторії на фазовій площині. Для випадку, коли всі сталі, які входять до рівняння, дорівнюють 1, накреслити траєкторії на фазовій площині. Дати фізичне тлумачення траєкторіям різних типів. | |
| Вивести рівняння руху маятника, на який діє сила, яка дорівнює ½ ваги маятника та спрямована завжди в одну сторону по дотичній до дуги окружності, по якій рухається маятник. Прийнявши сталі l та g за 1, намалювати траєкторії рівняння на фазовій площині. Які рухи маятника зображуються траєкторіями різних типів? | |
| Вантаж масою m прикріплений до пружини. При відхиленні вантажу на відстань x пружина діє на нього з силою kx, спрямованою до положення рівноваги. Сила тертя дорівнює f=cosnt та спрямована в сторону протилежну до швидкості вантажу. Коли t=0 вантаж знаходиться на відстані h від положення рівноваги та має нульову швидкість. Вивести рівняння руху вантажу. Прийнявши m=2, k=2, f=1, h=5, зобразити рух вантажу на фазовій площині. | |
Записати математичну модель розгойдування гойдалки. Зобразити на фазовій площині малі коливання гойдалки змінної довжини, вважаючи, що при русі гойдалки угору її довжина дорівнює l, а при русі вниз дорівнює L>l. У скільки разів збільшиться амплітуда за одне повне коливання? (Вказівка: при малих коливаннях вважати  . Зміна довжини гойдалки проходить миттєво (стрибком), при цьому кут відхилення гойдалки та її момент кількості руху відносно вісі не відчувають стрибків).
| |
| Існує три популяції: жертва, хижак та суперхижак. Чисельність жертв в умовах відсутності хижаків росте за логістичною моделлю (росте пропорційно чисельності і спадає пропорційно квадрату чисельності). Хижаки харчуються жертвами, причому при винищуванні жертв і при розмноженні хижаків враховується ефект насичення хижаків (збільшення чисельності жертв, починаючи з певного рівня, не призводить до збільшення їх споживання хижаками). За відсутністю жертв хижаки вимирають експоненційно. Суперхижаки існують за рахунок споживання хижаків, при цьому також враховуються ефекти насичення і вимирання за умови відсутності їжі. Побудувати і дослідити модель співіснування популяцій. | |
Описати динаміку температури 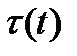 повітря у приміщенні, в якому є радіатор і кондиціонер.  – швидкість зростання температури всередині будівлі, пов’язана із роботою радіатора;  – швидкість зміни температури, пов’язана із роботою кондиціонера;  – температура зовні (вважається заданою). Вказівка: закон охолодження Ньютона – швидкість зміни 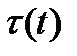пропорційна різниці температур  .
Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати
| |
Записати модель раціонального використання врожаю (поодинокої природньої популяції):  – чисельність популяції; 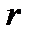 – темп приросту (питома лінійна швидкість зростання);  – ємність середовища;  – кількість зібраного врожаю за одиницю часу ( – міра активності промислу). Записати динаміку чисельності популяції.
Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати
| |
| Побудувати просту модель національної економіки, в якій описати динаміку зміни національного доходу І і розміру споживчих витрат С з урахуванням розміру урядових витрат G, припускаючи що швидкості зміни величини національного доходу і розміру споживчих витрат пропорційні самому НД і споживчим витратам з відповідними коефіцієнтами пропорційності 1<a<¥; 1£b<¥. Модель повинна стосуватися області природної зміни змінних: І³0, С³0. Показати, що коли рівень урядових витрат постійний, G= G0, то існує стан рівноваги. Визначити характер нерухомої точки при b=1 і показати, що тоді економіка відчуває коливання. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати | |
Дослідити найпростішу модель управління молекулярними процесами в клітині, яка описує зміну кількості Х – транспортної рибонуклеїнової кислоти і У – кількості відповідного ферменту. Динамічні рівняння мають вигляд
де  – додатні константи. Довести, що обидві величини Х і У відчувають незгасаючі коливання, що залежать від часу.
Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати
| |
| Дослідити поведінку системи «хижак – жертва», що описується моделлю Нікольсон – Бейлі при різних значеннях параметрів. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати | |
| Дослідити поведінку системи «хижак – жертва», що описується моделлю Холлінга. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати | |
| Дослідити поведінку системи «хижак – жертва», що описується моделлю Івлєва. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати | |
| Побудувати нелінійну модель співіснування виробників однотипових товарів (подібних за ціною та якістю), споживачами яких є певний прошарок суспільства з приблизно однаковим рівнем накопичувань (чи доходів), які мешкають в однакових умовах та мають однакову шкалу побажань. Виробники товарів іншої якості співіснують у іншій ринковій ніші. Ввести досліджувані змінні M 1 і M 2 – оборотні кошти першої і другої фірм відповідно, коефіцієнти a 1, a 2, b, c 1, c 2, k 1, k 2, які залежать від періоду обороту і собівартості товару (для кожної з фірм) і параметрів функції попиту. Прибуток фірм входить в рівняння лінійно, білінійні члени можуть описувати збитки, пов’язані із конкуренцією, насиченість ринку може описуватися квадратичними доданками в рівняннях. Передбачити можливість наявності постійних витрат. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати | |
| Побудувати просту модель національної економіки, в якій описати динаміку зміни національного доходу І і розміру споживчих витрат С з урахуванням розміру урядових витрат G, припускаючи що швидкості зміни величини національного доходу (НД) і розміру споживчих витрат пропорційні самому НД і споживчим витратам з відповідними коефіцієнтами пропорційності 1<a<¥; 1£b<¥. Модель повинна стосуватися області природного зміни змінних: І³0, С³0. Нехай урядові витрати пов'язані з національним доходом співвідношенням G= G0 + kІ, де k>0. Знайти верхню межу К для коефіцієнта k, нижче якої існує положення рівноваги в природному області зміни змінних. Описати стан і характер цієї нерухомої точки для b>1. при наближенні k до критичного значення К. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати | |
| Побудувати математичну модель розповсюдження епідемій, яка описує зміну числа сприйнятливих до хвороби і кількості осіб, які захворіли, у відповідних масштабах. Припустити, що: число сприйнятливих до хвороби: 1) лише зменшується пропорційно кількості зустрічей з хворими; 2) зменшується як в 1) і зростає з постійною швидкістю. Як додаткова складова у диференціальному рівнянні впливає на розвиток епідемії? Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати отримані результати | |
Дослідити математичну модель, що описує процеси взаємодії двох нервових клітин в нейронній мережі. Ця модель є системою двох диференціальних рівнянь
де  – параметри, а
 .
Побудувати біфуркаційну множину, перерахувати можливі способи динамічної поведінки цієї системи. Представити фазовий портрет для деяких значень параметрів.
| |
| Дослідити поведінку системи «хижак – жертва», що описується моделлю Гаузе. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати | |
| Побудувати модель конкуренції двох виробників товарів довготривалого користування. Фірми виробляють і продають взаємозамінні товари однакової якості, що знаходяться в одній ринковій ніші (у споживачів немає апріорних переваг, товари купуються без урахування знака фірми). Передбачається, що функція попиту лінійна і має ціновий поріг, вище якого товар не споживається (функція попиту життєво необхідних товарів такого порогу не має, і конкуренція протікає за іншим сценарієм). На ринку встановлюється єдина ціна. Конкурентна боротьба ведеться лише ринковими методами. Товарний баланс встановлюється швидко (товар не накопичується на складах), час обороту товарів на ринку істотно менше часу виробничого циклу. Цінова рівновага встановлюється також швидко. Записати рівняння динаміки оборотних коштів (балансу прибутків і витрат) в умовах зроблених припущень Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати | |
Показати, що заміна змінних 
перетворює систему диференціальних рівнянь, що описує процеси взаємодії двох нервових клітин в нейронній мережі (варіант 17) на наступну
яка містить лише три параметри
 .
Дослідити систему.
| |
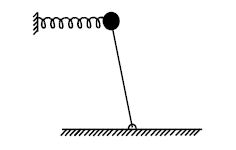
Маятник у верхньому положенні рівноваги прикріплений до нелінійної пружині (див. рис.). Нелінійність пружини описується співвідношенням F = kx + cx3, де k і c - додатні коефіцієнти. Кут відхилення маятника від вертикалі малий, довжина стрижня l, маса кульки m. Якою з універсальних моделей нелінійного осцилятора слід користуватися при lk> mg і при lk < mg? Отримайте рівняння відповідних моделей в явному вигляді, оцініть поправку до частоти і величину зміщення центру коливань щодо положення рівноваги. Амплітуда коливань A.
Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати
| |
| На рис. варіанта 20 показана система, що є маятник у верхньому положенні рівноваги, прикріплений до пружини. Покажіть, що коли пружина лінійна і її коефіцієнт жорсткості k невеликий, то положення рівноваги нестійке. Покажіть, що якщо пружина нелінійна, то в системі можлива бістабільність – реалізуються два положення сталої рівноваги. Вважайте, що нелінійність пружини описується співвідношенням F = kx + cx3, k і c – додатні коефіцієнти, а кут відхилення маятника від вертикалі малий. Довжина стрижня l, маса кульки m. (Вказівка: отримайте в явному вигляді залежність потенційної енергії маятника від координати х). Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати | |
| Дослідити поведінку системи «хижак – жертва», що описується моделлю Рояма. Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати | |
| Дослідити поведінку системи «хижак – жертва», що описується моделлю Шимазу. Побудувати біфуркаційну множину. Проінтерпретувати результати | |
Невелике тіло маси m може ковзати без тертя по горизонтальному стержню (див. рис.). Тіло прикріплене пружиною жорсткості k до точки O, що знаходиться на відстані l від стрижня. Довжина пружини в не розтягнутому стані l0, причому l0 > l. Знайти положення рівноваги і відповідні їм значення потенціальної енергії. Побудуйте графік функції U (x), який надає залежність потенціальної енергії від координати тіла, і за його допомогою визначити, які з положень рівноваги стійкі. Побудувати фазовий портрет системи. Вказати характерні елементи фазового портрету: особливі точки, типові траєкторії.
Напишіть рівняння сепаратриси в явній формі. Використовуючи графік потенційної енергії, опишіть поведінку тіла, що відповідає перерахованим елементів фазового портрету.
Побудувати біфуркаційну множину. Побудувати фазовий портрет для певного набору параметрів. Проінтерпретувати результати
|
СПИСОК ЛІТЕРАТУРИ
1. Амелькин В.В. Дифференциальные уравнения в приложениях. – М.: Наука, 1987. – 160 с.
2. Арнольд В. И. Обыкновенные дифференциальные уравнения. –М.: Наука, 1984.
3. Арнольд В. И. Математические методы классической механики. — М.: Наука, 1986.
4. Арнольд В. И. Теория катастроф. — М.: Наука, 1986.
5. Баутин Н. Н., Леонтович Е. А. Методы и приемы качественного исследлвания динамических систем на плоскости. — 2-е изд., доп. — М.: Наука, 1990. — 488 с.
6. Егоров А. И. Обыкновенные дифференциальные уравнения с приложеними. – 2-е изд., испр. _ М.: ФИЗМАТЛИТ, 2005. – 384 с.
7. Марри Дж. Нелинейные дифференциальные уравнения в биологии. Лекции о моделях: Пер. с англ. – М.: Мир, 1983. – 396 с.
8. Моисеев Н. Н. Асимптотические методы нелинейной механики. — М.: Наука, 1986.
9. Пантелеев А. В ., Якимова А.С., А.В. Босов. Обыкновенные дифференциальные уравнения в примерах и задачах: Учебное пособие. – М.: Изд-во МАИ, 2000. – 380 с.
10. Полуэктов Р. А., Пых Ю.А., Швытов И.А. Динамические модели экологических систем. – Л., 1980.
11. Понтрягін Л. С. Звичайні диференціальні рівняння. — К., 2000.
12. Ризниченко Г.Ю., Рубин А.Б. Биофизическая динамика продукционных процессов. – Москва-Ижевск: Институт компьютерных исследований. 2004. – 464 с.
13. Сергеева Л. Н. Моделирование структуры экономических систем и процессов. — Запорожье, 2002.
14. Федорюк М. В. Звичайні диференціальні рівняння. — К., 1999.
15. Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложеними: Пер. с англ.– М.: Мир, – 243 с.
16. Алексеєв-Сухоруков. Теория катастроф. – М., 2009. – 252 с.
