Приклад визначення катастрофи, що описується заданою функцією у виродженій критичній точці

 

Дана функція:

f = xyzt + xyz + xy

1) Знайти вироджені критичні точки К* та розщепити в них функцію.

2) Необхідно визначити катастрофу, що описується даною функцією в виродженій критичній точці, опираючись на пораховані значення corank(f), codim(f) та використовуючи визначник катастроф.

 

Розв’язання:

1) f = xyzt + xyz + xy

Критичні точки:

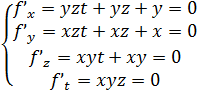K:

Знайдемо матрицю Гессе на цій множині

Таким чином , , K*=K=(0,0,0,0), буде залежати від двох змінних.

Тепер займемось самим розщепленням. Будуємо нову функцію , яка є композицією вихідної функції і дифеоморфізма

де за змінними функція не вироджена, а є неявні функції, які знаходяться з системи рівнянь

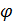Маємо і дифеоморфізм має вигляд

тобто це тотожне перетворення і . А це значить, що функція вже розщеплена, оскільки

Відповідно існує невироджена заміна змінних, яка приводить функцію просто до морсівського сідла. Маємо

Зробимо заміну змінних таку, що

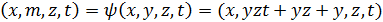
Обчислимо Якобіан

тобто заміна правомірна. В її результаті функція приймає вид .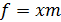

Роблячи заміну змінних

одержимо:

 

2)

Критична точка:

K:

Знайдемо матрицю Гессе на цій множині

Таким чином , , K*=K=(0,0).

Обчислимо codim. Зображуємо «діаграму Ньютона», яка представляє собою сітку, вузли перетину якої відповідають степеням одночленів. Тоді відмітимо перший утворюючий одночлен xy точкою на перетині ліній 1,1. Відкинемо тіні від неї (вправо та вгору – див. рис. 3.2).

Рис. 3.2. Діаграма Ньютона

Наступна похідна . Відмітимо кружками та поєднаємо їх лінією – це і є лінійка Ньютона. Для того, щоб знайти мономи (одночлени), від яких треба відкидати тіні, будемо зрушувати лінійку паралельно самій собі (дозволяється її рухати тільки вправо і вгору – в сторону збільшення степенів x і y). Як тільки один з кружків потрапляє у тінь від одночлена ху, то другий кружок вказує на одночлен, від якого вже можна відкидати тінь.

В нашому випадку, переміщуючи лінійку вгору на одну клітинку, отримаємо, що нижній кружок потрапляє в тінь ху, верхній кружок при цьому знаходиться в 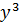і від нього можна відкинути тінь. Переміщуючи тінь з вихідного положення вправо на одну клітинку, також знаходимо ще один моном, від якого можна відкинути тінь: 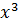. В результаті отримуємо образ ідеалу на діаграмі Ньютона такий як зображено на рисунку.

 

Поза ідеалом залишилось 5 вузлів перетинів. Один з них (0,0) нас не цікавить, так як відповідає константі, які ми не розглядаємо. Крім того, одночлени пов’язані через похідну , тобто задають, по суті, лише один напрямок у додатковому просторі . Тому ковимірність функції . І у якості універсальної деформації можна взяти

Скористаємося таблицею для визначення типу катастрофи – це гіперболічна омбіліка.

 

Варіанти завдань

1. Знайти вироджені критичні точки К* та розщепити в них функцію.

1.1. f = x² + 2xy + yz²

1.2. f = sin²xcosy – y³cos2z

1.3. f = e – x²(z² + sin²y) + 2cosy(z⁴ + 1)

1.4. f = x(x/2 + sin3y)e ^{- z^3}

1.5. f = (xy – z³)(1 – t²) + xz

1.6. f = xy(z + 1)(x – y)z²

1.7. f = y²e^{x^2} – xyz

1.8. f = xu² + y(u + v²)

1.9. f = xyzt + ty + xyt

1.10. f = xy(z + 1) + (x - y)z²

1.11. f = sin²xcos²y – y³cos2z

1.12. f = x³ + 2xy + yz

1.13. f = sin(x²y) + sin(y²z) – sin(z²x)

1.14. f = x(x/3 - sin6y)e ^{- z^3}

1.15. f = sin²xcos4y – y²cosz

 

2. Необхідно визначити катастрофу, що описується даною функцією в виродженій критичній точці, опираючись на пораховані значення corank(f),, codim(f) та використовуючи визначник катастроф.

2.1. f = x⁴

2.2. f = x⁵

2.3. f = x⁶

2.4. f = x⁷

2.5. f = x²y + y⁴

2.6. f = x²y – y⁵

2.7. f = x²y + y⁵

2.8. f = x³ + y⁴

2.9. f = sin(y²) – cos(x²)

2.10. f = [cos(y²) - cosx]ln[(1 + y)²]

2.11. f = x²y - y⁴

2.12. f = x³y + y³

2.13. f = x²y + y⁶

2.14. f = x⁴y – y³

2.15. f = xy³ + х⁴

Відповіді

 

1.

1.1. K* = (0,0,0), f = u² – v² + (1/4)z⁴

1.2. K* = (0,0,z), f = u² – y³cos2z

1.3. K* = (x,0,0), в K₁* = (0,0,0) f = u² + 2cosy + sin²ye ^{- x^2}

1.4. K* = (0,0,z), f = u² – (1/2)sin⁶ye ^{- z^3}

1.5. K* = (0,0,0,t), f = u² – v² + z³(t² - 1)

1.6. K* = (0,0,0), f = u² – v² + w⁴

1.7. K* = (0,0,z), K₁* = (0,0,0) f = u² – (1/4)x²z²e ^{- x^2}

1.8. K* = (x,0,0,0), f = s² – t² + xv⁴

1.9. K* = (0,0,0,0), f = u² – v²

2.

2.1. Зборка Уітні

2.2. Хвіст ластівки

2.3. Метелик

2.4. Вігвам

2.5. Параболічна омбіліка

2.6. Друга еліптична омбіліка

2.7. Друга гіперболічна омбіліка

2.8. Символічна омбіліка

2.9. Зборка Уітні

2.10. Друга еліптична омбіліка