Для побудови фазового портрету лінійної динамічної системи:
необхідно виконати наступні дії:
1. Обчислити detM, де 
, знайти власні значення 
матриці М та обчислити trM 
. Визначити тип особливої точки згідно викладеного у попередньому параграфі матеріалу.
2. Знайти рівняння особливих напрямків (dx/dt)=0 та (dy/dt)=0
y=(-a/b)x, y=(-c/d)x.
3. Якщо особлива точка є сідлом або вузлом, то знайти асимптоти, використовуючи підстановку y=kx.
4. Визначити напрямки фазових траєкторій.
Приклад 1: дослідити характер особливої точки (0,0):
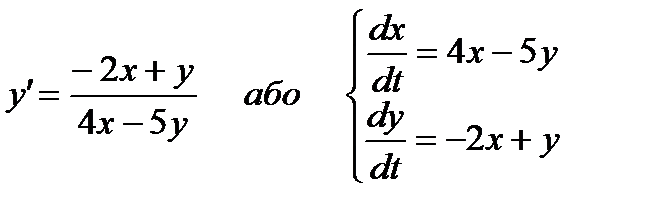(1.13)
1. Обчислюємо визначник і слід матриці М: 
.
Особлива точка (0,0) – сідло. Про цей факт свідчать і корені характеристичного рівняння 
: 
.
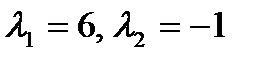2. Рівняння особливих напрямків: y=(4/5)x; y=2x. Першу пряму фазові траекторії перетинають у вертикальному напрямку, а другу – горизонтальному.
3. Знаходимо рівняння асимптот. Нехай y=kx. Розв'язуючи рівняння відносно k: k=(–2+k)/(4–5k), знаходимо кутові коефіцієнтиасимптот: у=(-2/5)x; y=x.
4. Визначаємо напрямки фазових траєкторій, враховуючи знак похідних 
і 
в точках фазових траєкторій.
Рис. 1.9. Поле напрямків системи (1.13) Рис. 1.10. Фазові траєкторії системи (1.13)
Приклад 2: знайти всі нерухомі точки нелінійної системи і дослідити їх
на стійкість
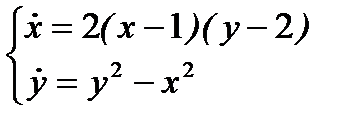. (1.14)
Особливі точки системи знайдемо, розв'язуючи систему рівнянь:
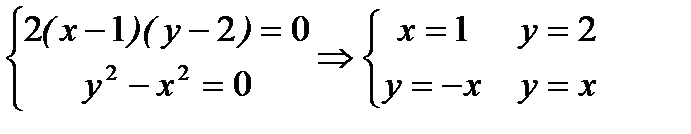
Особливі точки: 
=(1;-1); 
=(1;1); 
=(2;-2); 
=(2;2).
Запишемо вирази частинних похідних функцій 
і 
:
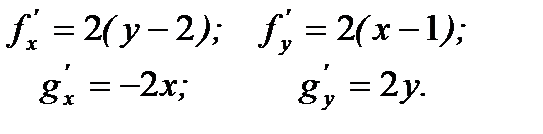
Визначимо тип кожної особливої точки.
I. = (1;-1) – стійкий вузол. Дійсно, лінеаризуючи систему у околі цієї точки, приходимо до системи лінійних диференціальних рівнянь відносно збурень фазових координат:
. (1.15)
На рис. 1.11 наведені фазові траєкторії і поле напрямів цієї системи.
Рис. 1.11. Фазові траєкторії і поле напрямків системи (1.15)
II. =( 1;1 ) – сідло. Лінійна система відносно лінеарізованих фазових змінних в точці (1,1) має вигляд:
(1.16)
На рис. 1.12 наведені фазові траєкторії і поле напрямів цієї системи.
Рис. 1.12. Фазові траєкторії і поле напрямків системи (1.16)
III. =(2;–2) – також є сідлом. Лінійна система диференціальних рівнянь відносно збурень фазових координат в точці має вигляд:
Фазові траєкторії і поле напрямів в цій точці наведені на рис. 1.13.
Рис. 1.13. Фазові траєкторії і поле напрямків системи (1.14) у околі точки (2;–2)
IV. =(2;2) – нестійкий фокус, тому що в лінійній системі диференціальних рівнянь відносно збурень 
; 
; 
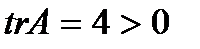(корені характеристичного рівняння: 
). Фазові траєкторії і поле напрямів наведені на рис. 14.
Рис. 1.14. Фазові траєкторії і поле напрямків в точці системи (1.14) у околі точки (2;–2)
Фазовий портрет динамічної системи (1.10) представлений на рис. 1.15.
Рис. 1.15. Фазовий портрет системи (1.14)
