Тема 8. Показатели качества САУ и их коррекция

 

Качество системы САУ определяется качеством переходного процесса, которое оценивают по переходной функции h(t), представляющей собой реакцию системы на внешнее воздействие типа единичной ступенчатой функции 1(t).

На примере переходной функции колебательного звена рассмотрим основные показатели качества переходного процесса: время регулирования, перерегулирование, частоту колебаний, число колебаний, максимальную скорость и максимальное ускорение регулируемой величины.

 

 

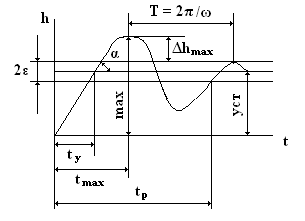
Время регулирования t_p определяет длительность переходного процесса. Теоретически переходной процесс длится бесконечно долго, однако он заканчивается практически, как только отклонение регулируемой величины от установившегося значения не будет превышать допустимых пределов ε = (3-5)%∙h_уст. Временем регулирования характеризуют быстродействие системы. Однако иногда быстродействие системы характеризуют временем t_у достижения переходной функцией первый раз установившегося значения или временем t_max достижения максимального значения h_max.

Перерегулирование Δh_max или выброс представляет собой максимальное отклонение регулируемой величины от установившегося значения. Обычно, первый максимум является наибольшим. Относительное перерегулирование определяется следующей формулой:

ε = Δh_max∙100% / h_уст. (1)

 

Время регулирования и перерегулирование тесно связаны между собой. Перерегулирование появляется вследствие того, что система к установившемуся состоянию подходит с определенной скоростью, которая определяется тангенсом угла наклона α касательной в точке, соответствующей времени t_у: Δh/Δt = tgα при t = t_y.

Чем больше эта скорость (круче кривая переходной функции), тем больше будет перерегулирование Δh_max. Для уменьшения перерегулирования необходимо снизить скорость, с которой система подходит к установившемуся состоянию, что приведет к увеличению времени регулирования t_p. Если система подходит к установившемуся состоянию с нулевой скоростью, то перерегулирования не происходит, но время регулирования значительно возрастает. Таким образом, можно сделать вывод, что, как отсутствие, так и очень большое перерегулирование являются нежелательными. Поэтому перерегулирование допускают в пределах 20-30% от установившегося значения. При этом число полупериодов колебаний переходной функции равно двум-трем.

Качество переходного процесса оценивают на основе анализа кривой переходной функции. Однако на практике при анализе качества регулирования часто используют косвенные оценки, которыми являются некоторые числа, характеризующие отдельные моменты переходного процесса и которые можно найти без построения графика переходного процесса. Рассмотрим некоторые из косвенных оценок.

Частотные оценки. Для оценки используется относительная АЧХ в виде зависимости отношения H(ω)/К от частоты ω: Δ(ω) = H(ω)/К.

 

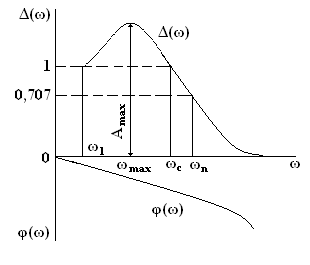
Относительная АЧХ на резонансной частоте ω_max имеет максимум, соответствующий значению Δ(ω_max) = Δ_max. При дальнейшем увеличении частоты система вследствие своей инерционности не успевает реагировать на колебания больших частот иΔ(ω) резко «падает».

Установлено, что чем больше Δ_max, тем более колебательным является переходной процесс. Отношение Δ_max/Δ(0) = М называют показателем колебательности. Для следящих систем Δ(0) = 1, поэтому М = Δ_max. Обычно М = 1,2 – 1,5. При малых М система имеет большое время регулирования. При больших М увеличивается перерегулирование и система приближается к границе устойчивости.

Кроме частоты ω_max характерными частотами АЧХ являются частота среза ω_с и полоса пропускания ω_п. Частота среза замкнутой системы ω_с определяется на уровне Δ(ω) = 1.Для следящих систем частота среза определяет диапазон вынужденных колебаний, которые система пропускает без ослабления. На этой частоте амплитуды входного и выходного колебаний равны. Полоса пропускания ω_п замкнутой системы определяется на уровне Δ(0)/√2 = 0,707. Так как в диапазоне частот (ω_с – ω_п) АЧХ резко «падает», то числовые значения частот ω_с и ω_п близки.

Полоса пропускания влияет на точность и быстродействие системы. С увеличением полосы пропускания быстродействие системы растет. Чем больше полоса пропускания, тем больший спектр частот входного сигнала передается без искажений.

О качестве регулирования можно судить по ЛАЧХ. Установлено, что для удовлетворительного качества регулирования участок средних частот, на котором ЛАЧХ пересекает ось абсцисс, должен имеет наклон минус 20 дБ/декаду. Протяженность этого участка влияет на перерегулирование. С его увеличением уменьшается колебательность переходного процесса. Приемлемое качество переходного процесса имеет место, если протяженность этого участка примерно равна декаде. Время регулирования t_p зависит от частоты среза, при которой ЛАЧХ пересекает ось абсцисс. Чем больше частота среза, тем меньше t_p.

Корневые оценки. Корневыми называются оценки, которые основываются на расположении корней характеристического уравнения замкнутой системы, которые являются полюсами передаточной функции замкнутой системы и находятся из уравнения W_з(ω) = ∞.

Корневой оценкой качества является степень устойчивости – расстояние η от мнимой оси до ближайшего корня на плоскости корней характеристического уравнения замкнутой системы.

 

 

Если ближайшим является вещественный корень (схема а), то ему соответствует экспоненциальная составляющая решения для переходного процесса С₁ = ехр(-η∙t) – апериодическая степень устойчивости η. Время ее затухания t_п = 3/η при погрешности 5% характеризует общую длительность переходного процесса, так как все остальные члены решения, соответствующие основным корням затухают быстрее.

Если же ближайшей к мнимой оси окажется пара комплексных сопряженных корней (схема б), то доминирующей составляющей решения для переходного процесса является С₁ = ехр(-η∙t)∙sin(β₁∙t + C₂), которая называется колебательной составляющей – колебательная степень устойчивости η. При этом оценка длительности переходного процесса остается прежней t_п = 3/η.

Колебательность переходного процесса определяется величиной μ = β/η, где β и η – соответственно мнимая и вещественная части корней характеристического уравнения. Эта величина характеризует быстроту затухания колебаний за каждый период. Чем больше величина μ, называемая колебательностью, тем слабее затухания колебаний в переходном процессе.

Для уменьшения амплитуд отклонений в переходном процессе желательно, чтобы нули передаточной функции замкнутой системы W_з(р), представляющие собой значения р, при котором W_з(р) = 0, располагались вблизи ее полюсов.

Понятие о коррекции. Основная задача корректирующих устройств в улучшении точности и качества переходных процессов систем САУ. Кроме того, корректирующие устройства предварительно используются для обеспечения устойчивости неустойчивых систем.

Для уменьшения ошибок в установившемся режиме необходимо повышать коэффициент усиления К системы в разомкнутом состоянии. Но с увеличением К, как мы с вами уже отмечали ранее, уменьшается запас устойчивости САУ. С возрастанием К увеличивается и частота среза ω_с (ω_с2>ω_с1).

 

 

Большим значениям ω_с соответствуют меньшие значения запаса устойчивости по фазе ψ. При ω_с = ω_с2 система неустойчива из-за вносимого инерционными звеньями системы запаздывания колебаний по фазе, которое растет с увеличением частоты.

Для того, чтобы при увеличении К система оставалась устойчивой и обеспечивала требуемый запас устойчивости по фазе ψ и амплитуде h, необходимо частично компенсировать запаздывание в полосе частот, которая расположена около частоты среза ω_с2, соответствующей увеличенному коэффициенту К₂ системы, и тем самым деформировать ЛФЧХ системы, приподняв ее вверх (штриховая кривая). Такую деформацию ЛФЧХ можно осуществить, включив последовательно элементам системы устройство, которое вносило бы опережение по фазе синусоидальных колебаний.

Коррекция САУ осуществляется с использованием последовательных и параллельных корректирующих устройств.

Последовательные корректирующие устройства. К числу последовательных корректирующих устройств относится дифференцирующая фазоопережающая цепь, которая называется форсирующей цепью.

Передаточная функция этой цепи имеет следующий вид:

 

W(p) = U_вых(р)/U_вх(р) = R₂∙(1 + pR₁∙C)/(R₂ + R₁ + pR₁∙R₂∙C) (2)

 

 

Разделим числитель и знаменатель дроби (2) на сумму сопротивлений (R₁ + R₂), в результате получим

 

W(p) = 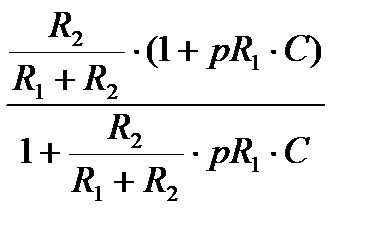. (3)

 

Обозначим отношение R₂/(R₁ + R₂) как K – статический коэффициент усиления, произведение (R₁∙С) как постоянную времени Т₁, а К∙Т₁ = Т₂. Здесь постоянные времени характеризуют соответственно опережение Т₁ и отставание Т₂ (поскольку К< 1, то Т₂< Т₁). Подставив в формулу (3) соответствующие замены, получим стандартное изображение передаточной функции форсирующего звена:

 

W(p) = К∙(1 + р∙Т₁)/(1 + р∙Т₂). (4)

 

ЛАЧХ данного звена имеет вид:

 

L(ω) = 20lgH(ω) = 20lgK + 20lg . (5)

 

ЛФЧХ форсирующегозвена:

 

φ(ω) = arctg(ωТ₁) - arctg(ωТ₂). (6)

 

Примечание: L(ω) = 20lgK в диапазоне частот (0 – 1/Т₁), (20lgK + 20дБ/дек) в диапазоне частот (1/Т₁ - 1/Т₂) и (20lgK + 20дБ) = const в диапазоне частот ω> 1/Т₂. Фазовый уголφ(ω) с ростом частоты до ω_max изменяется от 0^о до +45^о, а затем вновь падает до 0^о.

Опережение создается благодаря тому, что Т₁> Т₂. Частоту ω_max, при которой цепь создает максимальное опережение, находим из условия dφ(ω)/dω = 0: ω_max = 1/ .

Подставляя в формулу (6) выражение для ω_max, определяем значение фазового угла, соответствующее данной частоте:

 

φ(ω) = arctg(Т₁ / ) - arctg(Т₂ / ) = arctg - arctg 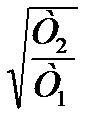. (7)

 

Из формулы (7) следует, что получение больших углов опережения связано с уменьшением коэффициента усиления цепи К. Для компенсации ослабления вносимого фазоопережающей цепью, необходимо увеличивать коэффициент усиления системы другими ее элементами.

Для уменьшения влияния помех САУ целесообразно корректировать, используя интегрирующее устройство, которое позволяет увеличивать К, не повышая ее частоты среза.

Передаточная функция наиболее распространенной пассивной интегрирующей цепи имеет следующий вид:

 

 

W(p) = U_вых(р)/U_вх(р) = (pR₂∙C + 1)/(pR₁∙C + pR₂∙C + 1). (8)

 

Обозначим произведение R₂∙C как _Т2 – постоянная времени опережения контура, С∙(R₁ + R₂) = Т₁ – постоянная времени отставания. Подставив замены в выражение (8), получим:

 

W(p) = (1 + р∙Т₂)/(1 + р∙Т₁). (9)

 

Наличие отставания, вносимого интегрирующим устройством, является недостатком корректирующего устройства. Однако при соответствующем выборе параметров этого устройства область отставания может быть смещена в диапазон низких частот значительно левее частоты среза системы, поэтому запас устойчивости системы при включении интегрирующего звена практически не уменьшается.

ЛАЧХ данного звена имеет вид:

 

L(ω) = 20lgH(ω) = 20lg . (10)

 

ЛФЧХ интегрирующего звена:

 

φ(ω) = arctg(ωТ₂) - arctg(ωТ₁). (11)

 

Примечание: L(ω) = 0 в диапазоне частот (0 – 1/Т₁), (- 20дБ/дек) в диапазоне частот (1/Т₁ - 1/Т₂) и (- 20дБ) = const в диапазоне частот ω> 1/Т₂. Фазовый уголφ(ω) с ростом частоты до ω_max изменяется от 0^о до некоторого отрицательного максимума (больше – 90^о), а затем вновь падает до 0^о.

На практике для коррекции САУ часто применяют интегро-дифференцирующие цепи.

 

Передаточная функция этой цепи имеет вид:

 

W(p) = U_вых(р)/U_вх(р) = (1 + р∙Т₁)∙(1 + р∙Т₂)/[ (1 + р∙Т₃)·(1 + р∙Т₄)], (12)

 

где Т₁ = R₁∙C₁; Т₂ = R₂∙C₂; T₃ + T₄ = R₁∙C₁ + (R₁ + R₂)∙C₂; T₃ · T₄ = T₁ · T₂.

 

ЛФЧХ интегро-дифференцирующего звена:

 

φ(ω) = arctg(ωТ₂) + arctg(ωТ₁) - arctg(ωТ₃) - arctg(ωТ₄). (13)

 

Примечание: L(ω) = 0 в диапазоне частот (0 – 1/Т₃), (- 20дБ/дек) в диапазоне частот (1/Т₃ - 1/Т₁), (- 20дБ) = const в диапазоне частот (1/Т₁ - 1/Т₂), (+ 20дБ/дек) в диапазоне частот (1/Т₂ - 1/Т₄) и 0 в диапазоне частот в диапазоне частот ω> 1/Т₄. Фазовый угол φ(ω) с ростом частоты имеет два максимума: отрицательный более - 90^о и положительный менее 90^о, а также нулевой угол в средней части диапазона частот (1/Т₁ - 1/Т₂).

Используя последовательную интегро-дифференцирующую цепь можно значительно повысить коэффициент усиления системы и увеличить ее частоту среза, а следовательно повысить точность системы в установившемся и переходном режимах.

Параллельные корректирующие устройства. Параллельное корректирующее устройство выполняет функции обратной связи, которая охватывает один из элементов прямой цепи системы.

 

 

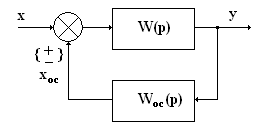
Передаточная функция этой части системы W_охв(р) = W(p)/[1 + W(p)∙W_oc(p)] может быть представлена в следующем виде: W_охв(р) = W(p)∙W_n(p), где W_n(p) = 1/[1 + W(p)∙W_oc(p)] – передаточная функция последовательно включенного звена, эквивалентного параллельному корректирующему устройству с передаточной функцией W_oc(p).

 

Таким образом, если удается повысить показатели качества, используя последовательные корректирующие устройства, то такое же повышение показателей качества можно осуществить и, используя параллельные корректирующие устройства. Если известно W_n(p), то можно найти W_oc(p):

 

W_oc(p) = [1 – Wn(p)]/[W_n(p)∙W(p)]. (14)

 

Если в какой-либо области частот выполняется условие |W(jω)∙W_oc(jω)| >> 1, то

W_охв(jω) = W(jω)/[1 + W(jω)∙W_oc(jω)] ≈ 1/W_oc(jω), (15)

 

т.е. передаточная функция части системы, охваченной обратной связью, в этой области частот полностью определяется передаточной функцией параллельного корректирующего устройства. Благодаря этому применением параллельных корректирующих устройств удается изменить частотные характеристики систем САУ в желаемом направлении.

Корректирующие обратные связи делятся на жесткие и гибкие. Жесткая обратная связь действует на систему в переходном и установившемся режимах, т.е. W_жос(0) ≠ 0, и реализуется она безинерционным (W_жос = К_ос) или инерционным [W_жос(p) = К_ос/(T_ocp + 1)] звеньями.

Гибкая обратная связь действует лишь в переходных режимах. Реализуется она дифференцирующим [W_гос(р) = К_оср] или инерционно-дифференцирующим звеном [W_гос(p) = К_оср/(T_ocp + 1)]. При охвате интегрирующего звена [W_δ(p) = K/p] отрицательной жесткой обратной связью (W_жос = К_ос) получим:

 

W(p) = K/(p + K∙K_oc) = K₁/(T₁p + 1), (16)

 

где К₁ = 1/К_ос: Т₁ = 1/К∙К_ос.

Таким образом, под действием жесткой обратной связи теряется интегрирующее свойство звена и оно превращается в апериодическое с коэффициентом усиления, который полностью определяется только обратной связью. Постоянная времени Т₁ мала при большом коэффициенте усиления звена К.

При охвате инерционного интегрирующего звена гибкой обратной связью:

W(p) = K/[p∙(Tp + 1); W_oc(p) = K_oc∙p;

 

W_охв(р) = K/[p∙(Tp + 1 + K∙K_oc)] = K₁/[p∙(T₁p + 1), (17)

 

где K₁ = К/(1 + К∙К_ос); Т1 = Т/(1 + К∙К_ос).

Т.е. в этом случае сохраняется тот же тип интегрирующего звена, но с уменьшенной инерционностью.