Требования к процессу управления. Системы САУ выполняют задачу стабилизации или управления. В первом случае система поддерживает регулируемую величину на заданном уровне, а во втором – с заданной точностью изменяет регулируемую величину по определенному закону.
Режим работы системы, при котором отклонение регулируемой величины от заданного значения не превышает допустимого, называется установившимся режимом. В общем случае, за установившийся режим принимается такой режим, при котором ошибка системы (разность между заданным и фактическим значением регулируемой величины) постоянна во времени. Установившийся режим часто называют невозмущенным движением системы.
Если на систему действуют возмущающие внешние воздействия, то в системе возникает возмущенное движение, которое называют переходным процессом.
Процесс управления во времени определяется решением уравнения динамики системы:
y(t) = yв(t) + yсв(t), (1)
где yв(t) – вынужденная составляющая, yсв(t) – свободная (переходная) составляющая.
За невозмущенное движение принимается вынужденная составляющая yв(t), представляющая собой установившуюся часть процесса управления. На нее накладывается переходной процесс yсв(t), который теоретически длится бесконечно долго, но его влияние практически становится существенно малым через определенное конечное время. Послезатуханияпереходнойсоставляющейустанавливаетсяyв(t).
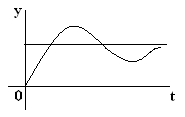
По графику установившегося процесса определяется точность САУ. При этом установившаяся ошибка системы равна:
εус(t) = yв(t) – x(t), (2)
а полное значение ошибки: ε (t) = y(t) – x(t). (3)
С целью обеспечения нормального протекания процесса управления к системе САУ предъявляются требования по точности, устойчивости и качеству переходного процесса.
Точность системы задается и определяется в установившихся режимах. Устойчивость гарантирует затухание переходного процесса, после чего обеспечивается желаемое качество затухающего переходного процесса.
Точность при типовых воздействиях. Значение установившейся ошибки можно найти по теореме операционного исчисления о конечном значении функции. Суть теоремы звучит так: если известно изображение F(p) функции f(t), то конечное значение оригинала f(t → ∞) можно вычислить по формуле:
f(t → ∞) = lim[p∙F(p)] при р → 0.
Применяя эту формулу для решения поставленной задачи, получим:
εус = lim[р∙Wε(p)∙x(p)] при р → 0, (4)
где Wε(p) – передаточная функция, представляющая собой отношение установившейся ошибки εус к входной величине х.
В общем случае задающее воздействие является сложной функцией времени, при которой вычисление ошибки значительно усложняется. Поэтому реальные управляющие воздействия заменяют типовыми, в качестве которых применяют известную вам ступенчатую функцию m∙1(t), линейную функцию а∙t или квадратичную функцию at2/2.
Эти воздействия называются детерминированными или регулярными, поскольку их значения можно вычислить для любого момента времени.
Передаточная функция ошибки замкнутой системы определяется в соответствии с выражением:
Wε(p) = 1/[1 + W(p)], (5)
где W(р) – передаточная функция разомкнутой системы.
Подставляя выражение (5) в уравнение (4), получим:
εус = lim{р∙x(p)/[1 + W(p)]} при р → 0. (4)
Если W(0) = К, т.е. структурная схема разомкнутой системы не содержит интегрирующих звеньев, то САУ называется статической, где К – статический коэффициент усиления разомкнутой системы.
Астатическими системами первого и второго порядка называют такие, у которых передаточные функции соответственно равны W(p) = К·W*(p)/р и W(p) = К·W*(p)/р2, т.е. структурные схемы систем содержат одно или два интегрирующих звена. При этом W*(p) – передаточная функция без учета интегрирующих звеньев и их коэффициентов усиления.
При вычислении ошибок необходимо иметь в виду, что изображение по Лапласу типовых воздействий для х = хо, х = а∙t и х = at2/2 равно соответственно:
х(р) = хо/р; х(р) = а/р2; х(р) = а/р3. (5)
Рассмотрим ошибки некоторых САУ при типовых воздействиях.
Подставив в выражение (4) значение х(р) для ступенчатого воздействия найдем установившуюся ошибку статической системы САУ при р = 0:
εус = р∙x(p)/[1 + W(p)] = p∙ хо/{р∙[1 + W(p)]} =
= хо/[1 + W(p)] = хо/[1 + W(0)] = хо/(1 + K). (6)
Эта ошибка называется статической ошибкой. Она пропорциональна задающему воздействию и уменьшается с увеличением коэффициента К разомкнутой системы. При изменяющихся во времени воздействиях типа х(t) = а∙t или х = at2/2 ошибка непрерывно возрастает и при р → 0 εус → ∞.
εус = а/[p∙(1 + K)]; εус = а/[p2∙(1 + K)]. (7)
Наличие статической ошибки является характерным свойством статических САУ.
Астатические системы первого порядка точно отрабатывают ступенчатое воздействие.
εус = р∙x(p)/[1 + W(p)] = p∙ хо/{р∙[1 + К·W*(p)/p]} =
= хо∙p/[p + К·W*(p)] = 0/[0 + W(0)] = 0/K = 0. (8)
В то же время при отработке линейно возрастающего сигнала эти системы имеют постоянную ошибку εус = а/K:
εус = р∙x(p)/[1 + W(p)] = p∙ а/{р2∙[1 + К·W*(p)/p]} =
= а/[p + К·W*(p)] = а/[0 + W(0)] = а/K. (9)
Эта ошибка пропорциональна скорости изменения входного сигнала «а», поэтому ее называют скоростной ошибкой, а коэффициент усиления разомкнутой системы К – добротностью системы по скорости.
При отработке квадратичного сигнала отклонение εус → ∞.
εус = р∙x(p)/[1 + W(p)] = p∙ а/{р3∙[1 + К·W*(p)/p]} =
= а/{р∙[p + К·W*(p)]}. (10)
Астатические системы второго порядка точно отрабатывают ступенчатый и линейно возрастающие сигналы. При отработке квадратичного сигнала имеет место ошибка εус = а/K, которая пропорциональна ускорению «а» входного сигнала и обратно пропорциональна коэффициенту усиления разомкнутой системы К, который называется добротностью системы по ускорению, а сама ошибка - ошибка системы по ускорению.
С увеличением коэффициента усиления К разомкнутой системы установившиеся ошибки уменьшаются. Однако с возрастанием К ухудшается устойчивость автоматических систем, т.е. требование к точности противоречит требованию к устойчивости. При заданном относительно большом значении К улучшение устойчивости достигается включением в систему корректирующих устройств.
Порядок астатизма системы также влияет на точность системы. Чем выше астатизм, тем точнее система отрабатывает более сложные воздействия. Однако с увеличением порядка астатизма системы ее устойчивость ухудшается. Поэтому системы САУ с порядком астатизма более двух встречаются редко.






