Системы САУ в большинстве случаев являются замкнутыми системами. Однако при их анализе (например, устойчивости) и проектировании часто предварительно рассматривается разомкнутая цепь звеньев, которая затем замыкается.
Различают последовательное, параллельное и параллельное с обратной связью соединение звеньев.


Последовательным соединением звеньев называют такое соединение, когда выходная величина предыдущего звена является входной величиной последующего звена (схема а), т.е. ym-1 = хm.
Передаточная функция разомкнутой цепи n последовательно соединенных звеньев равна произведению передаточных функций всех звеньев:
W(p) = y(p)/x(p) = W1(p)∙W2(p) ∙…∙Wn(p). (1)
Полагая p = jω, перейдем от передаточных функций в операторном виде к частотным характеристикам.
АФЧХ = W(jω) = W1(jω)∙W2(jω) ∙…∙Wn(jω) = H(ω)∙exp[φ(ω)] =
= H1(ω)∙H2(ω) ∙…∙Hn(ω)∙expj[φ1(ω) + φ2(ω) + … + φn(ω)]. (2)
АЧХ = H(ω) = H1(ω)∙H2(ω) ∙…∙Hn(ω). (3)
ФЧХ = φ(ω) = φ1(ω) + φ2(ω) + … + φn(ω). (4)
ЛАЧХ = L(ω) = 20lgH(ω) = 20  . (5)
. (5)
Таким образом, при последовательном соединении звеньев амплитудно-частотные характеристики перемножаются, а логарифмические амплитудно-частотные и фазовые частотные характеристики складываются.
Рассмотрим получение асимптотической ЛАЧХ разомкнутой цепи при последовательном соединении звеньев на следующем примере.
Пусть передаточная функция разомкнутой цепи описывается следующей формулой:
W(p) = 
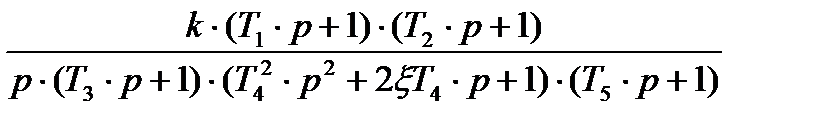 . (6)
. (6)
При этом коэффициент демпфирования ξ принимаем 0,5 <ξ< 1 (при таких значениях ξ можно не учитывать «горб» АЧХ колебательного звена).
Асимптотическую ЛАЧХ можно построить непосредственно по передаточной функции. При этом каждому сомножителю (Тр + 1) в знаменателе соответствует точка излома характеристики при ω = 1/Т с последующим наклоном минус 20 дБ/декаду, а каждому сомножителю такого же типа в числителе соответствует точка излома также при ω = 1/Т, но с последующим наклоном плюс 20дБ/декаду. Сомножителю (Т2р2 + 2ξТр + 1) в знаменателе соответствует излом характеристики при ω = 1/Т с наклоном минус 40 дБ/декаду.
Методика построения асимптотической ЛАЧХ сводится к следующему:
1) определяем сопрягающие частоты типовых звеньев в порядке возрастания. Так, например, дляслучая Т1 > T3 > T4 > T2 > T5:
ω1 = 1/Т1; ω2 = 1/Т3; ω3 = 1/Т4; ω4 = 1/Т2; ω5 = 1/Т5;
2) вычисляем на частоте ω = 1 ординату L(1) = 20lgK, где К – общий коэффициент усиления разомкнутой системы. Через полученную точку проводим низкочастотную асимптоту ЛАЧХ, представляющую собой прямую с наклоном минус 20∙m дБ/декаду, где m – число интегрирующих звеньев (в нашем примере согласно формуле (6) m = 1).
3) изменяем наклон асимптот ЛАЧХ на сопрягающих частотах по отношению с наклоном, который имела ЛАЧХ до рассматриваемой частоты.
Фазовая частотная характеристика определяется по выражению:
φ(ω) = - 90о + arctg(ωT1) + arctg(ωT2) - arctg(ωT3) - arctg  - arctg(ωT5)
- arctg(ωT5)

Параллельным соединением звеньев называется такое соединение, когда на входы всех звеньев подается одна и та же величина, а выходные сигналы суммируются (схема б). Если соединяются n звеньев, то входной сигнал равен: х = х1 = х2 = … хi = … = хn, а выходной сигнал у =  .
.
Переходя к операторной форме представления выходной функции, получим:
y(p) = x(p)∙  ,
,
откуда: W(p) = y(p)/x(p) =  . (7)
. (7)
Таким образом, при параллельном соединении звеньев передаточные функции каждого звена суммируются.
Так как передаточная функция W(p) есть ничто иное, как изображение весовой функции, то весовая функция g(t), а, следовательно, и переходная функция h(t) разомкнутой цепи, состоящей из параллельно соединенных n звеньев, равны сумме соответственно весовых и передаточных функций отдельных звеньев:
g(t) =  ; h(t) =
; h(t) =  . (8)
. (8)
При параллельном соединении звеньев с обратной связью (схема «в» замкнутой системы САУ) обратная связь может быть положительной, если сигнал обратной связи хос складывается с входным сигналом х, или отрицательной, если сигнал обратной связи хос вычитается из х.
При отрицательной обратной связи схема описывается следующим уравнением:
y(p) = W1(p)∙[x(p) – xoc(p)]. (9)
Вместе с тем сигнал обратной связи хос определяется в соответствии с выражением:
xoc(p) = W2(p)∙y(p). (10)
Подставляя значение хос из формулы (10) в уравнение (9), получим:
y(p) = W1(p)∙[x(p) – W2(p)∙y(p)] (11)
Решим уравнение (11) относительно y(p):
y(p)∙[1 + W1(p)∙W2(p)] = W1(p)∙x(p). (12)
Отсюда:
у(р) = W1(p)∙x(p)/[1 + W1(p)∙W2(p)] = Wз(p)∙x(p). (13)
Передаточная функция замкнутой системы при отрицательной обратной связи Wз(p) определяется в соответствии с выражением (13):
Wз(p) = у(р)/х(р) = W1(p)/[1 + W1(p)∙W2(p)] (14)
При положительной обратной связи:
Wз(p) = у(р)/х(р) = W1(p)/[1 - W1(p)∙W2(p)] (14)






