Математическая модель ИС была представлена на рис. 3.1,б.
Первая часть модели, содержащая так называемое уравнение преобразования, имеет вид (3.8):
y=F(х  ,..., x
,..., x  , x
, x 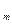 , Т, a
, Т, a  ,..., ak, z). (3.79)
,..., ak, z). (3.79)
Аргументы оператора F являются воздействующими величинами, случайными переменными либо случайными нестационарными процессами, а уравнение преобразования имеет стохастический характер.
Вторая часть модели представляет собой процедуру градуировки (3.5):
x* = φ (y) = F  (y), (3.80)
(y), (3.80)
где
F  = F
= F  (х
(х  ,..., x
,..., x  , x
, x 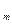 , a
, a  ,..., a
,..., a  ), (3.81)
), (3.81)
т. е. является функцией номинальных (постоянных или детерминированных) значений конструктивных параметров, а также измеряемых входных величин.
Погрешность ИС определяется по (3.7) как разность значения измеряемой величины, восстановленной на основе показаний ИС, и собственно измеряемой величины:
∆ = x* - х,(3.82)
т. е.
∆ = φ [F(х  ,..., x
,..., x  , x, T, a
, x, T, a  ,..., ak, z)] - x =
,..., ak, z)] - x =
= F  [F(х
[F(х  ,..., x
,..., x  , x, T, a
, x, T, a  ,..., ak, z)] – x. (3.83)
,..., ak, z)] – x. (3.83)
В наилучшем случае, когда F = F0, вычитаемое в формуле погрешности не равно х ввиду различия аргументов операторов F0 и F: аргументами F0 служат детерминированные величины, а аргументами F — случайные величины.
Воспользуемся примером. Уравнение преобразования магнитоэлектрического прибора имеет вид:
α = Φ zl·J / D = 




 ·x/
·x/ 
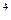 =
=  x, (3.84)
x, (3.84)
где х=1, у = a, a  = Φ, a 2 = z, a
= Φ, a 2 = z, a  = l, a4 = D. Конструктивные параметры могут быть случайными величинами, что обозначено тильдой над буквой.
= l, a4 = D. Конструктивные параметры могут быть случайными величинами, что обозначено тильдой над буквой.
Процедура градуировки описывается соотношением
x* = φ (α) = cα = α/k  , (3.85)
, (3.85)
где c = const (обычно c = l/k  ). Отсюда получаем
). Отсюда получаем
∆ = x* - x = ( /k
/k  )x – x = (
)x – x = ( /k
/k  - 1)x = (
- 1)x = ( - k
- k  )x/k
)x/k  . (3.86)
. (3.86)
Здесь  /k0 ≠ 1, так как
/k0 ≠ 1, так как  — случайная величина. Отметим, что ∆, как и у, является функцией источников погрешностей a
— случайная величина. Отметим, что ∆, как и у, является функцией источников погрешностей a  (j = 1,..., k), которые представляют собой нестационарные случайные процессы; поэтому ∆, как функция a
(j = 1,..., k), которые представляют собой нестационарные случайные процессы; поэтому ∆, как функция a  , тоже является нестационарным случайным процессом. Интерпретация свойств конструктивного параметра, представленная на рис. 3.14, учитывает внутреннюю изменяемость a
, тоже является нестационарным случайным процессом. Интерпретация свойств конструктивного параметра, представленная на рис. 3.14, учитывает внутреннюю изменяемость a  , выраженную составляющей ∆
, выраженную составляющей ∆ 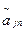 , зависящей от времени, а также внешнее влияние условий использования ИС, выраженное влияющими величинами. Следовательно, погрешность ∆ представляет собой многомерный случайный процесс, а ее аргументами являются входные величины х
, зависящей от времени, а также внешнее влияние условий использования ИС, выраженное влияющими величинами. Следовательно, погрешность ∆ представляет собой многомерный случайный процесс, а ее аргументами являются входные величины х 
 , а также время Т эксплуатации ИС, т. е.
, а также время Т эксплуатации ИС, т. е.
{  } = {
} = { 
 (x
(x  ,..., x
,..., x 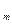 , T)}. (3.87)
, T)}. (3.87)
Здесь индекс k — порядковый номер реализации процесса. Реализации процесса {  } происходят в действительном времени t
} происходят в действительном времени t  T
T  T. Физический смысл погрешности как случайного процесса состоит в том, что ИС размещается в m +1-мерном случайном поле с координатами x
T. Физический смысл погрешности как случайного процесса состоит в том, что ИС размещается в m +1-мерном случайном поле с координатами x  ,..., x
,..., x  (где xm+1 = T). В зависимости от положения ИС в этом поле получаются различные реализации погрешностей. Так, например, если x
(где xm+1 = T). В зависимости от положения ИС в этом поле получаются различные реализации погрешностей. Так, например, если x  = xio= = const, i= l ,..., т — 1, T = const, то процесс возникновения погрешности одномерен, {
= xio= = const, i= l ,..., т — 1, T = const, то процесс возникновения погрешности одномерен, {  }={
}={  (x)}. На рис. 3.15 представлены распределения погрешностей электроизмерительных показывающих приборов — магнитоэлектрического и электромагнитного, причем электромагнитный прибор имеет квадратичную характеристику y = ax2.
(x)}. На рис. 3.15 представлены распределения погрешностей электроизмерительных показывающих приборов — магнитоэлектрического и электромагнитного, причем электромагнитный прибор имеет квадратичную характеристику y = ax2.
Магнитоэлектрический прибор характеризуется нормальным распределением погрешностей с постоянной дисперсией σ2= const для данного х, а среднее значение погрешности E  {
{  k } = m (x)зависит от значения х, что отмечено на рисунке ломаной линией. Распределение погрешностей электромагнитного прибора характеризуется тем, что среднее значение погрешности т (х) и дисперсия σ 2 (х)зависят от аргумента х.
k } = m (x)зависит от значения х, что отмечено на рисунке ломаной линией. Распределение погрешностей электромагнитного прибора характеризуется тем, что среднее значение погрешности т (х) и дисперсия σ 2 (х)зависят от аргумента х.
Могут существовать как частные случаи ИС с погрешностями, описываемыми стационарными процессами. Так, например, магнитоэлектрический измерительный прибор может иметь пренебрежимо малую систематическую погрешность и случайную погрешность с постоянной дисперсией, что позволяет описать эти свойства стационарным процессом в данных условиях сравнения.
Во многих случаях нестационарный процесс погрешностей {  } можно представить с помощью стационарного процесса {ε} и функций h(x
} можно представить с помощью стационарного процесса {ε} и функций h(x 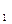 ,..., xm, Т), g(x
,..., xm, Т), g(x 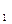 ,..., xm, Т) измеряемых аргументов, таких что
,..., xm, Т) измеряемых аргументов, таких что
{  } = g(x
} = g(x 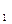 ,..., xm, T){ ε }+ h(x
,..., xm, T){ ε }+ h(x 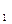 ,..., xm, T). (3.88)
,..., xm, T). (3.88)
Случайный процесс {ε} имеет следующие свойства:
E{ ε } = 0, E{ ε  ² } = 1, (3.89)
² } = 1, (3.89)
E [{ ε  {ε
{ε  }] = E [{ ε
}] = E [{ ε  }{ε
}{ε 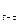 }] = ρ(
}] = ρ( ). (3.90)
). (3.90)
Из приведенного выше следует, что
 {
{  k } =
k } =  [ g (·){ε} + h (·)] = g (·)
[ g (·){ε} + h (·)] = g (·)  {ε} + h (·) = h (x
{ε} + h (·) = h (x 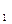 ,..., xm, T), (3.91)
,..., xm, T), (3.91)
а также
var{  k } =
k } =  [({
[({  k } -
k } -  {
{  k })²] = g ²(·)
k })²] = g ²(·)  [{ε }²] = g ²(x
[{ε }²] = g ²(x 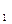 ,..., xm, T), (3.92)
,..., xm, T), (3.92)
если очередные реализации происходят на интервалах времени, больших чем tнач, а ρ(t) = 0 по истечении некоторого времени. Математические ожидания рассчитываются по множеству реализаций.
Без существенных затруднений функцию g, а также h можно определить теоретически или экспериментально. Так, например, в магнитоэлектрическом измерительном приборе неточная балансировка измерительного органа приводит к появлению момента, пропорционального массе этого органа m, ускорению свободного падения g, расстоянию R между центром массы и осью вращения измерительного органа, а также синусам соответствующих углов φ  , β (рис. 3.16), а именно:
, β (рис. 3.16), а именно:
M  = mgR sinβ sin(φ + φ
= mgR sinβ sin(φ + φ  ). (3.93)
). (3.93)
Уравнение моментов  = 0 позволяет получить модель измерительного прибора:
= 0 позволяет получить модель измерительного прибора:
α =  (φ - φ
(φ - φ  ). (3.94a)
). (3.94a)
Здесь I — сила тока,  — чувствительность, b = mgR sinβ /D = const, φ — угловое положение измерительного органа, соответствующее отклонению α. Значения R, φ
— чувствительность, b = mgR sinβ /D = const, φ — угловое положение измерительного органа, соответствующее отклонению α. Значения R, φ  в данном приборе реализованы случайным образом; при этом R
в данном приборе реализованы случайным образом; при этом R 
 , φ
, φ 

 . Если процедура градуировки имеет вид (3.85)
. Если процедура градуировки имеет вид (3.85)
J* = c α и c = 1/ k  ,
,
то
∆= J*-J=c [  J–b sin(φ+ φ
J–b sin(φ+ φ  )] -J =[(
)] -J =[( -k
-k  )/ k
)/ k  ]–(b / k
]–(b / k  )(φ+ φ
)(φ+ φ  ) (3.94б)
) (3.94б)
в интервале φ = φ  = φ
= φ  - φ
- φ  , обусловленном диапазоном измерений. Из определений (3.91), (3.92) и уравнения (3.94б) получаем
, обусловленном диапазоном измерений. Из определений (3.91), (3.92) и уравнения (3.94б) получаем
h (x) = -  sin (φ + φ
sin (φ + φ  ) = -
) = -  sin (k
sin (k  J+ φ
J+ φ  ), (3.94в)
), (3.94в)
поскольку φ = k  J в идеальной модели, а также
J в идеальной модели, а также
g² = var  =
=  , (3.94г)
, (3.94г)
если k0, I = const, а  — случайная переменная со средним значением k0 и дисперсией
— случайная переменная со средним значением k0 и дисперсией 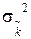 . Процедуру градуировки (3.85) можно подобрать так (например, c = c
. Процедуру градуировки (3.85) можно подобрать так (например, c = c  ≠ 1/ k), чтобы уменьшить систематическую погрешность.
≠ 1/ k), чтобы уменьшить систематическую погрешность.



Рис. 3.16. Определение величин, характеризующих момент, обусловленный неточной балансировкой измерительного органа показывающего прибора:
a — конструктивная схема измерительного органа; б — вид с направления оси 0 ‑ 0 — нулевое положение измерительного органа; R—R — плоскость, проходящая через ось и центр массы; φ  — угол положения этой плоскости; В-В — плоскость отклонения измерительного органа от вертикали; φ
— угол положения этой плоскости; В-В — плоскость отклонения измерительного органа от вертикали; φ  — угол положения этой плоскости; β — угол отклонения измерительного органа от вертикали; R sin γ — плечо силы, вызывающей поворот; mg sinβ — составляющая силы тяжести, поворачивающая измерительный орган
— угол положения этой плоскости; β — угол отклонения измерительного органа от вертикали; R sin γ — плечо силы, вызывающей поворот; mg sinβ — составляющая силы тяжести, поворачивающая измерительный орган
В некоторых случаях модель возникновения погрешности можно построить теоретически. Так, источником погрешности в резисторе может быть тепловой шум, описываемый формулой Найквиста (3.52). Тогда g (θ) попросту равняется  и зависит от температуры θ резистора. Диодный шум имеет дисперсию σ u 2 = 3000 мкВ2.
и зависит от температуры θ резистора. Диодный шум имеет дисперсию σ u 2 = 3000 мкВ2.
Экспериментально определить функции g и h сложнее. Во-первых, для определения g хотя бы в одной точке необходимо такое количество реализаций, чтобы смещение оценки дисперсии было пренебрежимо мало. Пусть это будет число п. То свойство ИС, что g = const, существенно уменьшает необходимое количество измерений. Во-вторых, реализация каждого из аргументов в q точках дает необходимое количество точек:
N = (m + 1)  . (3.95)
. (3.95)
Соответствующий подбор точек влияет на стоимость исследований. Для некоторых измерений, например физико-химических, приходится использовать расходуемые образцы; измерения при переменных температурах требуют много времени. Поэтому необходимы упрощения.






