Дисперсионный анализ разработан и введен в практику сельскохозяйственных и биологических исследований английским ученым Р. А. Фишером, который открыл закон распределения отношения средних квадратов (дисперсий).
Дисперсионный анализ широко используется для планирования эксперимента и статистической обработки его данных. Если в недалеком прошлом считали, что роль математика состоит лишь в анализе экспериментальных данных, то работы Р. А. Фишера коренным образом изменили эту точку зрения, и в настоящее время статистическое планирование опыта в соответствии с требованиями дисперсионного анализа и математическая интерпретация результатов: непременные условия успешного получения ответов на вопросы, интересующие экспериментатора. Статистически обоснованный план эксперимента определяет и метод математического анализа результатов. Поэтому современный эксперимент нельзя правильно спланировать, не зная основ дисперсионного анализа.
При дисперсионном анализе одновременно обрабатывают данные нескольких выборок (вариантов), составляющих единый статистический комплекс, оформленный в виде специальной рабочей таблицы. Структура статистического комплекса и его последующий анализ определяются схемой и методикой эксперимента.
Сущностью дисперсионного анализа является расчленение общей суммы квадратов отклонений и общего числа степеней свободы на части – компоненты, соответствующие структуре эксперимента, и оценка значимости действия и взаимодействия изучаемых факторов по F–критерию.
Если обрабатывают однофакторные статистические комплексы, состоящие из нескольких независимых выборок, например
l –вариантов в вегетационном опыте, то общая изменчивость результативного признака, измеряемая общей суммой квадратов СY, расчленяется на два компонента: варьирование между выборками (вариантами) СV и внутри выборок Cz, Следовательно, в общей форме изменчивость признака может быть представлена выражением:
(14.1)
Здесь вариация между выборками (вариантами) представляет ту часть общей дисперсии, которая обусловлена действием изучаемых факторов, а дисперсия внутри выборок характеризует случайное варьирование изучаемого признака, т. е. ошибку эксперимента.
Общее число степеней свободы (N – 1) также расчленяется на две части – степени свободы для вариантов (l – 1) и для случайного варьирования (N – l);
Суммы квадратов отклонений по данным эксперимента – статистического комплекса с l -вариантами – обычно находят в такой последовательности. При общем числе наблюдений N определяются суммы по вариантам V и общая сумма всех наблюдений ΣХ. Затем вычисляются:
1 корректирующий фактор (поправка) 
(14.2)
2 общая сумма квадратов 
(14.3)
3 сумму квадратов для вариантов 
(14.4)
4 сумму квадратов для ошибки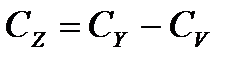 
(14.5)
Две последние суммы квадратов СY и CZ делятся на соответствующие им степени свободы, т. е. приводятся к сравниваемому виду – одной степени свободы вариации. В результате получают два средних квадрата:
вариантов 
(14.6)
и ошибки 
(14.7)
Эти средние квадраты и используют в дисперсионном анализе для оценки значимости действия изучаемых факторов. Оценка проводится путем сравнения дисперсии вариантов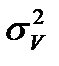 
с дисперсией ошибки 
по критерию Фишера:
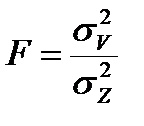. (14.8)
Таким образом, за базу – единицу сравнения принимают средний квадрат случайной дисперсии, которая определяет случайную ошибку эксперимента. При этом проверяемой нулевой гипотезой служит предположение: все выборочные средние являются оценками одной генеральной средней и, следовательно, различия между ними несущественны. Если Fфакт < Fтеop, то нулевая гипотеза Но: d = 0 не отвергается; между всеми выборочными средними нет существенных различий и на этом проверка заканчивается. Нулевая гипотеза отвергается, когда Fфакт ≥ Fтеop.
В этом случае дополнительно проводят оценку, между какими средними имеются значимые различия.
Теоретическое значение критерия F для принятого в исследовании уровня значимости находят по таблицам приложений с учетом числа степеней свободы для дисперсии вариантов и случайной дисперсии. В большинстве случаев избирают 5%–ный, а при более строгом подходе 1%–ный или даже 0,1%–ный уровень значимости.
Вопросы для самоконтроля
1 Сущность дисперсионного анализа.
2 Для каких целей используется дисперсионный анализ?
3 Дайте определения терминам, используемые в дисперсионном анализе: результативный признак, фактор и его градации, градации комплекса, дисперсионный комплекс, факториальное, случайное и общее влияние.
4 В чем заключается принцип дисперсионного анализа?
5 В чем заключается разница факториального и случайного влияний?
6 При каких условиях факториальному влиянию приписывается большая достоверность?
7 На сколько компонентов расчленяется общая сумма квадратов в однофакторном комплексе? Назовите их.
8 Расчленяется ли общее число степеней свободы в однофакторном комплексе?
9 Напишите последовательность проведения расчетов в однофакторном комплексе.
10 Какой критерий используется для оценки значимости действия изучаемых факторов? Напишите формулу этого критерия.
11 Сформулируйте условия, при которых нулевая гипотеза (Н0) подтверждается или отвергается.
ТЕМА 15 Многофакторный дисперсионный анализ
15.3 Многофакторный дисперсионный анализ
15.4 Преобразования
15.5 Универсальное использование дисперсий
