Частный коэффициент корреляции – это показатель, измеряющий степень сопряженности двух признаков при постоянном значении третьего.
Математическая статистика позволяет установить корреляцию между двумя признаками при постоянном значении третьего, не ставя специального эксперимента, а используя парные коэффициенты корреляции rxy, rxz и ryz. Частные коэффициенты корреляции рассчитывают по формулам:
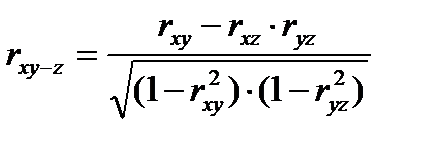; (12.1)
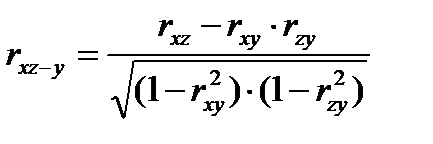; (12.2)
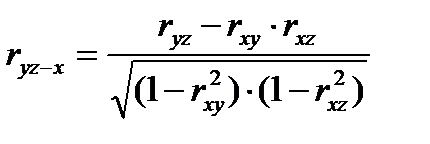. (12.3)
Здесь в индексах буквы перед тире указывают, между какими признаками изучается зависимость, а буква после тире – влияние какого признака исключается (элиминируется). Ошибку и критерий значимости частной корреляции определяют по тем же формулам, что и парной корреляции (11.8):
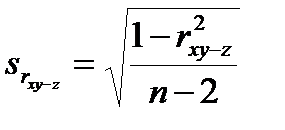; (12.4)
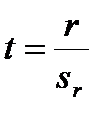(12.5)
Теоретические значения t берут из таблицы приложения критерия Стьюдента для принятого уровня значимости и n–3 степеней свободы.
Подобно парным коэффициентам корреляции частные коэффициенты могут принимать значения, заключенные между –1 и +1. Частные коэффициенты детерминации находят путем возведения в квадрат частных коэффициентов корреляции.
Определение степени частного воздействия отдельных переменных на результативный признак при исключении (элиминировании) связи его с другими признаками, искажающими эту корреляцию, часто представляет большой интерес. Например, тесноту связи урожаев с осадками может сильно искажать варьирование температуры, и поэтому целесообразно изучить связь между первыми двумя признаками при постоянных значениях третьего. С чисто внешней стороны (а не внутренней) при постоянном значении элиминируемого признака нельзя подметить его статистического влияния на изменчивость других признаков: он удерживается на постоянном уровне, а другие признаки варьируют и находятся в корреляционном отношении друг с другом.
Чтобы уяснить технику расчета и смысл частного коэффициента корреляции, рассмотрим данные по определению парной корреляции между окружностями початка кукурузы (X), окружностью его стержня (Y) и количеством рядков зерен (Z) на основании измерения 9000 початков:
rxy = 0,799; rxz = 0,570; ryz = 0,507.
По приведенным выше соотношениям 12.1 – 12.3 определим частные коэффициенты корреляции:
;
;
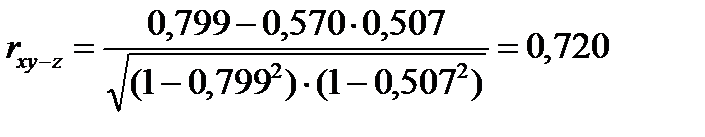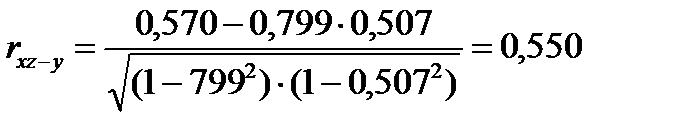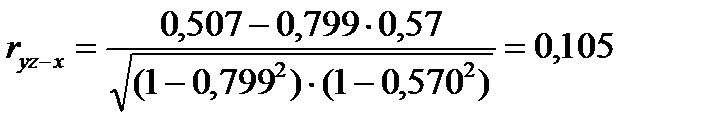
Частный коэффициент корреляции между окружностью початка и его стержня у початков с одинаковым числом рядков зерен
(rxy-z =0,720) показывает, что лишь незначительная часть взаимосвязи этих признаков в общей корреляции (rxy =0,799) обусловлена влиянием третьего признака. Аналогичное заключение необходимо сделать и в отношении частного коэффициента корреляции между окружностью початка и количеством рядков зерен у початков с одинаковой окружностью стержня (rxz-y = 0,55 и rxz = 0,57). Напротив, частный коэффициент корреляции между окружностью стержня и количеством рядков зерен у початков с одинаковой окружностью
ryz-x = 0,105 значительно отличается от общего коэффициента корреляции ryz = 0,507. Из этого видно, что если подобрать початки с одинаковой окружностью, то связь между этими признаками у них будет очень слабой, так как значительная часть в этой взаимосвязи обусловлена варьированием окружности початка.
При некоторых обстоятельствах частный коэффициент корреляции может оказаться противоположным по знаку парному. Например, при изучении взаимосвязи между морфологическими признаками стеблей льна массой (X), длиной (Y) и диаметром (Z) – были получены следующие коэффициенты (n = 100): между массой и длиной rxy = 0,6; между массой и диаметром rxz = 0,9; между длиной и диаметром ryz = 0,4.
Частные коэффициенты корреляции при исключении влияния третьего признака:
;
;
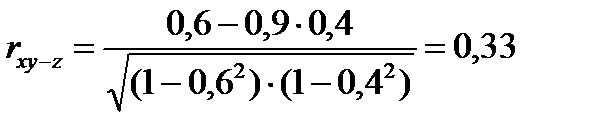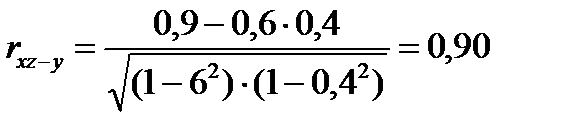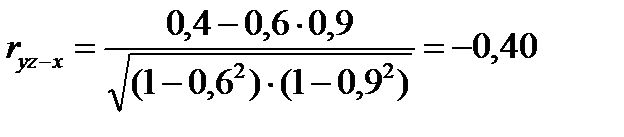
Частные коэффициенты корреляции между массой и длиной и массой и диаметром при статистическом исключении влияния третьего признака не вызывают никаких недоумений. Выявилась очень высокая частная корреляция массы и диаметра при исключении влияния длины стебля rxz-y и слабая корреляция между массой и длиной rx-yz для растений с одинаковым диаметром. Частная корреляция между длиной стебля при постоянном значении массы получилась отрицательной: при увеличении длины диаметр стебля уменьшается, тогда, как общий коэффициент корреляции указывает на положительную взаимосвязь между этими признаками. На первый взгляд этот результат кажется невероятным, он противоречит обычным представлениям о росте растений: если увеличивается высота, то, конечно, увеличивается и диаметр стебля. Однако это мнимое противоречие объясняется основным условием частной корреляции – постоянством исключаемого признака. Если взять стебли льна одной и той же массы, то среди таких стеблей увеличение длины может происходить только за счет уменьшения диаметра. При увеличении обоих признаков не могла бы оставаться постоянной масса стебля.
