Математическое уравнение для прямолинейной зависимости между тремя переменными называется множественным линейным уравнением плоскости регрессии. Оно имеет следующий общий вид:
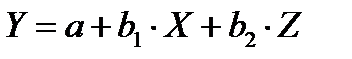 (12.10)
(12.10)
Здесь Y – зависимая переменная, X и Z – независимые переменные, а – общее начало отсчета, b1 и b2 – коэффициенты частной регрессии. Коэффициент b1 показывает, на какую величину увеличивается Y при каждом увеличении на одну единицу X при постоянном значении Z; коэффициент b2 указывает, на какую величину увеличивается Y при увеличении Z на единицу при постоянном значении X. Поэтому часто используют обозначения
b1 = byx-z и b2 = byz-x, принятые для частных коэффициентов корреляции.
Параметры а, b1 и b2 вычисляют методом наименьших квадратов, который позволяет найти такое положение плоскости регрессии в пространстве, когда сумма квадратов отклонений эмпирических точек от нее является минимальной:
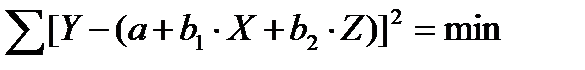 (12.11)
(12.11)
Установленное уравнением регрессии отношение зависимости коррелируемых признаков принято изображать графически в виде линий и поверхности регрессии. Поверхность регрессии дает четкое представление об эффекте комбинированного влияния изучаемых факторов на результативный признак.
Необходимо подчеркнуть, что математические уравнения для парной и множественной регрессии имеют смысл только в области фактических значений X, Y и Z только тогда, когда корреляционная связь значимо отличается от нуля.
Вопросы для самоконтроля
1 Что такое множественная корреляция?
2 Дайте определение частному коэффициенту корреляции.
3 С какими статистическими характеристиками формально связан частный коэффициент корреляции?
4 Дайте определение ошибке и критерию значимости частной корреляции. Отличен ли он от ошибки и критерия значимости парной корреляции?
5 Какие могут принимать значения частные коэффициенты корреляции?
6 Дайте определение множественному коэффициенту корреляции.
7 С какими статистическими характеристиками формально связан множественный коэффициент корреляции?
8 В каких пределах находятся значения множественного коэффициента корреляции?
9 Дайте определение коэффициента множественной детерминации.
10 По какому критерию оценивается значимость множественной корреляции?
11 Напишите линейное уравнение множественной регрессии.
12 Дайте графическую интерпретацию уравнения множественной регрессии.
ТЕМА 13 Криволинейная корреляция и регрессия
13.1 Корреляционное отношение
13.2 Свойства корреляционного отношения
13.3 Ошибка репрезентативности корреляционного отношения
13.4 Критерий линейности корреляции
Корреляционное отношение
Если связь между изучаемыми явлениями существенно отклоняется от линейной, что легко установить по графику, то коэффициент корреляции непригоден в качестве меры связи. Он может указать на отсутствие сопряженности там, где налицо сильная криволинейная зависимость. Поэтому необходим новый показатель, который правильно измерял бы степень криволинейной зависимости. Таким показателем является корреляционное отношение, обозначаемое греческой буквой η (эта). Оно измеряет степень корреляции при любой ее форме.
Корреляционное отношение при малом числе наблюдений вычисляют по формуле:
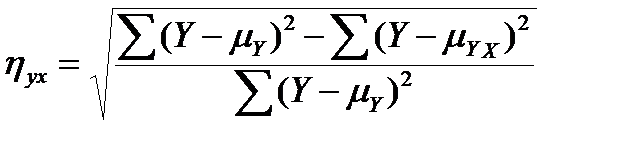 (13.1)
(13.1)
где:
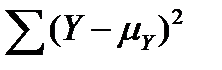 – сумма квадратов отклонений индивидуальных значений Y от общей средней арифметической μY;
– сумма квадратов отклонений индивидуальных значений Y от общей средней арифметической μY;
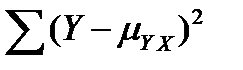 – сумма квадратов отклонений вариант от групповых средних
– сумма квадратов отклонений вариант от групповых средних 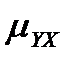 , соответствующих определенным, фиксированным значениям независимой переменной X.
, соответствующих определенным, фиксированным значениям независимой переменной X.
Для вычисления корреляционного отношения значения независимого признака X располагают по ранжиру в возрастающем порядке и разбивают весь ряд наблюдений на 4–7 групп с таким расчетом, чтобы в каждой группе по ряду X было не менее двух наблюдений. Затем определяют общую среднюю μY, групповые средние 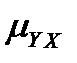 , соответствующие каждой фиксированной группе X, и суммы квадратов отклонений для общего
, соответствующие каждой фиксированной группе X, и суммы квадратов отклонений для общего 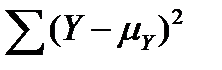 и группового
и группового 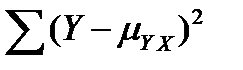 варьирования признака Y.
варьирования признака Y.
При большом объеме наблюдений (n > 30) определяется сумма квадратов отклонений группового варьирования 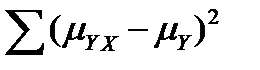 , сумма квадратов отклонений общего варьирования
, сумма квадратов отклонений общего варьирования 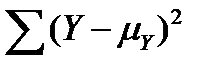 и вычисляется корреляционное отношение по формуле:
и вычисляется корреляционное отношение по формуле:
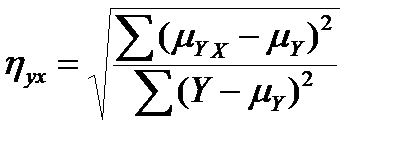 (13.2)
(13.2)
Сумма квадратов отклонений групповых средних 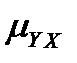 от общей средней μY (групповое варьирование) характеризует ту часть варьирования признака Y, которая связана с изменчивостью признака X. Сумма квадратов разностей между каждой величиной и общей средней μY, т. е.
от общей средней μY (групповое варьирование) характеризует ту часть варьирования признака Y, которая связана с изменчивостью признака X. Сумма квадратов разностей между каждой величиной и общей средней μY, т. е. 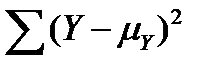 , характеризует общее варьирование признака Y.
, характеризует общее варьирование признака Y.
При функциональной зависимости Y от X корреляционное отношение равно единице; если оно равно нулю, то показывает некоррелированность Y от X; при промежуточном характере корреляционной зависимости корреляционное отношение заключено в пределах: 0 < ηyx < 1.
Чем ближе к единице, тем сильнее функциональная зависимость Y от X, и, наоборот, чем ближе ηyx к нулю, тем слабее выражена эта зависимость.
Отношение сумм квадратов группового варьирования к общему,
т.е. 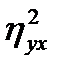 , имеет самостоятельное значение. Оно показывает ту долю варьирования признака Y, которая обусловлена степенью вариаций признака X. Эта величина, называемая коэффициентом детерминации, определяет долю вариации Y под влиянием X.
, имеет самостоятельное значение. Оно показывает ту долю варьирования признака Y, которая обусловлена степенью вариаций признака X. Эта величина, называемая коэффициентом детерминации, определяет долю вариации Y под влиянием X.
Корреляционное отношение измеряет степень криволинейных и прямолинейных связей.
Криволинейная связь между признаками – это такая связь, при которой равномерным изменениям первого признака соответствуют неравномерные изменения второго, причем эта неравномерность имеет определенный закономерный характер.
При графическом изображении криволинейных связей, когда по оси абсцисс откладывают значения первого признака, а по оси ординат – значения второго признака и полученные точки соединяют, получают изогнутые линии. Характер изогнутости зависит от природы коррелируемых признаков.
По виду линии на графике можно определить характер связи (прямолинейная или криволинейная).
Степень статистической зависимости одного признака от другого можно определить, сопоставляя разнообразие этих признаков.
В тех случаях, когда первый признак принимает разные значения, а второй признак остается неизменным, можно заключить, что разнообразие второго признака не зависит от разнообразия первого и связь между ними равна нулю.
Если при значительном разнообразии первого признака второй имеет незначительное разнообразие, можно заключить, что статистическая связь между разнообразием обоих признаков имеется, но она небольшая.
В тех случаях, когда при изменениях первого признака второй признак изменяется часто и значительно, можно сделать вывод о большой связи изменений обоих признаков.
Поэтому для получения показателя криволинейной связи можно определить численно степень разнообразия второго признака при определенном разнообразии первого. Делается это при помощи ряда частных средних, рассчитанных для второго признака при разных значениях первого. Обозначаются частные средние второго признака по первому символом μ2-1. Получение таких средних можно показать на следующем простом примере.
Имеется группа из 6 особей, у каждой особи измерено два признака (первый и второй). В результате получены следующие два ряда значений:
X1 4 4 6 6 8 8
X2 8 4 14 18 4 12.
Как видно, особи по первому признаку могут быть разбиты на группы с одинаковым значением этого первого признака (4, 6 и 8). В каждой такой группе будет по 2 особи.
У первых двух особей первый признак имеет одинаковое значение, второй признак у них неодинаков: у одной особи он равен 8, у другой: 4.
Если взять среднюю из этих значений, то это и будет частная средняя второго признака при определенном значении первого:
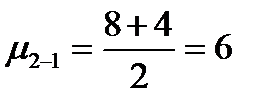
Вторые две особи с одинаковым значением первого признака (6) имеют неодинаковый второй признак (14 и 18). В этом случае частная средняя:
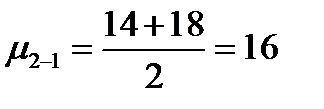
И, наконец, две особи третьей группы имеют одинаковое значение первого признака – 8, второй признак у одной особи равен 4, а у другой: 12. В данном случае частная средняя второго признака по первому:
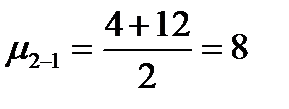
Теперь к имеющимся двумя рядам можно приписать третий
ряд – ряд частных средних второго признака по первому:
X1 4 4 6 6 8 8
X2 8 4 14 18 4 12
μ2-1 6 6 16 16 8 8.
Простое сопоставление полученного ряда частных средних второго признака с рядом первого признака показывает, что второй признак не остается неизмененным при изменениях первого.
При изменении первого признака на одну и ту же величину (2) второй признак сначала резко увеличивается с 6 до 16, а потом столь же резко уменьшается с 16 до 8. При не очень большом разнообразии первого признака (от 4 до 8) разнообразие второго, судя по разнообразию частных средних, получилось довольно значительным: от 6 до 16, что, конечно, указывает на большую связь второго признака с первым, или на большую зависимость второго признака от первого.
Степень разнообразия частных средних можно выразить не только лимитами, но и более точным показателем – суммой квадратов центральных отклонений, или дисперсией. Для получения дисперсии надо рассчитать общую среднюю для всех частных средних второго признака μ2, затем для каждой из них определить центральное отклонение D2-1 = μ2-1 – μ2, полученные величины возвести в квадрат и результат сложить:
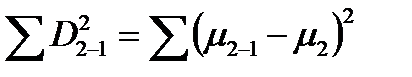 (13.3)
(13.3)
В разбираемом примере этот расчет показан в последних нескольких строках таблицы 13.1.
Сумма центральных отклонений для ряда частных средних второго признака по первому 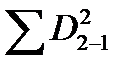 = 112. Это – величина именованная и поэтому имеет значение только для небольшой группы, которая доступна изучению.
= 112. Это – величина именованная и поэтому имеет значение только для небольшой группы, которая доступна изучению.
Таблица 13.1 – Расчет дисперсий
| X1 | 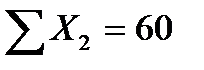
| ||||||
| X2 | μ2 = 60/6 = 10 | ||||||
| μ2-1 | |||||||
| D2-1=(μ2-1 – μ2) | –4 | –4 | +6 | +6 | –2 | –2 | |
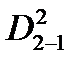 =(μ2-1 – μ2)2 =(μ2-1 – μ2)2
| 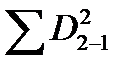 =112 =112
| ||||||
| D2=(X2 – μ 2) | –2 | –6 | +4 | +8 | –6 | +2 | |
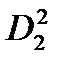 =(X2 – μ2)2 =(X2 – μ2)2
| 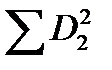 =160 =160
|
Чтобы выяснить, насколько велика эта величина, необходимо отнести ее к сумме центральных отклонений по всему второму признаку 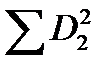 , которая рассчитывается обычным путем по разностям между каждым значением признака и общей средней изучаемого признака
, которая рассчитывается обычным путем по разностям между каждым значением признака и общей средней изучаемого признака 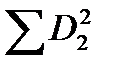 =160.
=160.
Это значит, что степень разнообразия второго признака, связанная с изменчивостью всех факторов, влияющих на его развитие, выражается для разбираемого примера числом 160.
Разнообразие этого же признака, происшедшее в связи с тем, что первый признак принимал различные, постепенно увеличивающиеся значения, выражается меньшим числом 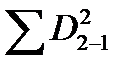 = 112. Отношение этих двух показателей – частного и общего разнообразия – есть квадрат корреляционного отношения второго признака по первому:
= 112. Отношение этих двух показателей – частного и общего разнообразия – есть квадрат корреляционного отношения второго признака по первому:
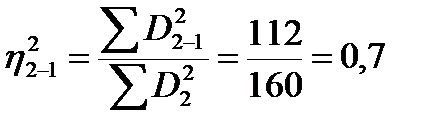 . (13.4)
. (13.4)
Корреляционное отношение второго признака по первому для рассматриваемого примера
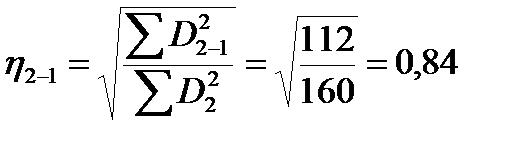 (13.5)
(13.5)
Величина корреляционного отношения не может быть больше единицы и меньше нуля: этот показатель не может быть отрицательным.
Значение 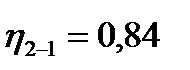 свидетельствует о сильной корреляционной связи второго признака с первым.
свидетельствует о сильной корреляционной связи второго признака с первым.
Может возникнуть вопрос – зачем понадобился новый показатель; нельзя ли в этом случае измерить степень связи при помощи основного показателя – коэффициента корреляции?
Для решения этого вопроса достаточно рассчитать коэффициент корреляции для случая явно криволинейной связи, например, для только что изученной группы из 6 особей (таблица 13.2).
Получился очень малый коэффициент корреляции (r = +0,16), что находится в явном противоречии и с видом корреляционных рядов и с величиной корреляционного отношения. Объясняется это тем, что коэффициент корреляции не может характеризовать степень криволинейной связи.
Таблица 13.2 – Малый коэффициент корреляции при большой криволинейной связи
| X1 | SX1=36 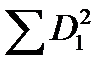 =232–362/6=16 =232–362/6=16
| |||||||
| X2 | SX2=60 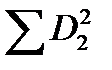 =760–602/6=160 =760–602/6=160
| |||||||
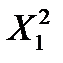
| S 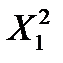 =232 =232
| 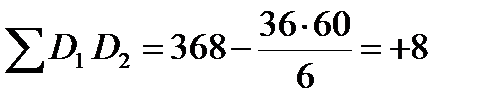
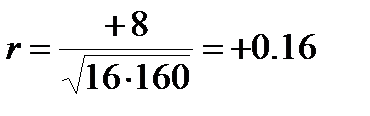
| ||||||
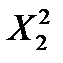
| S 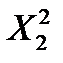 =760 =760
| |||||||
| X1×X2 | SX1×X2=368 |






