Для определения степени приближения криволинейной зависимости к прямолинейной используется критерий F, вычисляемый по формуле:
(13.12)
где:
η2 – квадрат корреляционного отношения Y по Х;
r2 – квадрат коэффициента линейной корреляции;
n – объем выборки;
kx – число групп по ряду X.
Связь можно практически принять за линейную, если
Fфакт < Fтеор, и определять показатели для прямолинейной корреляции и регрессии. Корреляция нелинейная, если Fфакт ≥ Fтеор. Теоретические значения F берутся из таблицы приложений для
ν1 = kx – 2 и ν2 = n – 2 степеней свободы.
Криволинейные зависимости между двумя переменными могут быть выражены в виде кривых линий регрессии и соответствующих им математических уравнений. Эмпирические точки поля регрессии при криволинейной корреляции располагаются около кривых различного типа – парабол, гипербол, логарифмических кривых и т. п.
В общем случае все линии регрессии являются кривыми и рассматриваемая нами ранее линейная регрессия является простейшей зависимостью между двумя признаками.
Основной метод построения математических уравнений: подбор типа формулы и нахождение коэффициента к ней.
Статистическая обработка экспериментального материала часто приводит к полиному второй степени:
(13.13)
Вопросы для самоконтроля
1 Назначение корреляционного отношения. Характеризует ли корреляционное отношение степень криволинейной связи между двумя парными выборками?
2 Дайте определение группового среднего и квадратов отклонений группового варьирования.
3 Напишите формулу, определяющую корреляционное отношение при большом числе наблюдений (>30).
4 В каких пределах заключено значение корреляционного отношения?
5 Что показывает отношение сумм квадратов группового варьирования к общему (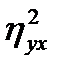
)? Название этого статистического показателя.
6 Одинаковую ли меру связи признаков (первого со вторым и второго с первым) дает коэффициент корреляции и корреляционное отношение?
7 Какой критерий следует брать для определения достоверности и доверительных границ квадрата корреляционного отношения?
8 Что является критерием линейности или нелинейности связи между парными признаками?
9 Какими функциями могут быть аппроксимированы криволинейные зависимости между двумя переменными? Приведите примеры.
ТЕМА 14 Однофакторный дисперсионный анализ
14.1 Сущность и метод дисперсионного анализа
14.2 Однофакторные статистические комплексы
