В уравнении простой прямолинейной регрессии:
у = а + bх
возникают три ошибки репрезентативности.
1 Ошибка коэффициента регрессии:
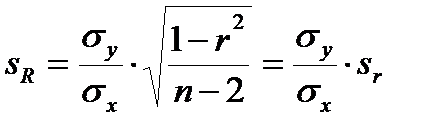(11.20)
2 Ошибка уравнения регрессии, т. е. ошибка средней величины функции для каждого значения аргумента:
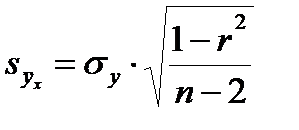(11.21)
По данным вышеприведенного примера:
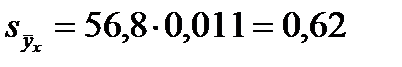
Следовательно, максимальная погрешность в определении уровня точек линии регрессии при первом пороге вероятности безошибочных прогнозов (b1 = 0,95, t1=2,0) будет равна:
D= t ×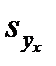 
= 2×0,62 кг = ± 1,24 кг.
3 Ошибка индивидуальных определений функции:
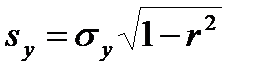(11.22)
Для вышеприведенного примера:
.
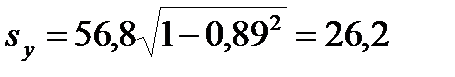Следовательно, индивидуальная погрешность в определении веса лошадей по обхвату груди по найденной формуле регрессии, принимая первый порог вероятности безошибочных прогнозов
(β1 = 0,95, t1 = 2,0), в крайних случаях не будет превышать
D = 2×26 кг = ± 52 кг.
Вопросы для самоконтроля
1 Что такое корреляция?
2 Какая разница между корреляционной и функциональной зависимостями?
3 Какая разница между положительной и отрицательной корреляциями?
4 Коэффициент корреляции как мерило сопряженности в вариации признаков. Его определение с помощью двух нормированных отклонений.
5 В чем заключаются важнейшие свойства среднего произведения двух нормированных отклонений?
6 Напишите общую формулу для вычисления коэффициента корреляции.
7 Что такое корреляционная, решетка? Объясните, как она строится. Можно ли судить о характере корреляции по расположению данных в корреляционной решетке?
8 Каковы возможные значения коэффициента корреляции? Какие значения коэффициента корреляции следует считать высокими, средними и почему?
9 Всегда ли при r = 0 корреляционная связь отсутствует?
10 Чему равен коэффициент корреляции при полной корреляционной связи?
11 Напишите обычную формулу ошибки коэффициента корреляции.
12 Является ли наличие корреляции доказательством причинной зависимости между изучаемыми варьирующими признаками?
13 Напишите формулу достоверности выборочного коэффициента корреляции.
14 Дайте определение доверительных границ коэффициента корреляции.
15 Дайте определение достоверности разности двух коэффициентов корреляции.
16 Что такое регрессия?
17 Под каким углом пересекаются эмпирические линии регрессии при слабой корреляции? При сильной корреляции?
18 Напишите уравнение регрессии в общем виде; в виде уравнения прямой.
19 Напишите систему двух уравнений для определения значений а и b в уравнении у = а + bх.
20 Дайте определение и формализацию коэффициента регрессии.
21 Что выражает уравнение регрессии х по у и уравнение регрессии у по х?
22 Чему равен тангенс угла между линией регрессии и осью х?
23 Может ли коэффициент регрессии быть равным коэффициенту корреляции?
24 Перечислите ошибки элементов уравнения прямолинейной регрессии.
ТЕМА 12 Частная и множественная линейные корреляции и регрессии
12.1 Частный коэффициент корреляции
12.2 Множественный коэффициент корреляции
12.3 Линейное уравнение множественной регрессии
Корреляция называется множественной, если на величину результативного признака одновременно влияют несколько факториальных.
Наиболее простой формой множественной связи является линейная зависимость между тремя признаками, когда один из них, например, урожай, рассматривается как функция (Y), а два другие – как аргументы (X и Z). В качестве меры тесноты линейной связи трех признаков используют частные коэффициенты корреляции, обозначаемые rxy-z, rxz-y, rzy-x и множественные коэффициенты корреляции, обозначаемые символами Rx-yz, Ry-xz, Rz-yx.
