Достоверность разности долей

Достоверность разности выборочных долей определяется так же, как и для разности средних:

(10.34)

где:

t_d – критерий достоверности разности;

d = p₁ – p₂ – разность выборочных долей;

– ошибка разности долей, равная корню квадратному из суммы квадратов ошибок сравниваемых долей.

Если требуется определить только достоверность разности, то квадраты ошибок долей определяются непосредственно:

; ; (10.35)

t_st – стандартное значение критерия определяется так же, как и для разности средних – по таблице стандартных значений критерия Стьюдента или по приближенным формулам, исходя из требуемой вероятности безошибочных прогнозов (b₁ = 0,95, b₂ = 0,99,
b₃ = 0,999) и числа степени свободы разности;

n – число степеней свободы разности, равное сумме объемов сравниваемых выборок n₁ и n₂ без двух.

Пример

При изучении планктона оказалось, что из 8 особей одного вида 7 были самцами, а из 7 экземпляров другого родственного вида самцами были только 2. Можно ли на основании этих данных сделать заключение, что у первого вида доля самцов в данном сезоне выше, чем у второго?

Произведены следующие расчеты:

p₁ = 7/8 = 0,88; ;

p₂ = 2/7 = 0,29; ;

d =0,88 – 0,29 = 0,59; ;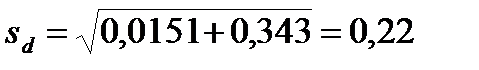

; n = 8 + 7 – 2 = 13; t_st={2,2 – 3,0 – 4,1}.

Оказалось, что разница между видами по относительной доле (%) самцов даже при сравнении долей в таких малых выборках превышает нижний порог достоверности. Поэтому с достаточной для первой ориентировки уверенностью можно заключить, что процент самцов в данном сезоне у первого вида больше, чем у второго.

Пример

При изучении заболеваемости гипертонией выяснено, что от здоровых родителей из 580 сыновей болело 197, а от родителей обоих гипертоников из 39 сыновей болело 28. Можно ли считать, что гипертония поражает сыновей, происходящих от гипертоников, чаще, чем сыновей от здоровых родителей не только среди обследованных сыновей, но и вообще среди всех мужчин?

p₁ = 197/580 =0,34; ;

p₂ = 28/39 = 0,72; ;

d = 0,72 – 0,34 = 0,38; ;

; n = 580 + 39 – 2 = 617; t_st = {2,0 – 2,6 – 3,3}.

Разность оказалась в высшей степени достоверной. Сыновья гипертоников вообще явно чаще болеют гипертонией по сравнению с сыновьями от обоих здоровых родителей.

 

Вопросы для самоконтроля

 

1 Какие три величины необходимы для оценки генерального параметра?

2 Перечислите три основных порога вероятности безошибочных прогнозов.

3 Укажите значения критериев надежности для основных порогов вероятности безошибочных прогнозов при условии достаточно больших выборок.

4 Напишите формулы ошибок репрезентативности основных выборочных показателей.

5 Какие процедуры необходимо выполнить, чтобы оценить генеральный параметр для количественных признаков в форме доверительных границ? Привести примеры.

6 Как определяется недостоверная и достоверная оценка средней разности?

7 Напишите формулу для определения критерия достоверности разности.

8 Напишите формулу ошибку репрезентативности доли при изучении качественных признаков.

9 Напишите формулу ошибки достоверность разности выборочных долей.

ТЕМА 11 Парная корреляция

11.1 Коэффициент корреляции

11.2 Ошибка коэффициента корреляции

11.3 Уравнение прямолинейной регрессии. Коэффициент прямолинейной регрессии

11.4 Ошибки элементов уравнения прямолинейной регрессии

Коэффициент корреляции

Во многих исследованиях требуется изучить несколько признаков в их взаимной связи. Если вести такое исследование по отношению к двум признакам, то можно заметить, что изменчивость одного признака находится в некотором соответствии с изменчивостью другого.

В некоторых случаях такая зависимость проявляется настолько сильно, что при изменении первого признака на определенную величину всегда изменяется и второй признак на определенную величину, поэтому каждому значению первого признака всегда соответствует совершенно определенное, единственное значение второго признака. Такие связи называются функциональными.

Встречаются функциональные связи в физических и математических обобщениях. Площадь треугольника точно определяется его высотой и основанием, длина окружности – радиусом, скорость падения есть функция времени падения и ускорения силы тяжести, скорость протекания определенной химической реакции находится в зависимости от температуры.

Необходимо учесть, что функциональные связи встречаются только в идеальных условиях, когда предполагается, что никаких посторонних влияний нет.

При изучении живых объектов – диких и культурных растений, животных, микроорганизмов – приходится иметь дело со связями другого рода. Живой организм развивается в связи с условиями его жизни, под действием бесконечно большого числа факторов, которые по-разному определяют развитие разных признаков.

У живых объектов связь между любыми двумя признаками настолько часто и сильно нарушается и модифицируется, что не всегда даже может быть легко обнаружена. У растений, животных и микроорганизмов связь между признаками обычно проявляется особым образом. Каждому определенному значению первого признака соответствует не одно значение второго признака, а целое распределение этих значений при вполне определенных основных показателях этого частного распределения – средней величины и степени разнообразия. Такая связь называется корреляционной связью или просто корреляцией.

Корреляционная связь, например, между весом животных и их длиной выражается в том, что каждому значению длины соответствует определенное распределение веса (а не одно значение веса), и с увеличением длины увеличивается и средний вес животных.

Корреляционная связь не является точной зависимостью одного признака от другого, поэтому она может иметь различную степень – от полной независимости до очень сильной связи. Кроме того, характер связи между разными признаками может быть различен. Поэтому возникла необходимость определять форму, направление и степень корреляционных связей.

По форме корреляция может быть прямолинейной и криволинейной, по направлению – прямой и обратной. Степень корреляции измеряется различными показателями, введенными для установления силы связи между количественными и качественными признаками. Такими показателями являются коэффициент корреляции r, корреляционное отношение η.

Изобразить корреляционную связь двух признаков можно тремя способами:

- При помощи корреляционного ряда, состоящего из ряда пар значений, из которых одно относится к первому признаку, а другое в этой паре относится ко второму признаку, связанному с первым. На рисунке 11.1 показаны схемы корреляционных рядов при пяти степенях корреляционной связи.

- При помощи корреляционной решетки, в которой каждой особи соответствует определенная клетка. На рисунке 11.1 показана схема корреляционных решеток для пяти степеней корреляционной связи между двумя признаками. Значения первого признака нанесены по оси абсцисс, значения второго – по оси ординат.

- При помощи линии регрессии, абсциссы которой пропорциональны значениям первого признака, а ординаты – значениям второго признака, корреляционно связанного с первым. На рисунке 11.1 показаны схемы линий регрессии для пяти степеней корреляционной связи между двумя признаками.

 

	X1           X2           Прямая полная связь; r = +1,0
	X1           X2           Прямая частичная связь; r = +0,8
	X1           X2           Отсутствие связи; r = 0
	X1           X2           Обратная частичная связь; r= – 0,8
	X1           X2           Обратная полная связь; r= – 1,0

Рисунок 11.1 – Схема прямолинейных корреляционных связей

Коэффициент корреляции измеряет степень и определяет направление прямолинейных связей.

Прямолинейная связь между признаками – это такая связь, при которой равномерным изменениям первого признака соответствуют равномерные (в среднем) изменения второго признака при незначительных и беспорядочных отклонениях от этой равномерности. Например, при увеличении длины тела на каждый сантиметр ширина увеличивается в среднем на 0,7 см.

При графическом изображении прямолинейных связей
(рисунок 11.1) (если по оси абсцисс отложить значения первого признака, по оси ординат – второго и полученные точки соединить) получается прямая или такая кривая, среднее которой проходит по прямой.

При изображении прямолинейных корреляционных связей в форме корреляционных решеток (рисунок 11.1) частоты внутри располагаются в форме эллипса. Большая ось этого эллипса проходит или по диагонали от угла наименьших значений (при положительной корреляционной связи), или по диагонали от угла, где сходятся наименьшие значения одного признака и наибольшие значения другого, к противоположному углу (при отрицательной корреляционной связи).

При измерении степени связи между разными признаками приходится сравнивать величины, выраженные в разных единицах измерения. Например, при измерении связи между весом животного и его длиной надо сопоставить килограммы веса с сантиметрами длины. В других случаях изменения объема сопоставляются с изменениями возраста, изменения веса руна в килограммах с изменениями содержания в нем жиропота в процентах, длина ног в сантиметрах со скоростью бега в минутах и т. д.

Проводить такие сравнения оказалось возможным путем использования нормированного отклонения, вычисляемого по формуле:

(11.1)

Нормированное отклонение служит универсальной и неименованной мерой развития признаков. Эти свойства нормированного отклонения и позволили сконструировать основной показатель корреляционной связи – коэффициент корреляции.

Основная формула, которая вскрывает сущность этого показателя, имеет совсем простую структуру:

(11.2)

где r – коэффициент корреляции;

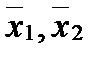– нормированные отклонения данных по первому и второму признаку;

n – число степеней свободы, равное в данном случае числу сравниваемых пар без одной.

Сумма произведений нормированных отклонений, входящая в формулу для коэффициента корреляции, обладает следующими тремя особыми свойствами.

Если оба признака изменяются параллельно, то сумма произведений их нормированных отклонений дает положительную величину. Если при увеличении одного признака другой уменьшается, то приходится умножать положительные числа на отрицательные и вся сумма произведений нормированных отклонений дает отрицательную величину. Поэтому коэффициент корреляции может определять направление связи: при прямых связях он положителен, а при обратных связях отрицателен.

При полных связях, когда изменения обоих признаков строго соответствуют друг другу и корреляционная связь превращается в функциональную, сумма произведений нормированных отклонений становится равной числу степеней свободы:

(11.3)

Поэтому максимальное значение коэффициента корреляции равно 1 для положительных или прямых связей:

(11.4)

для отрицательных, или обратных связей:

(11.5)

При полном отсутствии корреляционной связи между признаками сумма произведений нормированных отклонений равна нулю, и поэтому коэффициент корреляции в этих случаях тоже равен нулю:

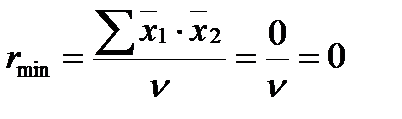(11.6)

Предельные значения коэффициента корреляции (r =+1,0; r =0,0;
r = –1,0) на практике встречаются крайне редко.

Пять основных видов прямолинейной корреляционной связи, соответствующие коэффициентам корреляции +1,0; +0,8; 0,0; –0,8 и
–1,0, показаны на рисунке 11.1.

Основная формула коэффициента корреляции хорошо вскрывает сущность этого показателя, но для работы крайне неудобна, особенно при многочисленных группах. Поэтому разработаны разнообразные рабочие формулы для практических расчетов в разных условиях – для малых и больших групп при малозначных и многозначных вариантах.

Все эти формулы дают одинаковый результат и применение любой из них обусловливается только удобством и простотой необходимых вычислений.

В биологических работах наиболее приемлема формула, предложенная для малых групп:

, (7.6)

где:

X₁, X₂ – данные первого и второго признаков;

N – число сравниваемых пар данных, или число объектов, у которых измерено по два признака;

σ₁, σ₂ – стандартные отклонения по первому и по второму признаку.

Применяется коэффициент корреляции в тех случаях, когда необходимо знать направление и силу связи между признаками, причем заранее известно, что эта связь может считаться прямолинейной, или когда требуется выяснить степень именно прямолинейной связи. При этом лучше проводить два этапа исследования:

1 рассмотрение графика поля регрессии;

2 расчет коэффициента корреляции непосредственно по данным.

Уже самый вид графика позволяет установить направление и степень прямолинейных связей, а также характер криволинейных связей. При известном опыте по виду графика можно получить первое представление об особенностях и силе связи между изучаемыми признаками.