Определение 17. Выборочное среднее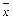 
– среднее арифметическое значение признака выборочной совокупности
.
Определение 18. Выборочной дисперсией D называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения :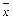
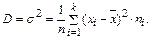
Дисперсию можно рассчитать по формуле:
Определение 19. Выборочным средним квадратическим отклонением называется величина 
характеризующая отклонение, разброс в линейных размерах данных выборки относительно выборочного среднего.
Точечные оценки
Определение 20. Статистической оценкой неизвестного параметра генеральной совокупности называется приближенное значение, полученное по данным выборки.
Определение 21. Точечная оценка – оценка, которая определяется одним числом q. Это точка на числовой оси, около которой находится оцениваемый параметр генеральной совокупности q 0.
Определение 23. Оценка q параметра q 0 называется состоятельной, если для любого положительного d 
, то есть q стремится к q 0 по вероятности и означает неограниченное увеличение точности с ростом объема выборки.
Определение 24. Оценка q параметра q 0 называется эффективной, если она является несмещенной и имеет наименьшую дисперсию при заданном объеме выборки.
Теорема 5. Выборочное среднее – несмещенная, состоятельная и эффективная оценка математического ожидания признака генеральной совокупности.
Теорема 6. Дисперсия выборочного среднего в n раз меньше дисперсии генеральной совокупности:
.
Теорема 7. Математическое ожидание выборочной дисперсии рассчитывается по формуле
.
Следовательно, дисперсия выборочного среднего является смещенной оценкой генеральной дисперсии. Чтобы получить несмещенную оценку вводится исправленная дисперсия:
.
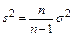Интервальные оценки
Определение 25. Интервал (q – d, q + d), в пределах которого с вероятностью g находится оцениваемый параметр генеральной совокупности q 0, называется доверительным интервалом. Значение g называется доверительной вероятностью или надежностью оценки; предельная погрешность d – точность оценки.
Доверительный интервал для оценки математического ожидания нормального распределения определяется следующим образом:
причем, если стандартное отклонение этого распределения известно, то
;
Здесь число t определяется из равенства F (t) = g / 2; tg находится по таблице коэффициентов Стьюдента при заданных n и g (таблица № 4 Приложений); s – исправленное выборочное среднее квадратическое отклонение.
Интервальной оценкой (с надежностью g) стандартного отклонения s 0 нормально распределенного количественного признака X по исправленному выборочному стандартному отклонению s служит доверительный интервал
s ×(1 – q) < s 0 < s ×(1 + q) при q < 1,
0 < s 0 < s ×(1 + q) при q > 1,
где q = q (n;g) определяется по таблице № 5 Приложений.
Задача. По данным выборки найти доверительные интервалы для оценок с надежностью g = 0,95 неизвестных математического ожидания a и стандартного отклонения s нормально распределенного признака X генеральной совокупности. Построить полигон частот по данным выборки:
| xi | –2 | |||||
| ni |
Решение.
1) Найдем объем выборки
.
2) Найдем выборочную среднюю
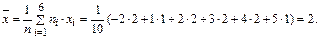
3) Вычислим дисперсию
4) Вычислим «исправленную» дисперсию и «исправленное» стандартное отклонение
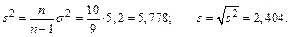
5)
