Неравенства Маркова и Чебышева в условиях схемы Бернулли

Здесь М(X) = np и D (X) = npq. Тогда неравенство Маркова записывается как:

- первая форма неравенства;

- вторая форма неравенства.

С учетом дисперсии:

А неравенство Чебышева принимает вид:

- первая форма неравенства;

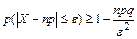- вторая форма неравенства.

Если в задаче отсутствует информация о вероятностях p и q, то необходимо воспользоваться ограничением pq £ 0,25.

Задача 1. Среднее число телевизоров, получаемых ремонтной мастерской в течение недели, равно 10 со средним квадратическим отклонением 3. Оценить вероятность того, что в предстоящую неделю в мастерскую поступит не более 25 телевизоров.

Решение. Случайная величина X – число телевизоров, получаемых ремонтной мастерской в течение недели.

Нанесем данные задачи на числовую прямую:

10 15

0 а= 10 25

Итак, границы интервала заданного изменения Х несимметричны относительно математического ожидания, следовательно, для решения задачи применяется неравенство Маркова (вторая форма в (16)):

С другой стороны, известно среднее квадратическое отклонение s = 3, а тогда D (X) = s ² = 9. Используем неравенство Маркова при известной дисперсии:

Сравнивая полученные результаты, делаем вывод: p (X £ 25) ³ 0,8256.

Ответ: p (X £ 25) ³ 0,8256.

Задача 2. Завод отгрузил реализатору 5000 бутылок пива. Вероятность боя стеклотары в пути и при погрузочно-разгрузочных работах в целом

2. Составим вспомогательную таблицу для условных вариант с учетом: n_u = n_x; n_v = n_y; n_uv = n_xy. В углах клеток с n_uv ¹ 0 укажем отличные от 0 произведения соответствующих вариант u_i × v_j.

U / V	–3	–2	–1	n_u
–2	6
–1

			–1

n_v				n =50

3. Находим средние арифметические условных вариант:

и, следовательно,

4. Находим средние арифметические квадратов условных вариант:

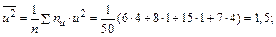
И, следовательно, с требуемой точностью среднеквадратичные отклонения условных вариант:

5. Находим среднее арифметическое произведения условных вариант

, суммируя произведения значений

в углах клеток вспомогательной таблицы на соответствующие частоты

в этих клетках:

ления достаточно оставлять не более трех значащих цифр после запятой; результирующее значение r округлить до сотых.

3. При выводе заключения о тесноте линейной корреляционной связи между Y и X предполагается придерживаться следующей градации:

- если r = 0, то между X и Y линейная корреляционная связь отсутствует (при этом не исключена другая форма корреляционной связи);

- если 0 < | r | £ 0,6, то между X и Y линейная корреляционная связь слабая;

- если 0,6 < | r | £ 0,8, то между X и Y линейная корреляционная связь тесная;

- если 0,8 < | r | < 1, то между X и Y линейная корреляционная связь очень тесная;

- если , то между X и Y линейная корреляционная связь функциональная.

Задача. В нескольких одинаковых отрезках проволоки исследуется взаимозависимость силы тока Y и температуры X при заданном напряжении. Полученные значения случайных переменных X и Y в условных единицах сведены в корреляционную таблицу

X / Y							n_x
1,5

2,5

3,5
n_y							n =50

Найти выборочное линейное уравнение регрессии Y на X, выборочный коэффициент корреляции и сделать вывод о тесноте линейной корреляционной связи между X и Y.

Решение.

1. Значения как X, так и Y заданы в таблице равноотстоящими, поэтому перейдем к условным вариантам: где учтено, что шаги h ₁ = 0,5; h ₂ = 20, а максимальной частоте n_xy = 10 соответствует пара x * = 2,5; y * = 80.

составляет 0,06. Оценить вероятность того, что число разбитых бутылок у реализатора превзойдет 500.

Решение. Случайная величина X – число разбитых бутылок.

Нанесем данные задачи на числовую прямую:

0 a= 300 500 5000

Математическое ожидание и дисперсия находятся по формулам a = np и D (X) = npq, так как задача относится к задачам на схему Бернулли. Итак, a = 5000×0,06 = 300; D (X) = 5000×0,06×0,94 = 282.

Используем неравенство Маркова в условиях схемы Бернулли:

Сравнивая результаты, делаем вывод: p (X > 500) £ 0,3611.

Ответ: p (X > 500) £ 0,3611.

Задача 3. Среднее число автобусов автопарка, отправляемых в ремонт после месяца эксплуатации, равно 10 при среднем квадратическом отклонении 4 автобуса. Оценить вероятность того, что в течение месяца автопарк отправит в ремонт от 5 до 15 машин включительно.

Решение. Х – число автобусов, отправляемых в ремонт.

Нанесем данные задачи на числовую прямую:

5 5

0 5 a =10 15

Известно, что s = 4, а, следовательно, D (X) = s ² = 16; интересуемый интервал значений Х симметричен относительно математического ожидания этой случайной величины, поэтому воспользуемся неравенством Чебышева (второй формой в (18)):

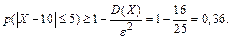
Ответ: p (| X – 10| £ 5) ³ 0,36.

Задача 4. Вероятность задержки рейса самолета по техническим причинам равна 0,03. Оценить вероятность того, что из 1200 планируемых в

течение месяца вылетов из аэропорта произойдет по этим причинам задержка более 72 рейсов.

Решение. X – число задержек вылетов самолетов в месяц.

Нанесем данные задачи на числовую прямую:

36 36

0 a= 36 72 1200

Математическое ожидание и дисперсия находятся по формулам a = np и D (X) = npq, так как задача относится к задачам на схему Бернулли. Итак, a = 1200×0,03 = 36, D (X) = 1200×0,03×0,97 = 34,92.

Дисперсия известна, а также интервал значений случайной величины Х вне искомого имеет границы, симметричные относительно математического ожидания а = 36, следовательно, используем для решения задачи неравенство Чебышева в условиях схемы Бернулли:

p (X > 72) = 1 – p (X £ 72) = 1 – p (| X – 36| £ 36) £ 1 – =

= 34,92/ 36² = 0,0269.

Ответ: p (X > 72) £ 0,0269.