Пусть гипотезы В 1, В 2, …, Вn образуют полную группу событий и попарно несовместны, а событие A может наступить лишь в результате осуществления одной из гипотез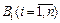 
. Тогда вероятность события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
(2)
где p (В 1) + p (В 2)+…+ p (Вn) = 1.
Допустим, произведено испытание, в результате которого появилось событие А. Вероятности гипотез Вi после опыта, т.е. условные вероятности: р (А/В 1), р (А/В 2 ), …, р (А/Вn), вычисляются по формуле Байеса:
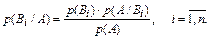(3)
Эта формула позволяет оценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Задача 1. После вакцинирования животное в период эпидемии заболевает с вероятностью 0,01, а не вакцинированное – 0,8. Вакцинировано 70% животных. Найти вероятность того, что во время эпидемии животное заболеет.
Решение. Обозначим событие А = {животное заболеет}. Возможны следующие гипотезы: В 1 = {животное вакцинировано}, В 2 = {животное не вакцинировано}. Гипотезы В 1, В 2 несовместны и образуют полную группу событий. По условию задачи вероятности этих гипотез: р (В 1) = 0,7, р (В 2) = 0,3. Условная вероятность того, что животное заболеет, если оно вакцинировано р (В 1/ А) = 0,01, а условная вероятность того, что животное заболеет, если оно не вакцинировано р (В 2/ А) = 0,8.
Вероятность события А определяется по формуле полной вероятности:
р (А) = р (В 1)· р (В 1/ А) + р (В 2)· р (В 2/ А) = 0,7·0,01 + 0,3·0,8 = 0,247.
Ответ: р (А) = 0,247.
Задача 2. В ящике содержится 12 деталей завода №1, 20 деталей завода №2, 18 деталей завода №3. Завод №1 выпускает 90% продукции отличного качества, завод №2 – 60%, а завод №3 – 80% продукции отличного качества. Извлеченная наудачу из ящика деталь оказалась отличного качества. Найти вероятность того, что она изготовлена на заводе №2.
Решение. Обозначим событие А ={наудачу взятая из ящика деталь окажется отличного качества}. Возможны следующие гипотезы: В 1 = {деталь изготовлена на i -м заводе},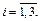 
Гипотезы В 1, В 2, В 3 попарно несовместны и образуют полную группу событий. Поскольку в ящике всего 22+20+18 = 50 деталей, то по классической формуле вероятности:
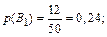
9.5.
| X \ Y | nx | |||||||
| - | - | - | - | - | ||||
| - | - | - | - | - | ||||
| - | - | - | ||||||
| - | - | - | - | |||||
| - | - | - | ||||||
| ny | n =100 |
9.6.
| X \ Y | nx | |||||||
| - | - | - | - | - | ||||
| - | - | - | - | - | ||||
| - | - | - | - | |||||
| - | - | - | ||||||
| - | - | - | ||||||
| ny | n =100 |
9.7.
| X \ Y | nx | |||||||
| - | - | - | - | - | ||||
| - | - | - | ||||||
| - | - | |||||||
| - | - | - | ||||||
| - | - | - | - | - | ||||
| ny | n =50 |
9.8.
| X \ Y | nx | |||||||
| - | - | - | - | |||||
| - | - | |||||||
| - | - | - | ||||||
| - | - | |||||||
| - | - | - | - | - | ||||
| ny | n =100 |
9.9.
| X \ Y | nx | |||||||||
| - | - | - | ||||||||
| - | - | - | ||||||||
| - | ||||||||||
| - | - | - | ||||||||
| - | - | |||||||||
| ny |
Задача 9. Линии регрессии.
Найти выборочное уравнение прямой линии регрессии Y на X по данным, приведенным в корреляционной таблице.
9.1.
| X \ Y | nx | |||||||
| - | - | - | - | - | ||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | ||||||
| - | - | - | - | - | - | |||
| ny | n =50 |
9.2.
| X \ Y | nx | |||||||
| - | - | - | - | - | - | |||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| ny | n =50 |
9.3.
| X \ Y | nx | |||||||
| - | - | - | - | - | ||||
| - | - | - | - | - | ||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| ny | n =50 |
9.4.
| X \ Y | nx | |||||||
| - | - | - | - | |||||
| - | - | |||||||
| - | - | - | ||||||
| - | - | |||||||
| - | - | - | - | - | ||||
| ny | n =100 |
Условные вероятности того, что деталь окажется отличного качества, если она изготовлена на i -м заводе (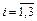
) по условию задачи равны: 
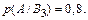
По формуле полной вероятности (2):
р (А) = 0,24∙0,9 + 0,4∙0,6 + 0,36∙0,8 = 0,744.
По формуле Байеса (3) найдем вероятность того, что извлеченная деталь изготовлена на заводе №2:
Ответ: р (В 2 / А) = 0,323.
III. Схема Бернулли
