Алгоритм 2. Расстановка меток у вершин графа игры

1. Инициализация. Сопоставим финальной вершине метку 0.

В поочерёдных позиционных играх, в которых ноль стоит в финальной позиции, все остальные нули и единицы ставятся по следующим правилам:

А. Пометим 1-ей все вершины, откуда за один ход можно попасть в вершины с меткой 0.

Б. Пометим 0-ём все вершины, откуда за один ход можно попасть только в вершины с меткой 1.

В. Чередуем шаги А и Б до тех пор, пока не окажется помеченной начальная вершина.

Стоп (алгоритм прекращает работу).

Дадим необходимые пояснения. Тот игрок, который каким бы то ни было образом оказал-ся в вершине с меткой 1, может гарантированно выиграть, потому что он всегда может из 1 пе-рейти в 0, откуда другой игрок может перейти только в 1 и т.д. Таким образом, другой игрок всегда будет попадать в вершины с меткой 1, и поэтому он никогда не придёт в финальную вершину с меткой 0. Следовательно, если в начальной вершине стоит метка 1, то начинающий игрок выигрывает, а если стоит 0, то он проигрывает ■

Пример 9. Рассмотрим игру из примера 8 и проиллюстрируем на этом примере работу ал-горитма 2. Прежде всего надо добавить новую финальную вершину z, поскольку в исходной иг-ре из примера 8 игрок, попавший в финальную вершину, проигрывает. Новый граф показан на рисунке 9a. У вершины z, в соответствии с шагом 1 алгоритма 2, поставлена метка 0.

Выполняя шаг А, ставим метку 1 у вершины (0,0), откуда можно попасть в вершину z, у которой уже стоит метка 1 (см. рис.9b). Выполняя шаг 2, ставим метки 0 у вершин (0,1) и (1,0), откуда можно попасть только в вершину (0,0), у которой уже стоит метка 1 (см. рис.9c). Далее, выполняя 2-ой раз шаг А, ставим метку 1 у 5 вершин: (0,2), (1,2), (1,1), (2,1), (2,0), из каждой из которых можно попасть в вершины (0,1) или (1,0), уже помеченных 0-ём (рис.9d). Выполняя 2-ой раз шаг Б, ставим метку 0 у вершин (0,3), (2,2) и (3,0), из которых можно попасть только в одну из вершин (0,2), (1,2), (1,1), (2,1), (2,0), которые уже получили метку 1 (рис.9e).

Дальнейшие аналогичные шаги представлены на рис.9fи 9g, а затем на рис.9h и 9i. При выполнении шага Б начальная вершина (4,4) получает метку 0. Это означает, что начинающий игрок в данной игре проигрывает, если другой игрок будет каждый раз из вершины с меткой 1 переходить в вершину с меткой 0, в соответствии с пояснениями к алгоритму 2.

 

Рис.9a. Новый граф и его инициализация

 

Рис.9b. Шаг А-1

Рис.9c. Шаг Б-1

 

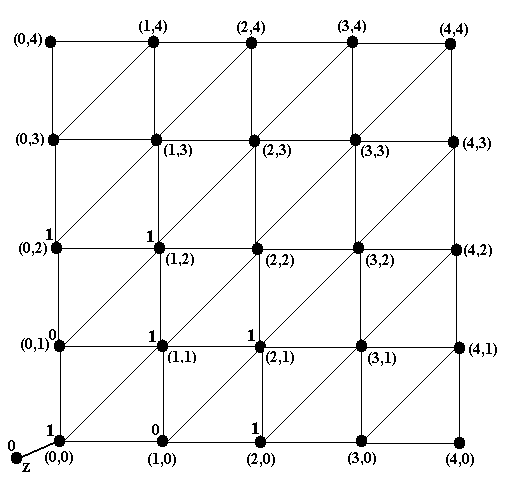Рис.9d. Шаг А-2

Рис.9e. Шаг Б-2

 

 

Рис.9f. Шаг А-3

Рис.9g. Шаг Б-3

 

Рис.9h. Шаг А-4

Рис.9i. Шаг Б-4

■

Пример 10. Рассмотрим модификацию игру «Две кучки» с графом на рис.10. От игры из

Рис.10. Граф модифицированной игры «Две кучки»

 

из примеров 8 и 9 она отличается только тем, что игрок, взявший последнюю фишку, выигрыва-ет. Это означает, что вершина (0,0) является финальной вершиной и в соответствии с шагом 1 алгоритма 2 она получает метку 0. Все метки, поставленные в соответствии с алгоритмом 2, показаны на рис.10. У всех вершин, кроме самого левого столбца и самой нижней строки, все метки на рисунках 10 и 9i полностью совпадают. В частности, совпадают и метки у начальной вершины (в обоих случаях 0). Поэтому в модифицированной игре «Две кучки» начинающий также проигрывает, как и в исходной игре. Это означает, что симметрия при изменении опреде-ления победителя отсутствует ■

Задание 3. Найти решение в играх «Две кучки», заданных в следующей таблице:

№	Число фи-шек в 1-ой кучке	Число фи-шек во 2-ой кучке	Игрок, взявший последнюю фишку
			проигрывает
			выигрывает
			проигрывает
			выигрывает
			проигрывает
			выигрывает
			проигрывает
			выигрывает
			проигрывает
			выигрывает
			проигрывает
			выигрывает
			проигрывает
			выигрывает
			проигрывает
			выигрывает

Ответ должен быть дан в виде графа с помеченными вершинами, как на рис.9i и 10. Должно быть указано, какой игрок (начинающий или следующий) выигрывает ■

 

Предметный указатель

 

график игрока

игр биматричных, смешанное расширение

игра Аумана

игра «две кучки»,

модифицированная

игра «ним»

игра «семейный спор»

игры биматричные

игры биматричные

размерности 2×2

игры позиционные

игры, позиция

начальная

финальная

платёжная матрица

игрока A

игрока В

равновесие Нэша

в смешанных стратегиях

в чистых стратегиях

равновесий Нэша нахождение

стратегия

смешанная оптимальная

игрока A

игрока В

чистая оптимальная

игрока A

игрока В